МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

Федеральное государственное автономное образовательное учреждение высшего образования

«НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ ТОМСКИЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИСТЕТ»

Инженерной школы энергетики

Отделение электроэнергетики и электротехники

Лабораторная работа №12

ИССЛЕДОВАНИЕ ПЕРЕХОДНЫХ ПРОЦЕССОВ В ЦЕПЯХ ПЕРВОГО ПОРЯДКА

Вариант 8

Исполнитель:
студент группы	5А8Д		Нагорнов А.В.
Руководитель:
к.т.н., доцент ОЭЭ ИШЭ			Колчанова В. А.

Томск 2020

Цель работы. Исследование переходных процессов в цепях с конденсатором, характеризующихся дифференциальными уравнениями первого порядка.

Схемы электрических цепей

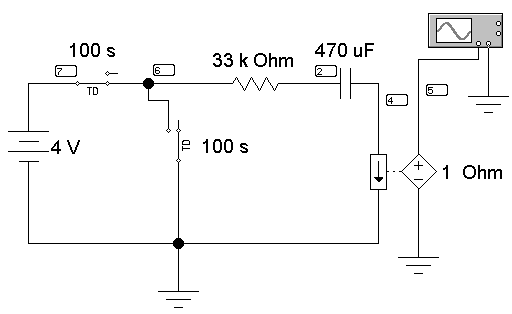
Рис. 12.2.

Таблица 12.1

Вариант		1	2	3	4	5	6	7	8	9	10
U	В	10	11	12	13	14	3	4	4	5	6
R	кОм	100	122	133	147	200	22	22	33	33	47
C	мкФ	100	100	100	100	100	470	470	470	470	470

Подготовка к работе

(ответы на вопросы)

1. Физическая причина возникновения переходных процессов в цепях — наличие в них катушек индуктивности и конденсаторов, то есть индуктивных и ёмкостных элементов в соответствующих схемах замещения.

2. Первый закон коммутации. Ток и магнитный поток в индуктивности непосредственно после коммутации равны току и магнитному потоку в той же индуктивности непосредственно перед коммутацией, а затем плавно изменяется.

Второй закон коммутации. Напряжение и заряд на емкости непосредственно после коммутации равны напряжению и заряду на этой же емкости непосредственно перед коммутацией, а затем плавно изменится.

3. Решение задачи по расчету переходного процесса сводится к нахождению функций времени (обычно i(t) или u(t)), удовлетворяющих системе уравнений Кирхгофа в переходном режиме.

Если после коммутации в цепи действуют постоянные источники, принужденный режим является стационарным. Принужденную составляющую находим методами расчета стационарных режимов.

При синусоидальной форме источников, действующих в послекоммутациной схеме, для определения принужденных токов и напряжений целесообразно воспользоваться символическим методом.

4. Чтобы найти постоянную интегрирования в переходном процессе классическим методом, необходимо вычислить разность тока или напряжения в первый момент после коммутации и соответствующей принуждённой составляющей.

5. Обратное отношение 1/p, измеряемое в секундах, определяет скорость переходного процесса и называется постоянной времени. Постоянная времени для цепи первого порядка с одной емкостью вычисляется как произведение емкости С и некоторого эквивалентного сопротивления. Это эквивалентное сопротивление находится как входное сопротивление цепи со стороны реактивности.

6. В исследуемой цепи постоянная времени . В цепи RL постоянная времени .

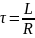7. Выведем формулы для расчёта тока и напряжения при разряде конденсатора.

,

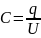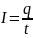
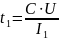– время заряда конденсатора.

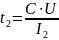– по истечении этого времени конденсатор разрядится до нуля.

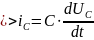– формула показывает, что напряжение на конденсаторе при его заряде не сразу достигает своего максимального значения

При замыкании ключа, заряженный конденсатор С, обладающий энергией 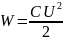, начинает разряжаться, т.е. в цепи появляется разрядный ток.

Согласно закону Ома, мгновенное значение силы тока через сопротивление при разрядке конденсатора равно .

Поскольку заряд конденсатора при разрядке уменьшается с течением времени, то .

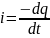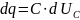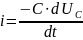Так как , то получим . Отсюда .

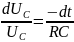Интегрируя полученное выражение с учетом того, что при t=0, Uc = U, имеем:

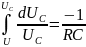
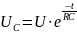
Поэтому разрядный ток будет определяться по закону

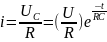
8. По закону Ома .
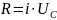