Лабораторная №14

МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

Федеральное государственное автономное образовательное учреждение высшего образования

«НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ ТОМСКИЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИСТЕТ»

Инженерной школы энергетики

Отделение электроэнергетики и электротехники

Лабораторная работа №14

АПЕРИОДИЧЕСКИЙ ПРОЦЕСС В ЦЕПИ ВТОРОГО ПОРЯДКА

Вариант 8

Исполнитель:
студент группы			Нагорнов А.В.
Руководитель:
к.т.н., доцент ОЭЭ ИШЭ			Колчанова В. А.

Томск 2020

Цель работы: Исследовать переходный процесс в активно-ёмкостной цепи с двумя конденсаторами.

Схемы электрических цепей

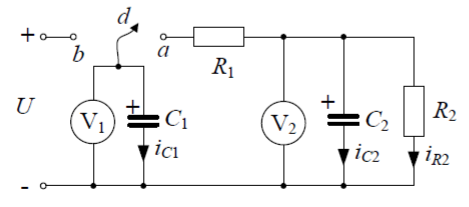
Рисунок 1

Таблица 1

Вариант		8
U	В	11
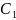
	мкФ	470
	мкФ	100
	кОм	80
	кОм	100

Подготовка к работе:

1. Цепью второго порядка называется цепь, содержащая одновременно индуктивные и ёмкостные элементы. Апериодический переходный процесс возможен только в цепях второго порядка с отрицательными действительными и не равными корнями.

2. Характеристическое уравнение составляется для цепи после коммутации. Оно может быть получено путем использования выражения для входного сопротивления цепи на синусоидальном токе или путем исключения из системы уравнений, описывающих электромагнитное состояние цепи на основании первого и второго законов Кирхгофа, всех неизвестных величин, кроме одной, относительно которой и записывается уравнение.

Для возникновения апериодического процесса корни должны быть действительные, отрицательные и не равные.

3. Принуждённые составляющие для этой цепи равны нулю, т.к. на конденсаторе возникает разрыв.

4. Уравнения выведены в ходе выполнения лабораторной ниже.

Выполнение лабораторной работы:

1. Проведём эксперимент и запишем экспериментальные данные в таблицу 2.

Таблица 2

t	U = 11 B		C1 = 470 мкФ			C2 = 100 мкФ		R1 = 80 кОм		R2 = 100 кОм
	Эксперимент uC1 uC2 (из экспериментальных кривых) iC1 iC2 iR2 – расчётные точки.							Расчет
	uC1	uC2		iC1	iC2		iR2		uC1		uC2
c	В	В		мкА	мкА		мкА		В		В
0 5 10 15 20 40 80 120 160 200	11 10 9.3 8.74 8.25 6.65 4.26 2.73 1.76 1.13	0 3.7 4.8 4.93 4.78 3.84 2.48 1.6 1.02 0.66		-135.7 -78.75 -56.25 -47.63 -43.37 -35.13 -22.25 -14.12 -9.25 -5.87	135.7 41.75 8.25 -1.67 -4.42 -3.27 -2.55 -1.87 -0.95 -0.72		0 37 48 49.3 47.8 38.4 24.8 16 10.2 6.6		10.856 10 9.3 8.74 8.25 6.65 4.26 2.73 1.76 1.13		0 3.7 4.8 4.93 4.78 3.84 2.48 1.6 1.02 0.66

2. Находим токи после коммутации методом контурных токов.

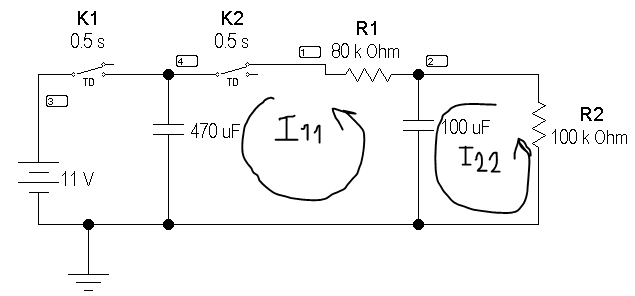
Рисунок 2

=> , ,

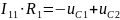
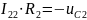
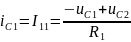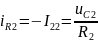
Пример расчёта:

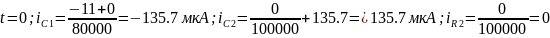
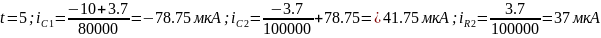
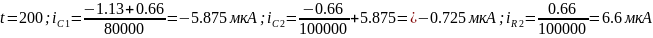
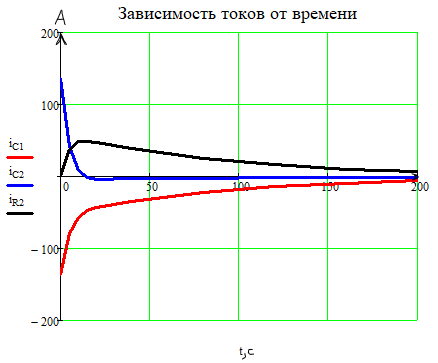
Рисунок 3

3. Выведем уравнения для расчёта напряжений на конденсаторах после коммутации по законам Кирхгофа.

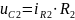
Приведём пример расчёта:

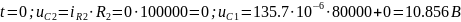
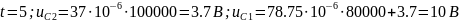
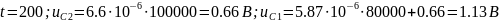
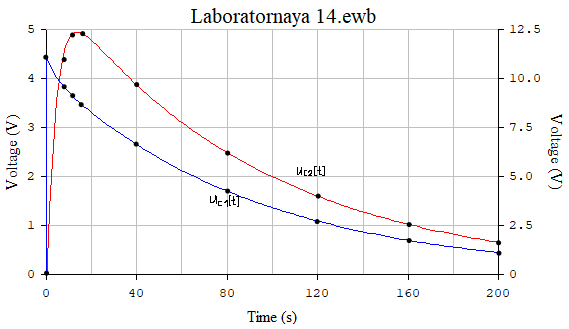
Рисунок 4

Вывод: Благодаря высокой точности данных осциллографа EWB, расчётные и экспериментальные значения токов и напряжений в цепи во времени получились равны. В данной активно-ёмкостной цепи с двумя конденсаторами возникает апериодический переходный процесс, т.к. корни характеристического уравнения действительные, отрицательные и разные.

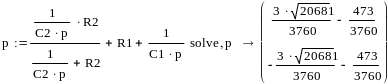
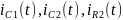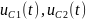Токи и напряжения убывают в течении времени, т.к. контакт с источником тока разомкнут.