
ПРИМЕР_ЛР_Уравнение Д.Бернулли (1)
.pdf
ПРИМЕР выполнения (06/04/2020) |
Стр. 1 |
Лабораторная работа «Уравнение Даниила Бернулли» |
|
ЛАБОРАТОРНАЯ РАБОТА
«УРАВНЕНИЕ ДАНИИЛА БЕРНУЛЛИ»
НА ПРИМЕРЕ ТРУБОПРОВОДА ПЕРЕМЕННОГО СЕЧЕНИЯ ПРИ УСТАНОВИВШЕМСЯ ДВИЖЕНИИ
Цель работы:
1)Ознакомиться с энергетическим смыслом уравнения Д. Бернулли
2)Ознакомиться с геометрическим смыслом уравнения Д. Бернулли и его графическим изображением
3)Провести анализ уравнения Д. Бернулли на примере трубопровода переменного сечения.
4)Построить напорную и пьезометрическую линии для трубопровода переменного сечения.
Схема лабораторной установки.
В данной лабораторной работе уравнение Даниила Бернулли
|
|
|
|
2 |
|
|
|
2 |
|
|
+ |
1 |
+ |
1 |
1 |
= + |
2 |
+ |
2 |
2 |
+ |
|
|
|
|
|
|
|||||
1 |
|
|
2 |
2 |
|
2 |
|
|||
|
|
|
|
|||||||
анализируется применительно к напорному трубопроводу переменного поперечного сечения (на рис.1). Трубопровод расположен горизонтально.
Схема данной установки представлена на рис.2.
Рис.1. Лабораторная установка трубопровода переменного сечения
ПРИМЕР выполнения (06/04/2020) |
Стр. 2 |
Лабораторная работа «Уравнение Даниила Бернулли» |
|
Рис.2. Схема трубопровода переменного сечения
На трубопроводе обозначены пять живых сечений, между которыми расположены характерные участки трубопровода:
1-2 – прямой участок трубы постоянного диаметра; 2-3 – плавное сужение трубы; 3-4 – плавное расширение трубы;
4-5 – прямой участок трубы постоянного диаметра.
Выполнение лабораторной работы
На уровне оси трубопровода в намеченных живых сечениях 1-5 присоединены пять стеклянных прозрачных пьезометров. Изначально трубопровод заполнен водой с некоторым избыточным давлением. При закрытом выходном кране вода в трубопроводе неподвижна и подчиняется законам гидростатики. Поэтому уровни воды во всех пьезометрах находятся на одной отметке.
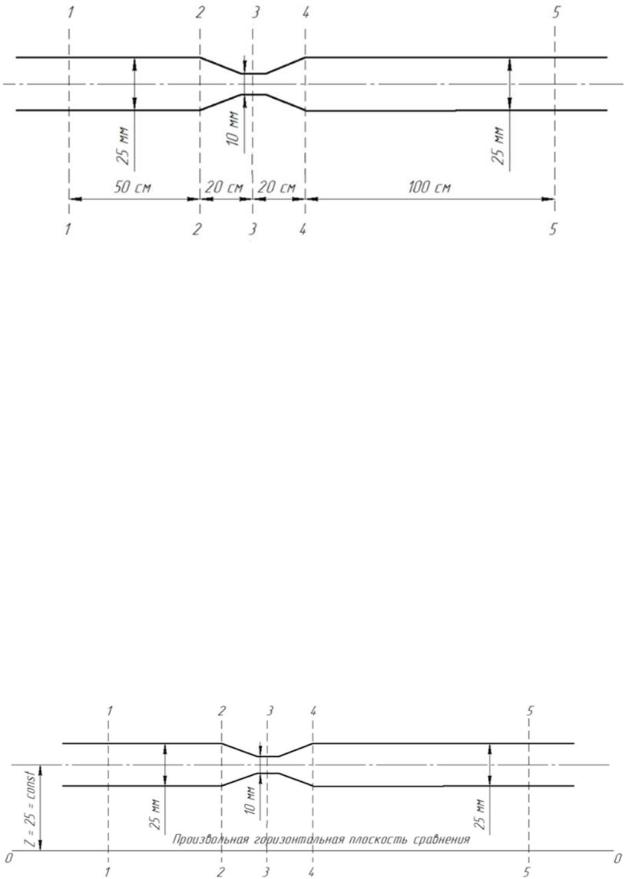
При помощи линейки определяется геометрическая высота Z (см.рис.3) от заданной произвольной горизонтальной плоскости сравнения 0-0 до оси горизонтального трубопровода переменного сечения. Для данного опыта она будет одинакова для всех живых сечений: Z = 25 см = const.
Рис.3. Определение геометрической высоты для трубопровода

ПРИМЕР выполнения (06/04/2020) |
Стр. 3 |
Лабораторная работа «Уравнение Даниила Бернулли» |
|
После открытия выходного крана вода приходит в движение и уровни воды в пьезометрах устанавливаются в соответствии с законами гидродинамики (см.рис.4). Значения пьезометрических высот записываются в соответствующие графы таблицы 1.
Рис.4. Пьезометрические высоты в установке трубопровода переменного сечения
Рис.5. Пьезометрические высоты на схеме трубопровода переменного сечения
Далее, при помощи секундомера засекается время прохождения заданного объёма воды W = 10 л через расходомер, который установлен на трубопроводе. Время составило 40 секунд.
ПРИМЕР выполнения (06/04/2020) |
Стр. 4 |
Лабораторная работа «Уравнение Даниила Бернулли» |
|
Обработка лабораторной работы
1) Вычисляется расход воды: = = 1040000 = 250 см3⁄с
где W – объём воды, прошедший через расходомер, см3 (1 л = 103 см3);
t – время, за которое заданный объём воды прошёл через расходомер (t=40 с). 2) Вычисляются средние скорости V движения воды в заданных живых
сечениях, где установлены пьезометры:
1 = = 250 = 50,92 см⁄с1 4,91
2 = = 250 = 50,92 см⁄с2 4,91
3 = = 250 = 316,46 см⁄с3 0,79
4 = = 250 = 50,92 см⁄с4 4,91
5 = = 250 = 50,92 см⁄с5 4,91
здесь – площадь живого сечения, при напорном движении жидкости площадь живого сечения равна площади поперечного сечения трубы, см2,
|
|
∙ 2 |
|
|
3,14 ∙ (2,5)2 |
|
|
1 = |
1 |
= |
|
|
= 4,91 см2 |
||
4 |
4 |
||||||
2 |
= |
∙ 22 |
|
= |
3,14 ∙ (2,5)2 |
|
= 4,91 см2 |
4 |
|
4 |
|
||||
3 |
= |
∙ 32 |
|
= |
3,14 ∙ (1,0)2 |
|
= 0,79 см2 |
4 |
|
4 |
|
||||
|
|
|
|
|
|
||
4 |
= |
∙ 42 |
= |
3,14 ∙ (2,5)2 |
|
= 4,91 см2 |
|
4 |
4 |
|
|||||
5 |
= |
∙ 52 |
|
= |
3,14 ∙ (2,5)2 |
|
= 4,91 см2 |
4 |
|
4 |
|
||||
|
|
|
|
|
|
||
d − внутренний диаметр трубы в см.
3)Далее вычисляются скоростные высоты, см, 2 для всех сечений. При
2
этом можно принять α=1,05, V – средняя скорость потока воды в данном живом сечении потока, см/с; g =982 см/с2 – ускорение свободного падения.
|
∙ 2 |
|
1,05 ∙ (50,92)2 |
|
|
1 |
1 |
= |
|
= 1,39 см |
|
2 |
2 ∙ 982 |
||||
|
|
||||
ПРИМЕР выполнения (06/04/2020) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Стр. 5 |
|
Лабораторная работа «Уравнение Даниила Бернулли» |
|
|
|
|
|||||||||||||||
|
|
|
2 |
∙ 2 |
|
|
|
1,05 ∙ |
(50,92)2 |
|
|
||||||||
|
|
|
|
|
|
2 |
|
|
= |
|
|
|
= 1,39 см |
||||||
|
|
|
|
|
2 |
|
|
|
|
|
2 ∙ 982 |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
3 |
∙ 2 |
|
|
1,05 ∙ (316,46)2 |
|
|
|||||||||||
|
|
|
|
3 |
|
|
= |
|
|
|
|
= 53,54 см |
|||||||
|
|
2 |
|
|
|
2 ∙ 982 |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
4 |
∙ 2 |
|
|
|
4,05 ∙ |
(50,92)2 |
|
|
||||||||
|
|
|
|
|
|
4 |
|
|
= |
|
|
|
= 1,39 см |
||||||
|
|
|
|
|
2 |
|
|
|
|
|
2 ∙ 982 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
5 |
∙ 2 |
|
|
|
4,05 ∙ |
(50,92)2 |
|
|
||||||||
|
|
|
|
|
|
5 |
|
|
= |
|
|
|
= 1,39 см |
||||||
|
|
|
|
|
2 |
|
|
|
|
|
2 ∙ 982 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
4) Вычисляется полная удельная потенциальная энергия (УПЭ) в данном |
|||||||||||||||||||
живом сечении, см : + |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
1 |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
+ |
|
= 25,00 + 70,00 = 95,00 см |
||||||||||||||
|
|
|
|
||||||||||||||||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
+ |
2 |
|
= 25,00 + 65,00 = 90,00 см |
|||||||||||||
|
|
|
|
||||||||||||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
+ |
3 |
= 25,00 + 5,00 = 30,00 см |
|||||||||||||
|
|
|
|
||||||||||||||||
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
+ |
4 |
|
= 25,00 + 55,00 = 80,00 см |
|||||||||||||
|
|
|
|
||||||||||||||||
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
+ |
5 |
|
= 25,00 + 45,00 = 70,00 см |
|||||||||||||
|
|
|
|
||||||||||||||||
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
5)Определяется напор (ПУЭ) в каждом сечении по формуле:
|
|
|
|
|
|
|
|
|
|
Н = z + |
p |
+ |
2 |
||
|
|
|
|
|
|
|
|
|
|
γ |
|
2 |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
p |
∙ 2 |
|
|
|
|
|
|
|
|||
Н |
= z |
+ |
1 |
+ |
1 |
|
= 25,00 + 70,00 + 1,39 = 96,39 см |
||||||||
|
|
|
|||||||||||||
|
1 |
1 |
|
|
γ |
2 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
p |
∙ 2 |
|
|
|
|
|
|
|
||
Н |
|
= z |
+ |
|
2 |
+ |
2 |
|
= 25,00 + 65,00 + 1,39 = 91,39 см |
||||||
2 |
|
|
|
||||||||||||
|
2 |
|
|
γ |
2 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
p |
∙ 3 |
|
|
|
|
|
|
|
||
Н |
|
= z |
+ |
|
3 |
+ |
3 |
|
= 25,00 + 5,00 + 53,54 = 83,54 см |
||||||
3 |
|
|
|
||||||||||||
|
3 |
|
|
γ |
3 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
p |
∙ 4 |
|
|
|
|
|
|
|
||
Н |
|
= z |
+ |
|
4 |
+ |
4 |
|
= 25,00 + 55,00 + 1,39 = 81,39 см |
||||||
4 |
|
|
|
||||||||||||
|
4 |
|
|
γ |
4 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
p |
∙ 5 |
|
|
|
|
|
|
|
||
Н |
|
= z |
+ |
|
5 |
+ |
5 |
|
= 25,00 + 45,00 + 1,39 = 71,39 см |
||||||
5 |
|
|
|
||||||||||||
|
5 |
|
|
γ |
5 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
||||
ПРИМЕР выполнения (06/04/2020) |
Стр. 6 |
Лабораторная работа «Уравнение Даниила Бернулли» |
|
6)Потеря напора на каждом рассматриваемом участке между соседними пьезометрами равна разности напоров в начале и в конце рассматриваемого участка:
1−2 = 1 − 2 = 96,39 − 94,39 = 5,00 см2−3 = 2 − 3 = 94,39 − 83,54 = 7,85 см3−4 = 3 − 4 = 83,54 − 84,39 = 2,45 см4−5 = 4 − 5 = 84,39 − 74,39 = 10,00 см
7)Пьезометрический уклон |
|
для |
каждого |
участка вычисляется по |
||||||||||||||||||||
|
∆УПЭ |
|
( + |
|
)−( |
|
|
|
+ |
+1 |
) |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
формуле: = |
= |
|
|
|
+1 |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
1−2 |
|
= |
95,00 − 90,00 |
= 0,4000 |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
50 |
|
|
|
|
|
|
|||||
|
|
|
|
2−3 |
|
= |
90,00 − 30,00 |
= 3,0000 |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
20 |
|
|
|
|
|
|
|||||
|
|
|
|
3−4 = |
30,00 − 80,00 |
= −2,5000 |
||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
20 |
|
|
|
|
|
|
|
||||
|
|
|
|
4−5 |
|
= |
80,00 − 70,00 |
= 4,0000 |
||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
400 |
|
|
|
|
|
|
|||||
8) Гидравлический |
|
уклон |
|
|
|
для |
каждого |
участка трубопровода |
||||||||||||||||
|
|
|
|
|
|
∆ПУЭ |
|
|
− |
|
|
|
|
|
||||||||||
вычисляется по формуле: = |
|
|
|
|
|
|
|
= |
|
+1 |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
4−2 = |
|
96,39 − 94,39 |
= 0,4000 |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
50 |
|
|
|
|||||||||||
|
|
|
2−3 = |
|
94,39 − 83,54 |
= 0,3923 |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
20 |
|
|
|
|||||||||||
|
|
|
3−4 = |
|
83,54 − 84,39 |
= 0,4077 |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
20 |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
84,39 − 74,394−5 = 400 = 4,0000
Все результаты измерений и вычислений заносятся в таблицу 1.
Таблица 1.
№ опыта
1
2
3
4
5
d
см
2,5
2,5
1,0
2,5
2,5
|
V |
|
см2 см/с
4,91 50,92
4,91 50,92
0,79 316,46
4,91 50,92
4,91 50,92
Z
см
25
25
25
25
25
p |
V |
|
2 |
|
2g |
|
см |
см |
70,00 |
|
1,39 |
|
65,00 |
1,39 |
5,00 |
53,54 |
55,00 |
1,39 |
45,00 |
1,39 |
|
|
+ |
|
|
H |
|
|||
|
|
|
|
см |
см |
95,00 |
|
96,39 |
|
90,00 |
91,39 |
30,00 |
83,54 |
80,00 |
81,39 |
70,00 |
71,39 |
|
|
№ участка
1-2
2-3
3-4
4-5
hw |
i |
I |
L |
|
|
|
|
см |
- |
- |
см |
5,00 |
|
|
|
0,1000 |
0,1000 |
50 |
|
7,85 |
0,3923 |
3,0000 |
20 |
2,15 |
0,1077 |
-2,5000 |
20 |
10,00 |
0,1000 |
0,1000 |
100 |
|
|
|
|

ПРИМЕР выполнения (06/04/2020) |
Стр. 7 |
Лабораторная работа «Уравнение Даниила Бернулли» |
|
Характер линий Р-Р и Н-Н при проведении лабораторной работы показан на рис.6.
Рис.6. Пьезометрическая и напорная линия в установке трубопровода переменного сечения
Заполнив таблицу 1, необходимо вычертить на листе миллиметровой бумаги формата А4 схему трубопровода и пьезометров, нанести на ней пьезометрические и скоростные высоты, построить напорную линию H-H (красным цветом) и пьезометрическую линию Р-Р (зелёным цветом) с указанием соответствующих значений в каждом сечении.
Нанести плоскость сравнения О-О, ось трубопровода и непосредственно сам трубопровод с указанием диаметров, обозначить живые сечения и длины участков.
Пример оформления трубопровода переменного сечения с нанесённой напорной линией Н-Н и пьезометрической линией Р-Р приведён на рис.7. Горизонтальный масштаб чертежа можно принять Мг1:20 (в 1 см – 20 см), вертикальный масштаб – Мв1:10 (в 1 см – 10 см).

ПРИМЕР выполнения (06/04/2020) |
Стр. 8 |
Лабораторная работа «Уравнение Даниила Бернулли» |
|
Рис. 7. Напорная и пьезометрическая линия для трубопровода переменного сечения
В заключение лабораторной работы следует проанализировать с помощью уравнения Д.Бернулли для каждого участка: а) изменение удельной кинетической энергии (увеличивается, уменьшается или остаётся постоянной), б) изменение удельной потенциальной энергии (увеличивается, уменьшается или остаётся постоянной), в) изменение полной удельной механической энергии (увеличивается, уменьшается или остаётся постоянной), а также г) знак гидравлического уклона (положительный или отрицательный) и д) знак пьезометрического уклона (положительный или отрицательный). Для этого необходимо заполнить таблицу 2. В выводах написать полный анализ уравнения Д.Бернулли.
Таблица 2. Анализ уравнения Даниила Бернулли
|
Удельная |
Удельная |
ПОЛНАЯ |
Пьезометрический |
Гидравлический |
|
участок |
кинетическая |
потенциальная |
удельная |
|||
уклон |
уклон |
|||||
|
энергия |
энергия |
энергия |
|||
|
|
|
||||
|
|
|
|
|
|
|
4-2 |
const |
↓ |
↓ |
+ |
+ |
|
|
|
|
|
|
|
|
2-3 |
↑ |
↓ |
↓ |
+ |
+ |
|
|
|
|
|
|
|
|
3-4 |
↓ |
↑ |
↓ |
— |
+ |
|
|
|
|
|
|
|
|
4-5 |
const |
↓ |
↓ |
+ |
+ |
|
|
|
|
|
|
|
ПРИМЕР выполнения (06/04/2020) |
Стр. 9 |
Лабораторная работа «Уравнение Даниила Бернулли» |
|
ВЫВОДЫ:
1)Ознакомились с энергетическим смыслом уравнения Д. Бернулли
2)Ознакомились с геометрическим смыслом уравнения Д. Бернулли и его графическим изображением
3)Провести анализ уравнения Д. Бернулли на примере трубопровода переменного сечения:
a)Удельная кинетическая энергия – может оставаться постоянной, уменьшаться или увеличиваться (при переходе потенциальной энергии в кинетическую)
b)Удельная потенциальная энергия – может уменьшаться или увеличиваться (при переходе кинетической энергии в потенциальную)
c)Полная удельная энергия - только уменьшается, так как в реальном мире движение жидкости всегда идёт с потерей энергии
d)Пьезометрический уклон – может быть положительным (когда потенциальная энергия уменьшается) и отрицательным (в случае, когда потенциальная энергия увеличивается)
e)Гидравлический уклон – всегда положительный, так как полная удельная энергия всегда уменьшается.
4)Построили напорную и пьезометрическую линии для трубопровода переменного сечения (на мм)
