
ФХ лр12
.pdf
Работа №12
Изучение скорости инверсии тростникового сахара.
Цель работы: определить углы вращения с помощью поляриметра, вычислить константы скорости для каждого момента реакции, рассчитать среднее значение kcр, подтвердить порядок реакции инверсии тростникового сахара.
Литература: Практикум 1986, с.319-324, 328-333, 339-340, 345-350 или Практикум 1974, с.322-346, 354-362
Теоретическая часть
Скорость химической реакции определяется изменением количества данного компонента в единицу времени в единице объема:
|
|
1 |
dn |
i 0 |
|
|
|||
i |
|
V d |
||
|
|
|||
где n-число молей данного компонента в объеме V данной фазы в момент времени t.
Если объем величина постоянная, то скорость определяется изменением концентрации реагирующего вещества за единицу времени:
V const : |
|
d n |
i |
/ V |
|
d c |
i |
|
|
|
|||||
i |
|
d |
|
d |
|||
|
|
|
|||||
Скорость реакции всегда положительна.
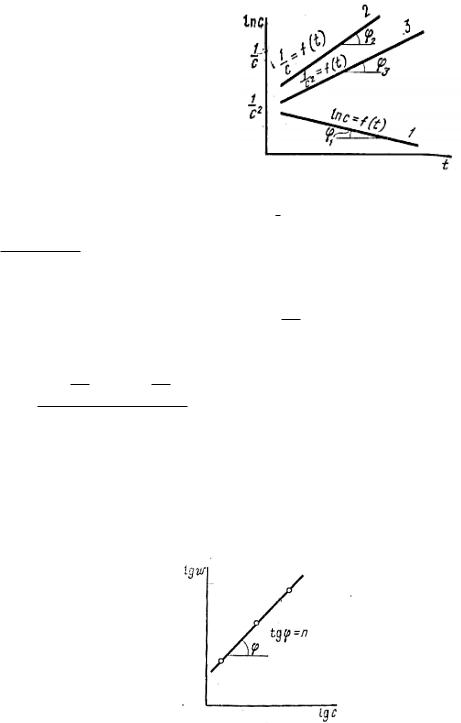
Кинетические кривые для исходных веществ(1) и продуктов реакции(2)
Основной постулат химической кинетики:
скорость реакции в каждый момент времени пропорциональна произведению возведенных в некоторую степень концентраций реагирующих веществ (закон действующих масс).
А А B B D D ... продукты,
|
d ci |
kcAp cBq cDr |
|
||
i d |
|
|
Коэффициент пропорциональности k называется константой скорости химической реакции. Ее физический смысл: константа скорости равняется скорости реакции при единичной концентрации, поэтому ее называют также

удельной скоростью реакции.
k (c |
1) |
i |
|
Величина константы зависит от всех факторов, которые влияют на скорость химической реакции, за исключением изменения концентрации реагирующих веществ. Числовое значение зависит так же от выбора единиц времени и концентрации. Размерность определяется тем кинетическим уравнением, по которому производится ее расчет, т.е. зависит от порядка реакции
Порядок реакции является эмпирической величиной. Частным называется порядок, характеризующийся изменением концентрации одного из веществ, вступающих в реакцию. Чтобы определить порядок по данному веществу, необходимо создать такие условия, чтобы в процессе реакции изменялась концентрация только данного вещества. Для этого концентрации всех остальных участников должны быть взяты в большом избытке. Сумма частных порядков дает общий порядок реакции.
Молекулярность реакции определяется числом частиц, участвующих в одном элементарном акте химического превращения.
Период полупревращения-это время, за которое исходная концентрация реагента уменьшится в 2 раза. Измерение периода полупревращения приносит большую пользу при исследованиях порядка реакции.
Математические выражения для расчета констант скорости реакций: 1. Необратимые реакции 1-го порядка
k1 ln c0
c
,
k, с |
1 |
|
2. Необратимые реакции 2-го порядка
|
1 |
|
1 |
|
1 |
|
|
1 |
|
|
x |
|
|||
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
с |
|
|
|
|
c0 |
c0 x |
|
|||||
|
|
|
с0 |
|
|
||||||||||
k, |
л |
|
с моль |
||
|
3. Необратимые реакции 3-го порядка
|
1 |
|
1 |
|
1 |
|
|
|
k |
|
|
|
|
|
|
|
, |
|
|
2 |
2 |
|||||
|
|
|
|
|
|
|
||
|
2 c |
|
|
c0 |
|
|
||
|
л |
2 |
|
|
|
k, |
|
|
|
||
моль |
2 |
с |
|||
|
|||||
|
|
||||
4. Необратимые реакции нулевого порядка
k |
c0 |
c |
, k, |
моль |
|
|
л с |
Где с0– начальная концентрация исходных веществ, с – концентрация после протекания реакции, t – время, х – концентрация прореагировавшего вещества за промежуток времени
Методы определения порядка реакции 1. Интегральные методы определения порядка реакции
а) метод подбора уравнения
1)аналитический – суть метода состоит в подстановке ci реагирующего
вещества для различных моментов времени от начала реакции в
кинетические уравнения различных порядков (1го, 2го , 3го и т.д ). Искомым является тот порядок, для которого наблюдается постоянство (неизменность) значения константы скорости реакции при различных концентрациях
2)графический – состоит в нахождении такой функции концентрации от времени, которая имела бы линейный характер:
1 порядок -
2 порядок -
3 порядок -
lnc 1/ c
1/ c
k const lnc
k const 1/ c0
2 2k const 1/
0 |
, |
|
, |
|
, |
c02 |
||
0 порядок -
с
k
c |
0 |
|
.
б) метод Оствальда-Нойеса – использует зависимость
|
lg |
/ |
|
|
|
n |
1/ 2 |
1/ 2 |
1 |
||
lg c |
|
/ c |
|
||
|
0,2 |
0,1 |
|
||
|
|
|
|
||
1
2
f
c |
0 |
|
:
3. Дифференциальные методы Вант-Гоффа
а) Аналитический метод – по двум значениям |
dc |
|
d |
||
|
1) по одной кинетической кривой – временной порядок
при двух
c
|
|
|
dc |
|
|
|
dc |
|
|
|
lg |
|
|
lg |
|
|
|||
n |
|
|
d |
1 |
|
|
|
d |
2 |
|
|
|
|
|
|
|
|
||
|
|
|
lg c |
lg c |
2 |
|
|
||
|
|
|
|
1 |
|
|
|
|
|
2) по 2ум начальным концентрациям – концентрационный порядок
|
|
|
dc |
|
|
dc |
||
|
lg |
|
|
|
lg |
|
|
|
|
|
|
||||||
n |
|
|
d 0,1 |
|
|
d 0,2 |
||
|
|
lg c0,1 |
lg c0,2 |
|||||
|
|
|
||||||
б) Графический вариант метода Вант-Гоффа
lg lg k n lg c
tg n .
.

Задача
Константа скорости реакции протолитического гидролиза сахарозы в 0.3 молярном растворе в присутствии 2.5 молей соляной кислоты равна 0.0133 мин-1 при температуре 20°С. Энергия активации данной реакции по справочным данным 106.94 кДж/моль. Приняв порядок реакции равным 1, рассчитать:
1.Константу скорости гидролиза при 30°С;
2.Период полупревращения реакции по сахарозе при той же температуре;
3.Время от начала реакции (в минутах), через которое при 30°С будет наблюдаться изменение знака угла вращения плоскости поляризации при поляриметрическом исследовании кинетики данной реакции. Чему
равна степень превращения сахарозы в этот момент времени? Граничные значения углов вращения плоскости поляризации реакционного
раствора в начальный момент времени и при полном завершении реакции при 30°С принять равными α0=19.6° и α∞= -7.1° соответственно.
1) Найдем константу скорости гидролиза при 30°С: По уравнению Аррениуса
( )
( )
мин-1 2) Определим период полупревращения реакции по сахарозе при 30°С:
Для реакции первого порядка период полупревращения равен –
Тогда, |
|
мин |
|
3)Найдем время от начала реакции (в минутах), через которое при 30°С будет наблюдаться изменение знака угла вращения плоскости поляризации при поляриметрическом исследовании кинетики данной реакции.
,
где - угол вращения в начальный момент времени, - угол вращения в данный момент времени, - угол вращения, соответствующий концу реакции.

мин Определим степень превращения сахарозы в этот момент времени:
, где β - степень превращения сахарозы
Ответ: |
мин-1 |
2. |
мин |
3. |
мин, |
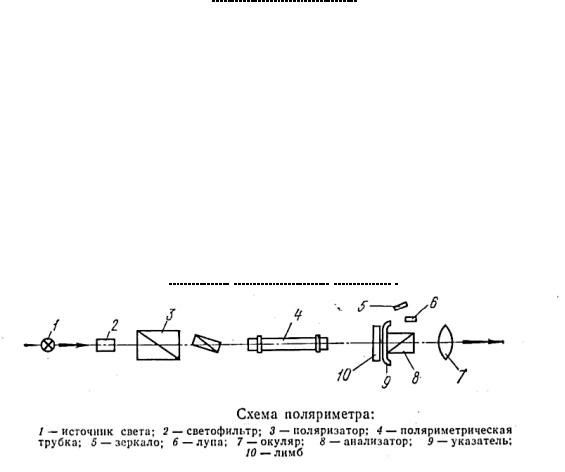
Экспериментальная часть
Задание на работу Исследовать процесс инверсии сахара:
С12Н22О11 + Н2О ―› С6Н12О6 + С6Н12О6
глюкоза фруктоза
Условия проведения эксперимента:
20% -ный раствор тростникового сахара
Катализатор – 3н. HCl
Для определения угола вращения соответствующий концу реакции
Катализатор - 6н. HCl
Температура - 40˚С
Порядок выполнения работы
1.Приготовить 50мл 20% -ного раствора тростникового сахара.
2.Отобрать в колбу 25 мл этого раствора, влить 25 мл 6н. HCl. Смесь перемещать и поместить в термостат при 40˚С на 3-3,5 часа.
3.Оставшиеся 25 мл раствора сахара смешать с 25мл раствора 3н.HCl (момент сливания отметить как момент начала реакции).
4.Смесь перемешать и влить в чистую поляриметрическую трубку, которую помещаем в желобок поляриметра.
5.Выполнить 10-12 определений.
6.Определить угол вращения α соответствующий концу реакции
измеряем по первому приготовленному раствору
7.Вычислить константы скорости для каждого момента рассчитать kср и сравнить полученное значение с kср , найденной на графике ln(αt – α∞) = f(t) .

Обработка экспериментальных данных
№ |
, |
|
|
|
|
мин |
|
|
|
мин –1 |
|
|
|
|
|
|
|
1 |
4 |
19,20 |
26,85 |
3,29 |
0,0266 |
|
|
|
|
|
|
2 |
8 |
17,65 |
25,3 |
3,23 |
0,0208 |
|
|
|
|
|
|
3 |
10 |
16,20 |
23,85 |
3,17 |
0,0225 |
|
|
|
|
|
|
4 |
12 |
15,15 |
22,8 |
3,13 |
0,0225 |
|
|
|
|
|
|
5 |
14 |
14,20 |
21,85 |
3,08 |
0,0223 |
|
|
|
|
|
|
6 |
17 |
13,10 |
20,75 |
3,03 |
0,0214 |
|
|
|
|
|
|
7 |
20 |
11,50 |
19,15 |
2,95 |
0,0222 |
|
|
|
|
|
|
8 |
23 |
9,75 |
17,4 |
2,86 |
0,0235 |
|
|
|
|
|
|
9 |
26 |
9,50 |
17,15 |
2,84 |
0,0213 |
|
|
|
|
|
|
10 |
29 |
8,10 |
15,75 |
2,76 |
0,0221 |
|
|
|
|
|
|
11 |
34 |
6,30 |
13,95 |
2,64 |
0,0224 |
|
|
|
|
|
|
12 |
39 |
4,70 |
12,35 |
2,51 |
0,0226 |
|
|
|
|
|
|
∞ |
∞ |
-7,65 |
- |
- |
- |
|
|
|
|
|
|
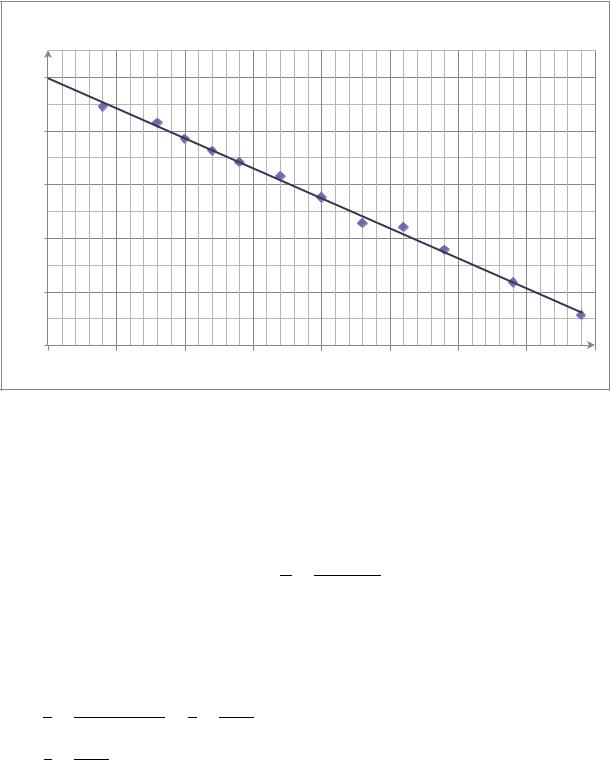
Построим график зависимости ln(αt – α∞) = f(t).
Для этого рассчитаем значения ln(αt – α∞), где α∞= - 7,65˚
1) |
( |
— |
) |
2) |
( |
— |
) |
3) |
( |
— |
) |
4) |
( |
— |
) |
5) |
( |
— |
) |
6) |
( |
— |
) |
7) |
( |
— |
) |
8) |
( |
— |
) |
|
|
|
|
|
|
9) |
( |
— |
) |
|
|
|
|
|
|
10) |
( |
— |
) |
|
|
|
|
|
|
11) |
( |
— |
) |
|
|
|
|
|
|
12) |
( |
— |
) |
|
51 |
|
|
|
|
|
|
График зависимости ln(αt – α∞) = f(t) |
|
||||||
3,4 |
|
ln(αt – α∞) |
|
|
|
|
|
y = -0,0223x + 3,397 |
|
|
|
|
|
|
|
|
|
|
|
3,2 |
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
2,8 |
|
|
|
|
|
|
|
|
|
2,6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
2,4 |
|
|
|
|
|
|
|
|
мин |
|
|
|
|
|
|
|
|
|
|
|
0 |
5 |
10 |
15 |
20 |
25 |
30 |
35 |
40 |
Константа скорости по графику: |
|
|
|
|
|
||||
ср |
мин-1 |
Из графика методом экстраполяции определили: ln(α0 – α∞)=3,397 Откуда α0 =
Вычислим константу скорости реакции при данной температуре :
где - угол вращения в начальный момент времени, - угол вращения в данный момент времени, - угол вращения, соответствующий концу реакции, t – время, протекшее от начала реакции до момента данного измерения
мин-1
мин-1

мин-1
мин-1
0,0223 мин-1
0,0214 мин-1
0,0222 мин-1
0,0235 мин-1
0,0213 мин-1
0,0221 мин-1
0,0224 мин-1
0,0226 мин-1
∑
ср
мин-1
Вывод:
В ходе данной лабораторной работы мы изучили кинетику реакции инверсии тростникового сахара по измерению угла вращения плоскости поляризации.
С12Н22О11 + Н2О ―› С6Н12О6 + С6Н12О6
глюкоза фруктоза
Определили углы вращения:
в начальный момент времени α0
соответствующий концу реакции α∞ = - 7,65˚
Подтвержден 1-ый порядок реакции. Для этого был использован интегральный метод определения порядка реакции:
1)аналитический -
2)графический -
ср мин-1
ср мин -1
Расхождение полученных констант несущественно.
