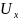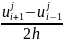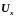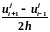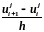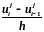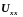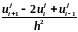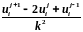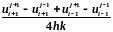Матмод. Вопросы к экзамену
.docx
Вопросы к экзамену «по математическому моделированию»
Лекция 1
1.1 Определение скалярного поля.
Скалярным полем называется пространство, в каждой точке Р которого определена скалярная функция U =U(P)
1.2 Перечислите характеристики скалярного поля.
Линии уровня, градиент функции и производная по направлению вектора.
1.3 Определение линии уровня.
Функции уравнения U(M)=C
1.4 Определение поверхностей уровня.
Поверхностью уровня скалярного поля u=u(x,y,z) называется множество точек пространства, в которых функция u принимает одно и то же значение C, то есть поверхность уровня определяется уравнением u(x,y,z)=C
1.5 Определение градиента функции.
Вектор, своим направлением указывающий направление наискорейшего возрастания некоторой величины, значение которой меняется от одной точки пространства к другой, а по величине равный быстроте роста этой величины в этом направлении.
1.6 Свойство градиента функции, проведенного к линии (поверхности) уровня.
Основное свойство градиента в данной точке перпендикулярна линии проходящей через эту точку.
1.7 Что задаёт градиент функции.
Градиент задаёт направление наибольшего роста функции в данной точке.
1.8 Что характеризует длина градиента вектора.
Длина градиента вектора характеризует наибольшую скорость изменения поля в данной точке.
1.9 Определение производной функции по направлению вектора.
это обобщение понятия производной на случай функции нескольких переменных. Производная по направлению показывает, насколько быстро функция изменяется при движении вдоль заданного направления.
1.10 Физический смысл производной по направлению.
Скорость изменения функции по при движении в данном направлении
1.11 Чему равна производная по направлению перпендикулярному градиенту функции.
Производная по направлению перпендикулярному градиенту функции равна 0.
1.12 Когда производная по направлению принимает наибольшее значение.
Производная поля по направлению принимает наибольшее значение, когда выбранное направление совпадает с направлением градиента, в этом случае производная принимает своё наибольшее значение, модуль градиента.
1.13 Определение векторного поля.
Если
в некоторой области пространства каждой
точке M по
определённому закону ставится в
соответствие вектор ![]() ,
то векторная функция
,
то векторная функция ![]() называется
полем вектора или векторным полем.
называется
полем вектора или векторным полем.
Таким образом, векторным полем является векторная функция точки пространства
![]()
1.14 Как задаётся векторное поле.
Векторное поле задаётся векторной функцией точки:
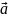 =
(M)=
(x,y,z)=P(x,y,z)
=
(M)=
(x,y,z)=P(x,y,z)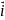 +Q(x,y,z)
+Q(x,y,z)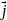 +R(x,y,z)
+R(x,y,z)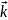 =(P,Q,R);
=(P,Q,R);
1.15 Перечислите характеристики векторного поля.
Ротор; вихрь; дивергенция; линии тока.
1.16 Как задаются линии тока.
Линии тока- это силовые или векторные линии поля, которые задаются системой ДУ(дифференциальных уравнений):
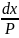 =
=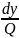 =
=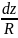 ;
;
1.17 Дать определение ротора.
Ротор(вихрь)- определяет меру и направление завихрённости силовых линий.
rot
=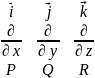
1.18 Сформулировать условие потенциальности поля в односвязной области.
Поле называется потенциальным в односвязной области, если rot =0.
1.19 Физическая трактовка вихря.
υ = ω × r ,
где ω – мгновенная угловая скорость; r – радиус-вектор, проведенный из центра вращения в произвольную точку тела.
Координаты вектора υ равны
![]()
Вычислим rot υ :
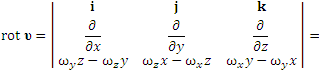
![]()
Таким образом, ротор вектора скорости υ характеризует "вращательную компоненту" поля скорости: .
![]()
1.20 Дать определение дивергенции.
Дивергенция(расходимость)-определяет наличие источников истоков в области G,где мы рассматриваем наше поле.
div
= +
+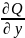 +
+ ;
;
1.21 Что определяет дивергенция.
Определяет наличие источников истоков в области G,где мы рассматриваем наше поле.
1.22 Какое поле называется соленоидальным: Если векторное поле не имеет источников или истоков, то оно называется соленоидальным.
1.23 Сформулировать условие соленоидальности поля:
Дивергенция
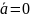
Лекция 2
2.1 Определение потока векторного поля через заданную поверхность:
Поток векторного поля, через поверхность σ, с единичной нормалью n вычисляется , как поверхностный интеграл второго рода.
П=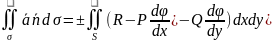
Z=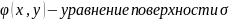
S-проекция
поверхности
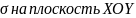
2.2 Как задается знак в формуле потока векторного поля
Знак
выбирается в зависимости от угла между
нормалью
 и z
, если он острый , то «+», если тупой «-»
и z
, если он острый , то «+», если тупой «-»
2.3
Для какой
поверхности при вычислении потока
векторного поля справедлива теорема
Гаусса –Остроградского:
Для замкнутой поверхности
2.4 Выписать формулу Гаусса –Остроградского
П=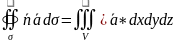
2.5 В чём состоит суть теоремы Гаусса –Остроградского
выражает поток
векторного поля через
замкнутую поверхность интегралом от дивергенции этого
поля по объёму,
ограниченному этой поверхность о
есть интеграл
от дивергенции векторного поля ![]() ,
распространённый по некоторому объёму
,
распространённый по некоторому объёму ![]() ,
равен потоку вектора
через поверхность
,
равен потоку вектора
через поверхность ![]() ,
ограничивающую данный объём.
,
ограничивающую данный объём.
2.6 Определение циркуляции векторного поля
Циркуляция
векторного поля по замкнутому
,ориентированному контуру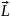 ,
определяется, как криволинейный интеграл
второго рода
,
определяется, как криволинейный интеграл
второго рода
Г=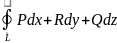
2.7
Результат
вычисления криволинейного интеграла
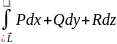 в
случае незамкнутого контура
.
в
случае незамкнутого контура
.
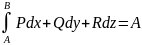 (равен
работе, по перемещению из точки А в точку
В).
(равен
работе, по перемещению из точки А в точку
В).
2.8 Для каких контуров при вычислении циркуляции поля справедлива теорема Стокса.
Для
замкнутого контура
Д


2.9 Сформулировать теорему Стокса
Г=
2.10 10 В чем суть теоремы Стокса
Смысл этой теоремы состоит в том, что циркуляция вектора a по произвольному контуру Г равна потоку вектора rot a через произвольную поверхность S, ограниченную данным контуром.
2.11 Что означает согласование направлений нормали и обхода контура.
Если из конца нормали обход контура L виден против часовой стрелки, то в формуле Г=
Берем «+», в противном случае «-».
2.12 Какое поле называется потенциальным
Если
поле имеет потенциал W,
то есть
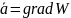 ,
то оно называется потенциальным.
,
то оно называется потенциальным.
2.13 Выписать выражение потенциала в случае потенциального поля.
A=W(A)-W(B)
W=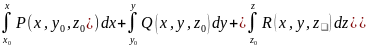
x,y,z-текущая точка
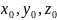 -любая
фиксированная точка выбираем сами
-любая
фиксированная точка выбираем сами
Лекция 3
3.1 Как формулируется задача Коши для обыкновенного ДУ I порядка
ДУ
I
– общ.вид:

Общее
решение:
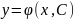 – совокупность интегральных кривых
– совокупность интегральных кривых
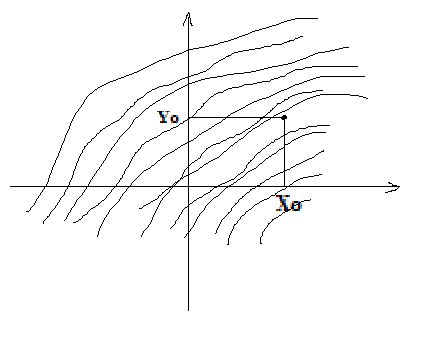
3.2 Отличие формулировок задачи Коши для обыкновенного ДУ I порядка, решаемой аналитическими и численными методами
Аналитическими:
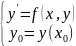
Численными:
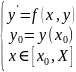
3.3 Дать определение сетки на отрезке
Сеткой
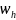 на отрезке
на отрезке
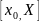 называется
упорядоченное множество точек, такое,
что
называется
упорядоченное множество точек, такое,
что
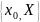 – граничные точки (входят в сетку);
– граничные точки (входят в сетку);
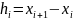 – шаг сетки.
– шаг сетки.
3.4 Какая сетка называется равномерной?
Если
шаг сетки
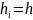 равен постоянной величине и вычисляется
как
равен постоянной величине и вычисляется
как
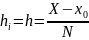 ,
сетка называется равномерной и все узлы
вычисляются по формуле
,
сетка называется равномерной и все узлы
вычисляются по формуле
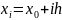
3.5 Какие функции называются сеточными
Функции, вычисленные в узлах сетки, называются сеточными функциями
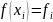
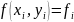
3.6 Какие выражения называются разностными производными?
Ра́зностное уравне́ние — уравнение, связывающее значение некоторой неизвестной функции в любой точке с ее значением в одной или нескольких точках, отстоящих от данной на определенный интервал
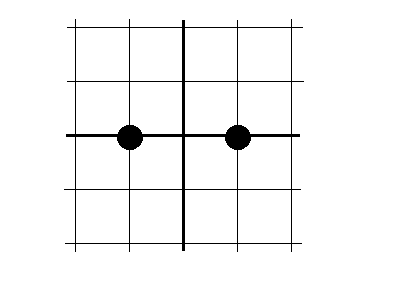
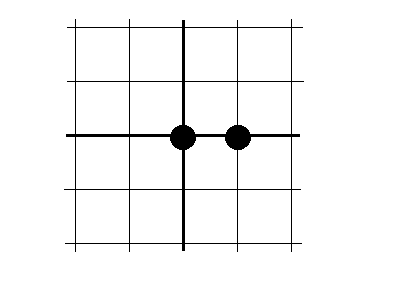
Разностными производными называют выражения следующего вида:
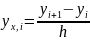 - правая
разностная производная О(h)
- правая
разностная производная О(h)
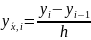 - левая
разностная производная О(h)
- левая
разностная производная О(h)
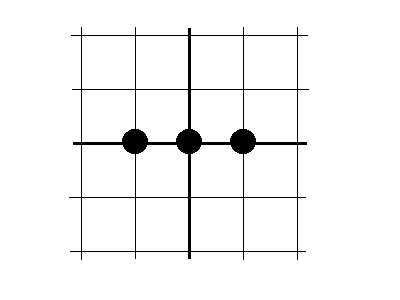
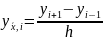 - центральная
разностная производная О(
- центральная
разностная производная О(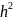 )
)
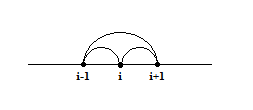
Погрешность центральной разностной производной меньше, чем у левой и правой О( )< О(h)
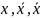 – обозначение для
различения формул
– обозначение для
различения формул
О(h) – порядок (оц.погрешности)
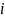 – узел сетки
– узел сетки
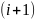 – узел сетки
– узел сетки
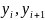 - сеточные функции
- сеточные функции
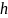 - равномерная сетка
- равномерная сетка
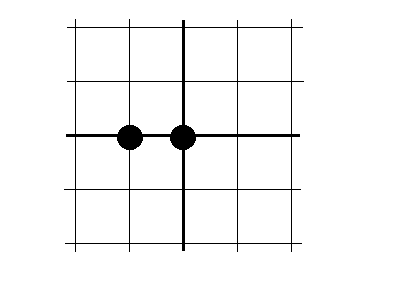
3.7 Привести расчетную формулу левой разностной производной
- левая разностная производная О(h)
3.8 Привести расчетную формулу правой разностной производной
- правая разностная производная О(h)
3.9 Привести расчетную формулу центральной разностной производной
- центральная разностная производная О( )
3.10 Какой процесс называется дискретизацией задачи.
Это процесс преобразования непрерывной функции в дискретную.
3.11 . Записать дискретный аналог произвольного дифференциального уравнения I порядка.
|
|
3.12 . Определение разностной схемы.
Семейство уравнений, зависящее от параметра h, называется разностной схемой.
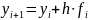
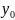 задано
задано
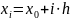
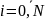
3.13 Определение разностной задачи.
Разностная схема при конкретном значении h называется разностной задачей
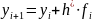
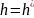
задано
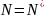
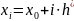
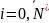
3.14 Для каких функций задача сводится к решению дифференциального уравнения в частных производных.
Для функций многих переменных f(x, y)
3.15 Общий вид линейного дифференциального уравнения II порядка для функций с двумя независимыми переменными.
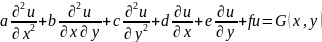
3.16 Общий вид однородного линейного дифференциального уравнения II порядка для функций с двумя независимыми переменными.
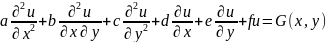
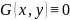 *
*
3.17 Что означают начальные условия в задачах математической физики.
Начальные условия представляют собой картину изучаемого процесса в фиксированный момент времени.
3.18 Что означают граничные условия в задачах математической физики.
Граничные условия представляют собой описание режима протекания процесса на границе области
3.19 Записать граничные условия I порядка
t = f1(x,y,z,τ)
t = const
Граничные условия 1-го рода определяют температуры на границах реактора для любого
момента времени:
T (t, x 0) 1(t),
T (t, x l) 2 (t).
3.20 Записать граничные условия II порядка
q =
Граничные условия 2-го рода задают изменение температуры на границах реактора для любого момента времени:
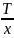 (t,
x 0)
= 1(t)
(t,
x 0)
= 1(t)
(t, x l) 2 (t)
3.21 Описать дискретзацию области решения краевой задачи
Определение.
Пусть
в области
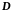 с непрерывной границей Г
в декартовой системе координат
с непрерывной границей Г
в декартовой системе координат
 поставлена краевая задача, то есть
ищется решение дифференциального
уравнения
поставлена краевая задача, то есть
ищется решение дифференциального
уравнения
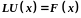 ,
,
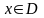 , (1)
, (1)
с краевыми (граничными, начальными) условиями
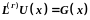 ,
,
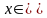 Г, (2)
Г, (2)
где
 и
и
 –
линейные дифференциальные операторы;
–
линейные дифференциальные операторы;
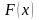 и
и
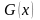 – заданные функции.
– заданные функции.
Введем прямоугольную
сетку
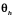 с узлами
с узлами
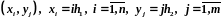
и сеточные функции
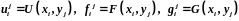 .
.
Область
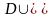 Г
приближенно заменим дискретным множеством
точек – сеточной областью
Г
приближенно заменим дискретным множеством
точек – сеточной областью
 ,
а производные, входящие в (1)–(2), –
разностными отношениями. В результате
получим систему линейных алгебраических
уравнений:
,
а производные, входящие в (1)–(2), –
разностными отношениями. В результате
получим систему линейных алгебраических
уравнений:
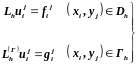 , (3)
, (3)
где
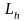 и
и
 – разностные операторы.
– разностные операторы.
Семейство уравнений
(3), зависящее от параметра
 ,
называется разностной
схемой.
,
называется разностной
схемой.
Разностную схему при конкретном значении будем называть разностной задачей
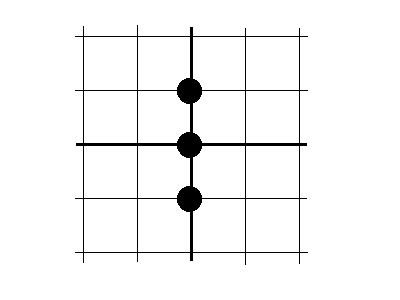
3.22 Привести шаблоны для разностных аналогов частных производных первого порядка
Производная |
Разностный аналог производной |
Шаблон |
|
|
|
|
|
|
|
|
|
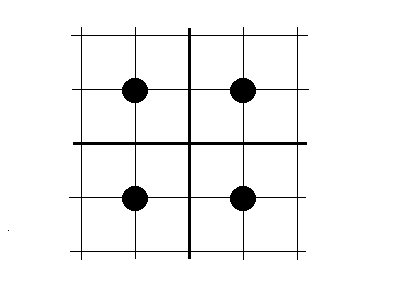
3.23 Привести шаблоны для разностных аналогов частнх производных второгоо порядка
Производная |
Разностный аналог производной |
Шаблон |
|
|
|
|
|
|
|
|
|
3.24
3.25
3.26 Дать определение слоя
Совокупность узлов I и j , одна из переменных имеет постоянные значение
3.27
3.28 Записать разностное уравнение для уравнения Пуассона в краевой задаче
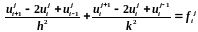 ,
,
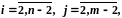
3.29 Записать разностную схему краевой задачи для уравнения Пуассона
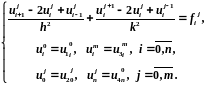
Лекция 4
4.1 Цель решения современных инженерных задач.
точное решение таких задач играет большую роль в формировании правильного понимания качественных особенностей многих явлений и процессов
К современным инженерным задачам относятся, например:
Создание новой конструкции.
Разработка нового технологического процесса или новой технологии (компьютера).
Разработка оптимального процесса.
4.2 На основании чего принимается решение в современных инженерных задачах.
В основе этих задач лежит процесс принятия решения. Решение принимается на основе данных, экспериментальных или вычислительных.
4.3 Особенности современных инженерных задач.
Инженерные задачи имеют выраженную практическую направленность, из чего следует доведение результатов до конкретных графиков, чисел, таблиц и т.д.
Большой объём вычислительной работы, сопровождающей решения и необходимость использовать современные вычислительные средства.
Для этих задач характерно использование достаточно сложных математических моделей и серьёзного математического аппарата.
Наличие и относительная доступность массового пользователя современного программного обеспечения.
4.4 Каким наиболее часто используемым методом решаются современные инженерные задачи.
Основной метод решения современных инженерных задач - это вычислительный эксперимент.
4.5 Основные этапы вычислительного эксперимента.
Инженерная постановка задачи.
↓
Математическая модель задачи (ключевой этап решения задачи).
↓
Дискретная модель.
↓
Выбор численного метода и его реализации.
↓
Обработка результатов.
4.6 Дать определение математической модели.
Математическая модель – приближённое описание внешнего мира, выраженного с помощью математических символов.
4.7 Дать определение математического моделирования.
Процесс построения и изучения математических моделей называется математическим моделированием.
4.8 Сформулировать этапы процесса математического моделирования.
Процесс математического моделирования можно, условно, разделить на 4 этапа:
Формулирование законов, связывающих основные объекты модели на языке той или иной науки. Запись в математических терминах, сформулированных качественных представлений о связях между объектами моделей.
Исследования математической задачи, к которой приводится математическая модель (метод решения, алгоритм, программа, расчёт).
Анализ результатов (Выяснение того, удовлетворяет ли принятая гипотетическая модель критерию практики; согласуются ли результаты наблюдений с теоретическими средствами моделей в пределах точности наблюдений).
Последующий анализ модели, в связи с накоплением данных об изучаемом объекте. Модернизация модели.
4.9 Дать определение вычислительной модели.
Вычислительная модель - типовая абстрактная или конкретная задача, соответствующая проблеме численного решения некоторого класса математических или прикладных задач.
4.10
4.11 Описать структуру вычислительной погрешности.
Пусть а – точное значение некоторой величины (неизвестное).
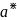 - приближённое
значение искомой величины (известное).
- приближённое
значение искомой величины (известное).
4.12 Что называется ошибкой (или погрешностью) приближённого числа.
Ошибкой (погрешностью) приближённого числа называется разность между точным и приближённым значениями. а- .
4.13 Количественные меры ошибки.
Количественными мерами ошибки являются абсолютная и относительная погрешности.
4.14 . Определение Абсолютной погрешности.
Если а
- точное значение некоторой величины,
а а* -
известное приближение к нему, то
абсолютной погрешностью
приближения а* называют
обычно некоторую величину ![]() ,
про которую известно, что она удовлетворяет
неравенству:
,
про которую известно, что она удовлетворяет
неравенству:
![]()
4.15 Определение Относительной погрешности.
Относительной
погрешностью называют некоторую
величину ![]() ,
про которую известно, что она удовлетворяет
неравенству:
,
про которую известно, что она удовлетворяет
неравенству:
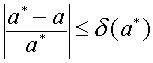
Относительную погрешность часто выражают в процентах. Она дает более точное представление о величине ошибки, содержащейся в некоторой величине.
4.16
4.17
4.18
4.19 Какую задачу называют хорошо обусловленной.
Под обусловленностью вычислительной задачи понимают чувствительность ее решения к малым изменениям входных данных. Задачу называют хорошо обусловленной, если при малых изменениях входных данных отвечают малые погрешности решения и результат также изменяется незначительно.
4.20 . Какую задачу называют плохо обусловленной.
Задача называется плохо обусловленной, если малые изменения входных данных могут привести к большим изменениям решения.