
Контрольная работа 2 Никитина Дарья ПИН 31Д
.docx
Контрольная работа 2
Интерактивные графические системы
Никитина дарья пин-31д

Кривая представляется в параметрическом виде следующей системой уравнений:

В рамках формы Эрмита предполагаем, что для начальной точки t=0, а для конечной t=1.
Касательный вектор в точке для координаты х выглядит следующим образом:
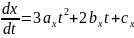
Перепишем формулы для функции x(t) и касательного вектора для координаты х в матричном виде:

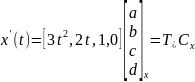
Задача
построения кривой сводится к нахождению
значений элементов матрицы
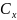 .
.
Подставим значения t=0 и t=1:

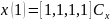
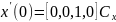
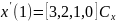
Объединив полученные выражения в одно матричное уравнение, получим:
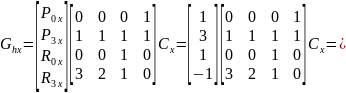
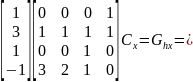
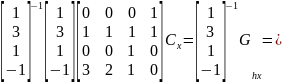


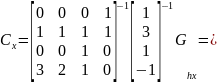
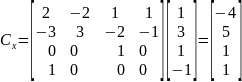
Это значит, что искомое уравнение из первой системы для координаты х выглядит следующим образом:
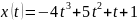
Аналогичным образом вычислим уравнение для переменной у.
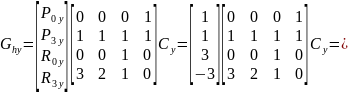
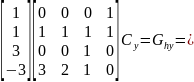
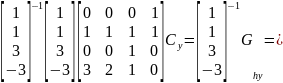
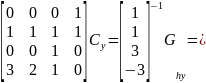
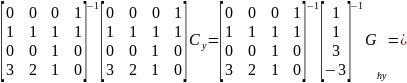
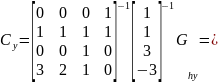
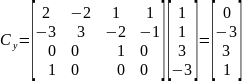
Значит, что искомое уравнение из первой системы для координаты у выглядит следующим образом:
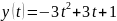
Итоговая система, представляющая кривую, выглядит так:

Касательный вектор в точке будет представлен следующей системой уравнений:
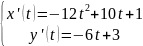
Вычислим значения в точках:
t=0
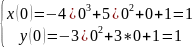
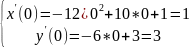
t=1/3
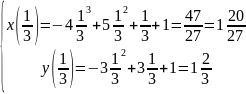
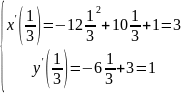
t=1/2
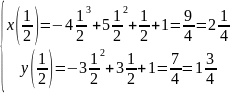
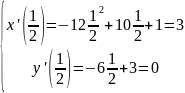
t=2/3
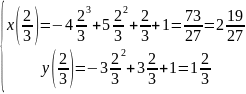
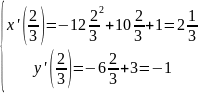
t=1

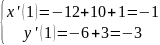
Графическое изображение кривой будет выглядеть следующим образом:
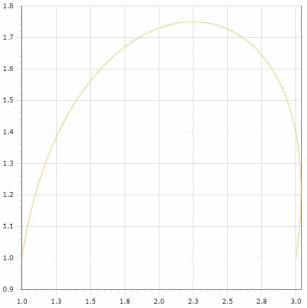
Если
значение вектора
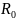 изменить на значение [2,6], то расчёты
изменятся следующим образом.
изменить на значение [2,6], то расчёты
изменятся следующим образом.


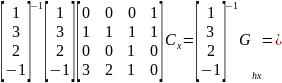
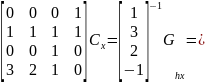

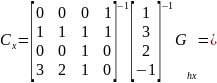
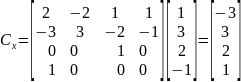
Это значит, что искомое уравнение из первой системы для координаты х выглядит следующим образом:
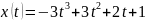
Аналогичным образом вычислим уравнение для переменной у.
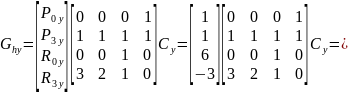

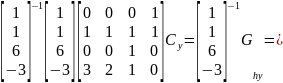
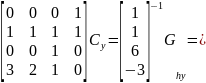
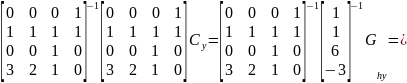
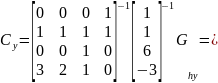
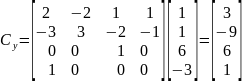
Значит, что искомое уравнение из первой системы для координаты у выглядит следующим образом:

Итоговая система, представляющая кривую, выглядит так:
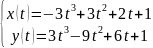
Касательный вектор в точке будет представлен следующей системой уравнений:

Вычислим значения в точках:
t=0

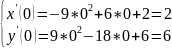
t=1/3
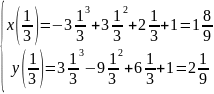

t=1/2
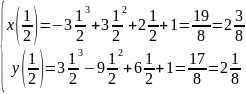

t=2/3
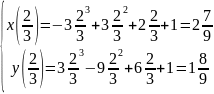
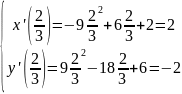
t=1
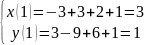

Графическое изображение кривой будет выглядеть следующим образом:
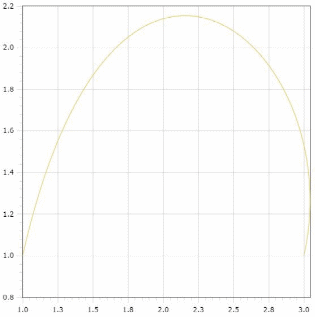
Относительно первого варианта график растянулся вдоль оси у.
