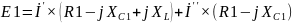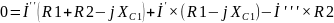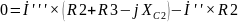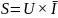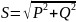Контрольная работа №2

1 Задание и исходные данные.

Заданием на контрольную работу является:

- расчёт цепи переменного тока в символическом виде методом контурных токов;

- расчёт цепи переменного тока в символическом виде методом узловых потенциалов;

- полный расчёт цепи переменного тока одним из вышеуказанных методов;

- для полного расчёта выполнить проверку по балансу мощности.

Исходные данные элементов цепи сведены в таблицу 1.

Таблица 1 - Исходные данные элементов цепи

R1, Ом	R2, Ом	R3, Ом	C1, мкФ	C2, мкФ	L, мГн	f, Гц	Е1, В
32	40	20	200	300	70	50	25

Схема цепи изображена на рисунке 1.

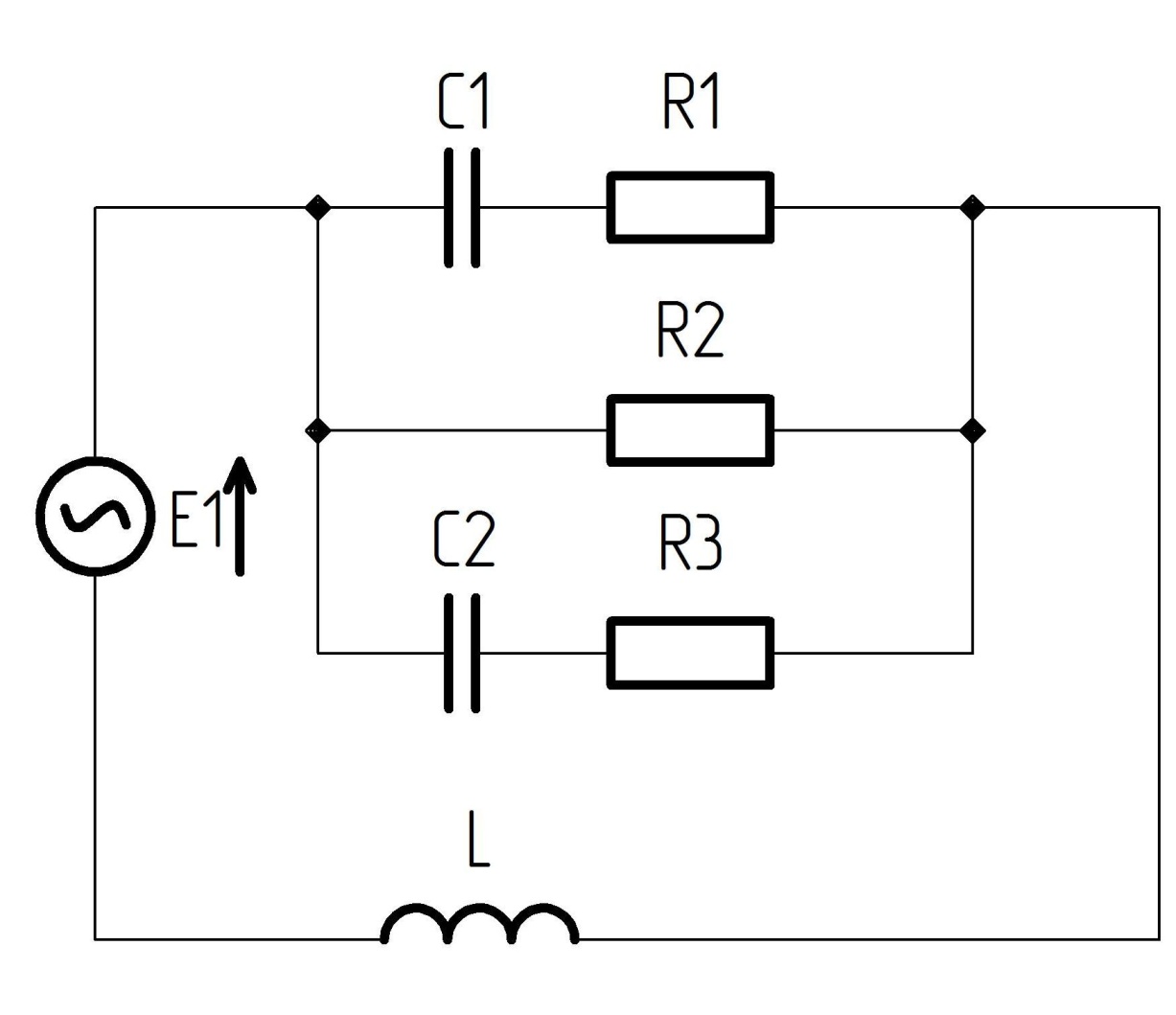
Рисунок 1 - Схема цепи переменного тока

Для большей наглядности преобразуем исходную схему, расставим направления токов в ветвях и пронумеруем узлы.

Рисунок 2 - Преобразованная схема цепи.

2 Расчёт цепи методом контурных токов.

Расчёт цепи методом контурных токов позволяет ограничиться лишь решением системы уравнений по второму закону Кирхгофа [1, с.31]. Для расчёта цепи данным методом требуется:

- выбрать произвольные направления токов во всех ветвях цепи;

- выбрать независимые контура и задать направления контурных токов;

- составить уравнения по второму закону Кирхгофа для контурных токов в том же количестве, что и для метода расчёта цепей по законам Кирхгофа.

Направления обхода контуров совпадают с направлениями контурных токов (Рисунок 3). Составляем уравнения по второму закону Кирхгофа для цепи переменного тока.

На основе полученных уравнений составим матрицы А и В для дальнейшего решения в программе MathCAD:

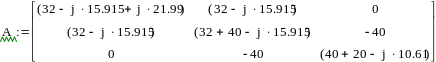
Путём умножения обратной матрицы А^-1 на матрицу В получим матрицу K c искомыми контурными токами:

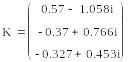
Таким образом I'=0,57-j1,058 A, I''= –0,37+j0,766 A, I'''=-0.327+j0,453 A.

Найдём токи в ветвях, с учётом того, что токи в ветвях дерева определяются как алгебраическая сумма контурных токов в ветви, а в ветвях связи токи по модулю равны токами контурным, и значение их зависит от совпадения направлений (при совпадении ток имеет положительное значение, если нет - отрицательное). [1, с.36-37]

I₁=I'+I''=0,199–j0,292 А

I₂=I'''–I''=0,043–j0,313 А

I₃=I'''= –0,327+j0,453 А

I₄=I'=0,57–j1,058 А

Проверка по балансу мощности произведена в программе MathCAD согласно формулам:

(2.1)[1, c.60]

(2.2)[1, c.60]

Погрешность расчётов δ=0%.

По полученным результатам составим векторную диаграмму токов в ветвях.

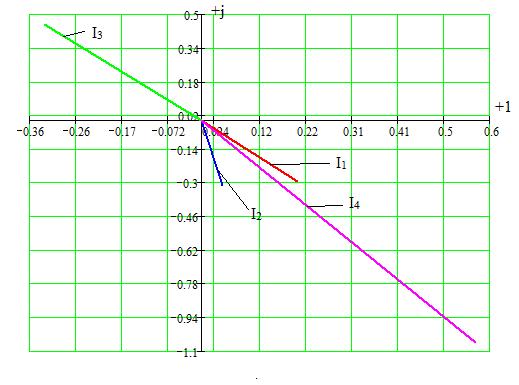
Рисунок 3 – Векторная диаграмма токов.

4 Расчёт цепи методом узловых потенциалов

Метод узловых потенциалов основан на том, что ток равен результату деления напряжения на сопротивление. В данном методе падение напряжения на пассивных элементах цепи представляется как разница потенциалов. [2, c.11, 21–22]

Направления токов расставлены согласно рисунку 1, узел №2 ­– заземлён.

Составим уравнения по первому закону Кирхгофа для узлов, которые не заземлены.

İ₄–İ₁–İ₂–İ₃=0

Представим токи в виде частного от деления разницы потенциалов и сопротивления:

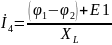
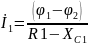
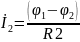
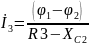
Литература

1 Покотило, С.А. Справочник по электротехнике и электронике/ Покотило С.А. - Ростов н/Д: Феникс. - 2012. - 282с., ил.

2 Коновалов, Б.И. Теоретические основы электротехники: Учебное пособие / Коновалов Б.И. - Томск: Томский межвузовский центр дистанционного образования. - 2006. - Ч.1 - 145с.