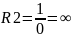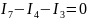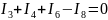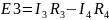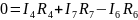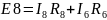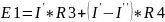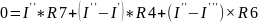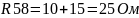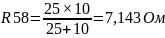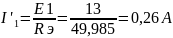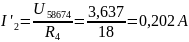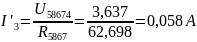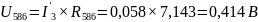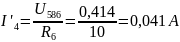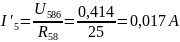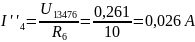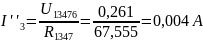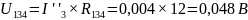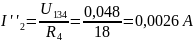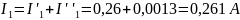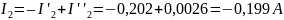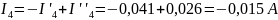Контрольная работа №1

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ

Федеральное государственное бюджетное образовательное учреждение высшего образования

Томский государственный университет систем управления и радиоэлектроники (ТУСУР)

Кафедра промышленной электроники

КОНТРОЛЬНАЯ РАБОТА №1

по дисциплине "Теоретические основы электротехники"

на тему: "Расчёт цепей постоянного тока"

Выполнил: студент гр. з-66 __________ О. Д. Чиркин Проверил: преподаватель __________ В.Н.Башкиров “__” ________ 2018г.

2018 г.

1 Задание и исходные данные.

Заданием на контрольную работу является расчёт цепи постоянного тока следующими методами:

- методом законов Кирхгофа;

- методом контурных токов;

- методом узловых потенциалов;

- методом наложения;

- методом эквивалентного генератора.

Для всех методов необходимо выполнить проверку по балансу мощности.

Исходные данные элементов цепи сведены в таблицу 1.

Таблица 1 - Исходные данные элементов цепи

R1, Ом	g2, См	R3, Ом	R4, Ом	R5, Ом	R6, Ом	g7, См	R8, Ом	Е1, В	Е3, В	Е4, В	Е5, В	Е6, В	Е8, В
18	0	30	22	16	14	0,04	24	0	4	0	14	0	20

Схема цепи изображена на рисунке 1.

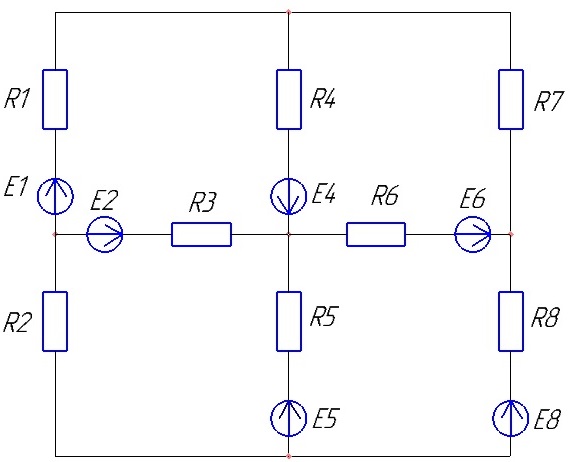
Рисунок 1 - Схема цепи постоянного тока

Для удобства дальнейших расчётов переведём проводимости в сопротивления по формуле:

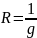
(1.1) [1 c.19]

где R - сопротивление, Ом;

g - проводимость, См;

Так как R2=∞, то оно является разрывом ветви, в которой находится.

Е1=Е4=Е6=Е8=0, следовательно, в цепи они являются перемычками, и цепь принимает следующий вид:

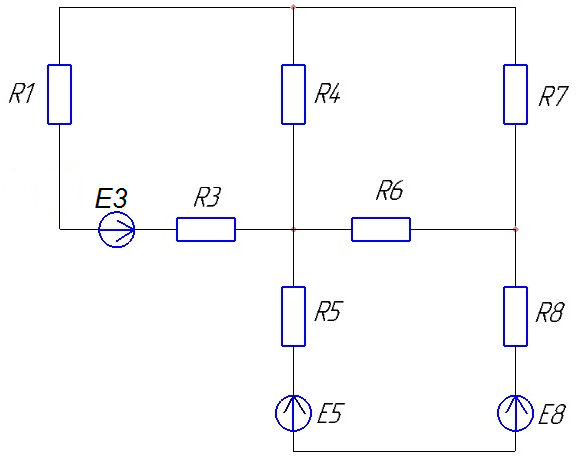
Рисунок 2 - Схема цепи, согласно исходных данных

2 Расчёт цепи методом законов Кирхгофа.

Метод расчёта цепи методом законов Кирхгофа основан на применении двух законов Кирхгофа:

- сумма подтекающих к любому узлу токов равна сумме утекающих от узла токов; [2, с.14]

- алгебраическая сумма ЭДС замкнутого контура равна алгебраической сумме падений напряжений в нём. [2, с.14]

Первый закон Кирхгофа в общем виде:

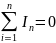
(2.1) [1, c.31]

Второй закон Кирхгофа в общем виде:

(2.2) [1, c.31]

Для расчёта цепи обозначим токи в ветвях, произвольно задав их направления, после чего выберем независимые контура, произвольно выбирая их направления обхода.

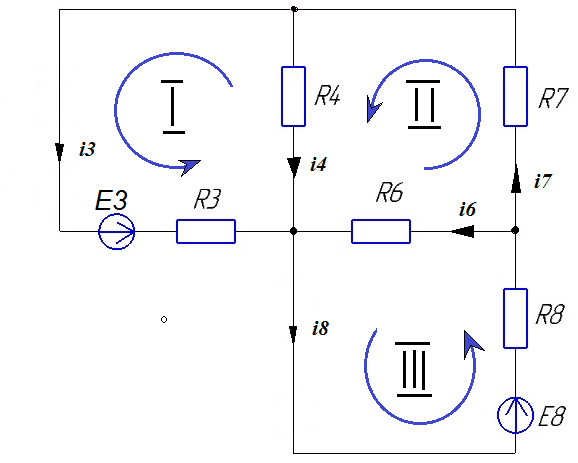
Рисунок 3 - Направления токов и обхода контуров

Для расчёта цепи постоянного тока методом законов Кирхгофа составляем (n-1) уравнений по первому закону Кирхгофа и [m-(n-1)] уравнений по второму закону Кирхгофа, где n - число узлов, а m - число искомых токов. Поэтому по первому закону составим два уравнения, а по второму - три.

По первому закону Кирхгофа:

По второму закону Кирхгофа:

На основе полученных уравнений составим матрицы А и В для дальнейшего решения в программе MathCAD:

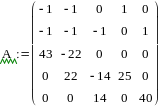
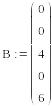
Путём умножения обратной матрицы А^-1 на матрицу В получим матрицу I c искомыми токами:

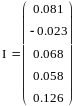
Таким образом I₃=0,081 А, I₄= –0.023 A, I₆=0,068 A, I₇= 0,058 A, I₈=0,126 A.

Проверка по балансу мощности производится путём сравнения мощности выделяемой источниками P_ист и мощности, потребляемой потребителями P_потр.

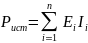
(2.3) [1, c.33]

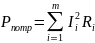
(2.4) [1, c.33]

Вычисления Р_потр и Р_ист были произведены в программе MathCAD. Р_потр=1.11 Вт, Р_ист=1.08 Вт

Рассчитаем погрешность:

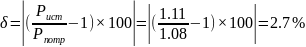
(2.5) [1, c.33]

Так как δ=2.7%, расчёт цепи выполнен верно.

3 Расчёт цепи методом контурных токов.

Расчёт цепи методом контурных токов позволяет ограничиться лишь решением системы уравнений по второму закону Кирхгофа. Для расчёта цепи данным методом требуется:

- выбрать произвольные направления токов во всех ветвях цепи;

- выбрать независимые контура и задать направления контурных токов;

- составить уравнения по второму закону Кирхгофа для контурных токов в том же количестве, что и для метода расчёта цепей по законам Кирхгофа.

Направления обхода контуров совпадают с направлениями контурных токов (Рисунок 3). Составляем уравнения по второму закону Кирхгофа.

На основе полученных уравнений составим матрицы А и В для дальнейшего решения в программе MathCAD:

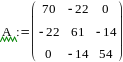
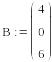
Путём умножения обратной матрицы А^-1 на матрицу В получим матрицу I c искомыми контурными токами:

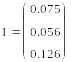
Таким образом I'=0,075 A, I''= 0,056 A, I'''=0,126 A.

Найдём токи в ветвях, с учётом того, что токи в ветвях дерева определяются как алгебраическая сумма контурных токов в ветви, а в ветвях связи токи по модулю равны токами контурным, и значение их зависит от совпадения направлений (при совпадении ток имеет положительное значение, если нет - отрицательное). [1, с.36-37]

I₃=I'=0,075 А

I₄=I'–I''=0,075–0,056= –0,019 А

I₆=I''' - I'' =0.126 - 0.056 = 0.07 А

I₇=I''= 0,056 А

I₈=I'''=0,126 А

Проверка по балансу мощности произведена в программе MathCAD согласно формулам 2.3, 2.4 и 2.5, погрешность δ=0.3%.

4 Расчёт цепи методом узловых потенциалов

Метод узловых потенциалов основан на том, что ток равен делению напряжения на сопротивление. В данном методе падение напряжения на пассивных элементах цепи представляется как разница потенциалов. [2, c.11, 21–22]

Направления токов расставлены согласно рисунку 1, узел №2 ­– заземлён.

Составим уравнения по первому закону Кирхгофа для узлов, которые не заземлены.

I₇-I₄–I₃=0

I₃+I₄+I₆ -I₈=0

Для упрощения дальнейших расчётов суммируем последовательные сопротивления и представляем сопротивления как проводимости согласно формулы 1.1.

Таким образом получаем g₃=0,02 См, g₄=0,045 См, g₆=0,071 См, g₇=0,04 См, g₈=0,025 См.

Представим токи в виде произведения разницы потенциалов и проводимости:

I₃=(φ₁–φ₂+E₃)*g₃

I₄=(φ₁–φ₂)*g₄

I₆=(φ₃–φ₂)*g₆

I₇=(φ₃–φ₁)*g₇

I₈=(φ₂–φ₃+E8)*g₈

Подставим получившиеся выражения в уравнения узловых токов. Для первого узла:

(φ₂–φ₁+E₁)*g₁₃+(φ₂–φ₁)*g₄–(φ₁–φ₃)*g₇=0

φ₁*(g₁₃+g₄+g₇)–φ₃*g₇=E1*g₁₃

φ₁*0,101– φ₃*0,018=0,364

Для второго узла:

(φ₃–φ₁)*g₇ - (φ₁–φ₂)*g₃–(φ₃–φ₂+E5–E8)*g₅₈=0

– φ₃(0,018+0,1+0,04)+ φ₁*0,018=(E5-E8)

– φ₃*0,158+ φ₁*0,018=0,04

На основе полученных уравнений составляем матрицы А и В для дальнейших расчётов в программе MathCAD.

Путём умножения обратной матрицы А-1 на матрицу В получим матрицу U c искомыми потенциалами:

Подставляя потенциалы в выражения токов, получим значения токов I₁=0,262 A, I₂= –0,202 A, I₃=0,062 A, I₄= –0,016 A, I₅=0,046 A.

Проверка по балансу мощности произведена в программе MathCAD согласно формулам 2.3, 2.4 и 2.5, погрешность составила δ=0,89%.

5 Расчёт цепи методом наложения

Ток в любой ветви линейной цепи можно рассматривать как алгебраическую сумму токов, создаваемых в этой ветви каждым источником в отдельности. На это основан метод наложения.

Для расчёта необходимо:

- произвольно расставить токи в ветвях;

- составить схемы замещения для каждого источника;

- рассчитать все схемы замещения, найти частичные токи;

- определить действительные токи как алгебраическую сумму частичных токов. [2, с.28]

Исходная схема представления на рисунке 3.

Начнём сворачивание схемы для источника E1.

Рассчитаем эквивалентное сопротивление R58 состоящее из сопротивлений R5 и R8. Так как R5 и R8 стоят последовательно друг с другом, то R58 считается по формуле:

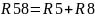
(5.1) [3]

Схема принимает вид:

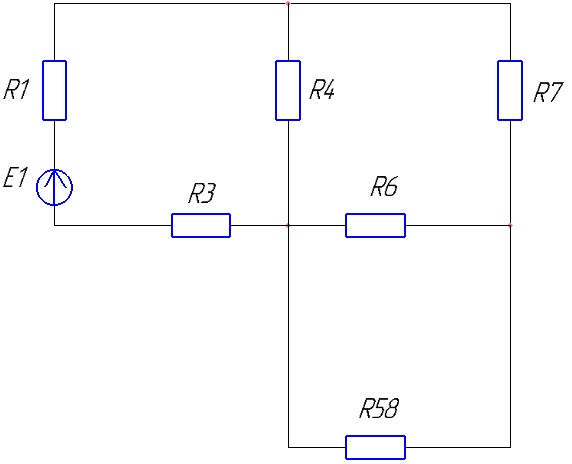
Рисунок 4 – Первый этап сворачивания цепи для первого источника ЭДС.

Далее рассчитываем эквивалентное сопротивление R586 из сопротивлений R6 и R58. Так как R6 и R58 находятся параллельно друг с

другом, то R586 считается по формуле:

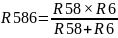
(5.2) [3]

Схема принимает вид:

Рисунок 4 – Второй этап сворачивания цепи для первого источника ЭДС.

Эквивалентное сопротивление R5867 состоит из последовательных сопротивлений R586 и R7, рассчитывается по формуле 5.1, и составляет:

R5867=62,698 Ом

Схема принимает вид:

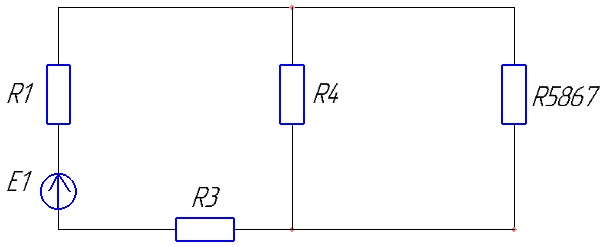
Рисунок 5 – Третий этап сворачивания цепи для первого источника ЭДС.

Эквивалентное сопротивление R58674 состоит из параллельных сопротивлений R5867 и R4, рассчитывается по формуле 5.2, и составляет:

R58674=13,985 Ом

Схема принимает вид:

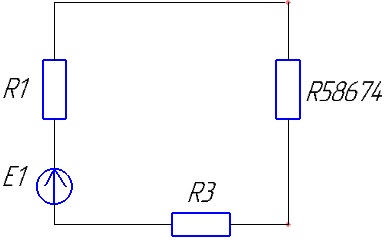
Рисунок 6 – Четвёртый этап сворачивания цепи для первого источника ЭДС.

Эквивалентное сопротивление Rэ состоит из последовательных сопротивлений R58674, R1 и R3, рассчитывается по формуле 5.1, и составляет:

Rэ=49,985 Ом

Схема принимает конечный вид:

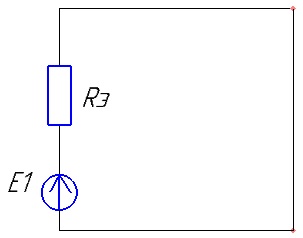
Рисунок 6 – Свёрнутая цепь для первого источника ЭДС.

Приступаем к расчёту частичных токов. При невозможности найти ток сразу, будем пользоваться законом Ома.

Примем E58 как эквивалент E5 и E8, так как они последовательно расположены в одной ветви. E58=E5–E8=1 B.

Свернём цепь относительно E58.

Эквивалентное сопротивление R13 состоит из последовательных сопротивлений R1 и R3, рассчитывается по формуле 5.1, и составляет:

R13=36 Ом

Схема принимает вид:

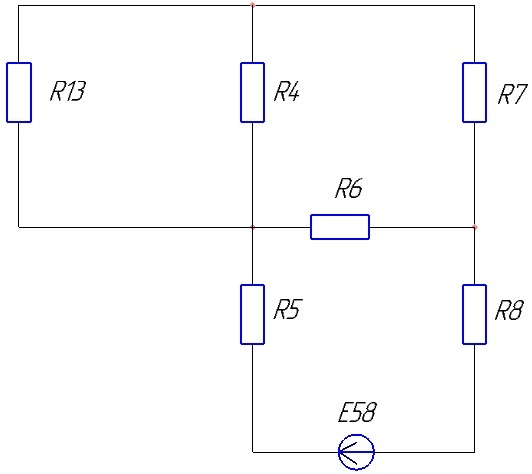
Рисунок 7 – Первый этап сворачивания цепи для второго источника ЭДС.

Эквивалентное сопротивление R134 состоит из параллельных сопротивлений R13 и R4, рассчитывается по формуле 5.2, и составляет:

R134=12 Ом

Схема принимает вид:

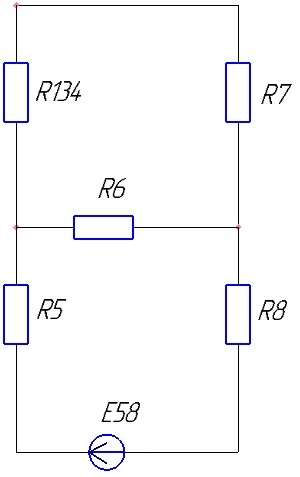
Рисунок 8 – Второй этап сворачивания цепи для второго источника ЭДС.

Эквивалентное сопротивление R1347 состоит из последовательных сопротивлений R134 и R7, рассчитывается по формуле 5.1, и составляет:

R1347=67,555 Ом

Схема принимает вид:

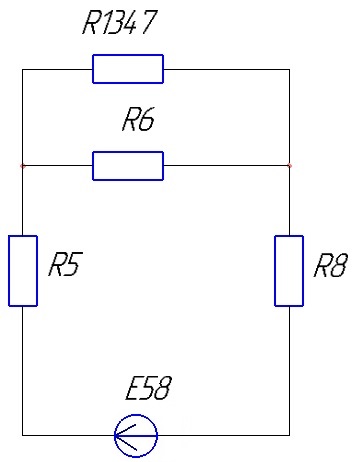
Рисунок 9 – Третий этап сворачивания цепи для второго источника ЭДС.

Эквивалентное сопротивление R13476 состоит из параллельных сопротивлений R1347 и R6, рассчитывается по формуле 5.2, и составляет:

R13476=8,711 Ом

Схема принимает вид:

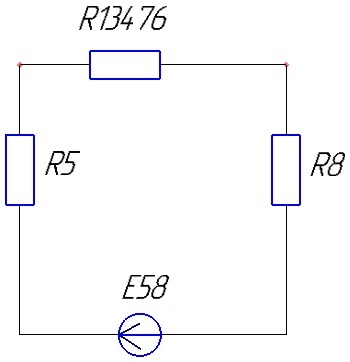
Рисунок 10 – Четвёртый этап сворачивания цепи для второго источника ЭДС.

Эквивалентное сопротивление Rэ₂ состоит из последовательных сопротивлений R13476, R5 и R8, рассчитывается по формуле 5.1, и составляет:

Rэ₂=33,711 Ом

Схема принимает конечный вид:

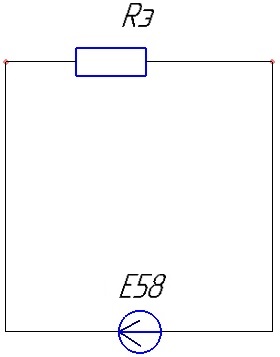
Рисунок 11 – Свёрнутая цепь для второго источника ЭДС.

Расчёт частичных токов для второго источника ЭДС аналогичен расчёту для первого источника.

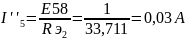
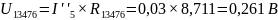
Рассчитаем истинные токи как алгебраическую сумму частичных токов.