4 сем учебник

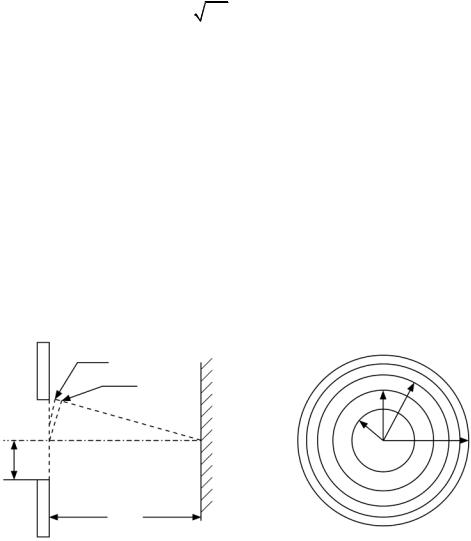
лишь центральной (первой) зоной Френеля. Таким образом, колебания, вызываемые в точке P волновой поверхностью F, имеют такую же амплитуду, как если бы действовала только половина первой (центральной) зоны.

Оценим размеры зон Френеля. Пусть дифракционная картина наблюдается на экране, расположенном на расстоянии L = 1 м от препятствия, а длина волны света λ = 600 нм (красный свет). Тогда радиус первой зоны Френеля

1 L 0,77 мм.

Следовательно, до точки наблюдения P свет распространяется как бы в узком канале, сечение которого равно половине первой (центральной) зоны Френеля, что соответствует прямолинейному распространению света.

Если на пути волны поставить диафрагму с отверстием, оставляющим открытым только центральную (первую) зону Френеля, амплитуда в точке P будет равна A1, что в два раза больше амплитуды, создаваемой всем волновым фронтом в отсутствие диафрагмы (A1/2). Соответственно интенсивность света в точке P при наличии диафрагмы будет в четыре раза больше, чем при ее отсутствии. Это не противоречит закону сохранения энергии – просто произошло ее перераспределение.

Дифракция на круглом отверстии и диске. Рассмотрим падение плоской световой волны на малое круглое отверстие радиусом R (рис. 1.21).

b Экран

В соответствии с методом зон Френеля плоский фронт, совпадающий с отверстием, разбиваем на кольцевые зоны Френеля. Если смотреть на волновую поверхность из точки P, то границы зон Френеля представляют собой концентрические окружности (рис. 1.22). Радиус k-й зоны Френеля был вычислен ранее. Он равен

30

k kb .

Число зон Френеля, укладывающихся в отверстии, определяется его радиусом R:

kR2 . b

Если число зон, которые укладываются в отверстии, четное, то в точке Р наблюдается темное пятно (волны от соседних зон приходят в точку Р в противофазе и попарно компенсируют друг друга).

При нечетном числе зон (k = 2n + 1) результирующая амплитуда коле-

баний

При небольших отверстиях (небольших k) амплитуды А1 и А2n+1 мало отличаются друг от друга, поэтому результирующая амплитуда

A A21 A22n 1 A1 ,

т. е. в точке P наблюдается светлое пятно.

Итак, если отверстие в непрозрачном экране оставляет открытой только одну зону Френеля, то амплитуда колебаний в точке наблюдения возрастает в два раза (соответственно интенсивность возрастает в четыре раза) по сравнению с действием невозмущенной волны. Если открыть две зоны, то амплитуда колебаний обращается в нуль. Если изготовить непрозрачный экран, который оставлял бы открытыми только несколько нечетных (или только несколько четных) зон, то амплитуда колебаний резко возрастет. Такие пластинки, обладающие свойством фокусировать свет, называются зонными пластин-

ками.

При дифракции света на круглом диске радиусом R закрытыми оказываются зоны Френеля первых номеров от 1 до k. При этом амплитуда колебаний в точке наблюдения

или

A = Ak+1/2,

31

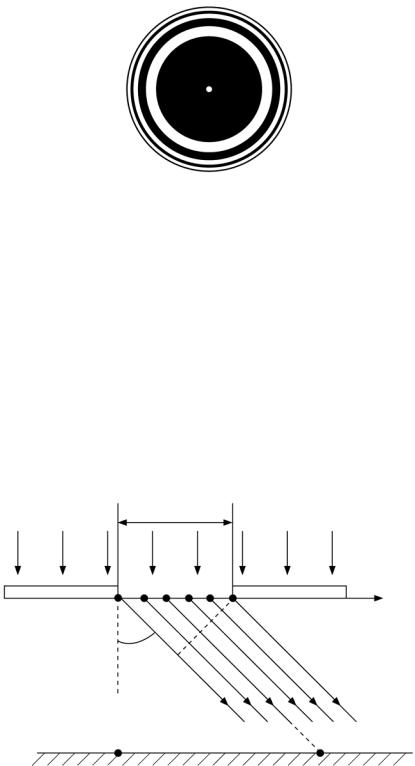
так как выражения, стоящие в скобках, равны нулю. Если диск закрывает зоны не со слишком большим номером, то в центре картины при дифракции света на диске наблюдается интерференционный максимум (рис. 1.23).

Рис. 1.23

Расчет амплитуды результирующих колебаний, пришедших в другие точки экрана, более сложен. Согласно симметрии интерференционная картина на экране вокруг центрального светлого (или темного) пятна должна иметь вид чередующихся светлых и темных колец с центром в точке Р.

Дифракция света на щели. Пусть на бесконечную длинную щель падает плоская световая волна. Дифракционная картина наблюдается на экране, расположенном в фокальной плоскости собирающей линзы, установленной за щелью (на рис. 1.24 линза не изображена). В соответствии с принципом Гюйгенса–Френеля освещенную щель можно рассматривать как множество точечных когерентных источников волн. Благодаря линзе в точке Р экрана собирается параллельныйпучок лучей, отклонившийся науголφ (рис. 1.24).

a

C

Рис. 1.24

32

Разность хода AC крайних лучей из этого пучка находим из треугольника ABC, а именно,

asin ,

где а = |AB| – ширина щели. Если при наблюдении из точки Р в щели помещается четное число зон Френеля, то их вклады взаимно погасятся и в точке Р будет наблюдаться минимум интенсивности света. Таким образом, уравнение

asin mink k , k = 1, 2, 3, …,

есть условие дифракционных минимумов, в котором угол mink направлен на

минимум с номером k.

Рассуждая аналогично, приходим к условию дифракционных макси-

мумов

Отметим, что в направлении = 0 щель действует как одна зона Френеля, и в этом направлении свет распространяется с наибольшей интенсив-

ностью, т. е. в центре наблюдается центральный дифракционныймаксимум.

Дифракционная решетка. Явление дифракции используется для спектрального анализа и точного измерения длин волн. Для этой цели применяются дифракционные решетки. Они представляют собой периодические структуры, выгравированные специальной делительной машиной на поверхности стеклянной (решетки на просвет) или металлической (решетки на отражение) пластинки (рис. 1.25). Простейшая дифракционная решетка состоит из N одинаковых щелей шириной b каждая, отделенных друг от друга непрозрачными промежутками шириной а (рис. 1.26). Величина d a b

называется периодом решетки.

O Л

Э

33

Если на дифракционную решетку перпендикулярно ее поверхности падает пучок параллельных световых лучей, то в соответствии с принципом Гюйгенса–Френеля каждая щель представляет собой совокупность вторичных источников когерентных волн, способных интерферировать друг с другом. Интерференция волн осуществляется с помощью собирающей линзы Л, в главной фокальной плоскости которой на экране Э наблюдается интерференционная картина – чередование максимумов и минимумов света.

В точке F0 соберутся все лучи, направленные под углом 0 0 , кото-

рые образуют максимум нулевого порядка.

Интенсивность света в точке Fφ является результатом интерференции вторичных волн, приходящих в эту точку от N щелей. Для того чтобы в точке Fφ наблюдался интерференционный максимум, разность хода между волнами, исходящими из соседних щелей, должна быть равна целому числу длин волн:

d sin k , k = 0, ±1, ±2, ...

Вточках экрана, для которых это условие выполнено, располагаются так называемые главные максимумы дифракционной картины. В эти макси-

мумы все волны приходят в одинаковой фазе, поэтому амплитуда колебаний возрастает в N раз (амплитуды складываются), а интенсивность – в N2 раз по сравнению с колебаниями, которые возбуждает световая волна, пришедшая только от одной щели.

Из формулы дифракционной решетки следует, что положение главных максимумов кроме нулевого (k = 0) зависит от длины волны λ. Таким образом, решетка способна разлагать излучение в спектр, т. е. она может слу-

жить спектральным прибором.

Если на решетку падает немонохроматическое излучение, то в каждом порядке дифракции (т. е. при каждом значении k) возникает спектр исследуемого излучения, причем фиолетовая часть его располагается ближе к максимуму нулевого порядка. Максимум нулевого порядка остается неокрашенным.

1.5.Взаимодействие света с веществом

Дисперсия света. Дисперсией света называется зависимость абсолютного показателя преломления среды n от частоты (длины волны) падающего на среду света.

Так как показатель преломления n зависит от скорости света v в данной среде (n c / v , где с – скорость света в вакууме), дисперсию света можно рассматривать как зависимость показателя преломления от скорости света в данной среде.

34

Явление дисперсии экспериментально обнаруживается при прохождении немонохроматического белого света (т. е. света, представляющего собой совокупность волн с разной длиной) через призму (рис. 1.27). При этом на экране MN , находящемся позади призмы, наблюдается радужная картина, состоящая из разных плавно переходящих друг в друга цветов, каждому из которых соответствует определеннаядлинаволны, или частота. Совокупность длин волн (частот), из которых состоит немонохроматическое излучение, называется спектром. Спектр видимого света занимает на шкале электромаг-

нитных волн участок от 7,5 10 7 (красный свет) до 3,9 10 7 м (фиолетовый свет).

Характер спектра зависит от рода вещества, испускающего световые волны:

а) раскаленные твердые тела и светящиеся жидкости создают непрерывные спектры, которые представляют собой набор длин волн (частот), плавно переходящих друг в друга;

б) светящиеся сильно разреженные газы, содержащие одиночные атомы, создают линейчатые спектры, которые состоят из отдельных спектральных линий, разделенных темными промежутками;

в) излучающие молекулы создают полосатые спектры, которые представляют собой множество тесно расположенных спектральных линий, образующих полосы, разделенные темными промежутками.

С помощью спектров испускания вещества можно определять его химический состав и концентрацию атомов (или молекул). Совокупность методов, с помощью которых производятся такие исследования, называется спек-

тральным анализом.

Классическая электронная теория дисперсии. Согласно электромаг-

нитной теории Максвелла показатель преломления электромагнитных волн

n .

35

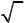
Поскольку для всех диэлектриков с высокой степенью точности μ = 1, показатель преломления

n .

Классическая электронная теория Г. Лоренца рассматривает дисперсию света как результат вынужденных колебаний электронов, входящих в состав атома, под действием поля электромагнитной волны. Вектор напряженности электрического поля, совершающий колебания по закону

E = E0cosωt,

заставляет электроны совершать вынужденные колебания под действием двух сил – силы упругости

Fупр kl m 02l

(k – жесткость связи электрона в атоме, l – отклонение его от положения равновесия, m – масса электрона, ω0 – его собственная частота колебаний) и внешнейсилы

F eE eE0cosωt.

По второму закону Ньютона

F Fупр ma,

где a d 22l – ускорение электрона. dt

Подстановка сил упругости и внешней силы во второй закон Ньютона дает уравнение вынужденных колебаний

d 2l 2l eE0 cos t. dt2 0 m

Решение данного дифференциального уравнения (в чем можно убедиться простой подстановкой) имеет вид

Таким образом, под действием электромагнитного поля электрон внутри атома или молекулы совершает вынужденные колебания. При этом у молекулы (атома) появляется переменный дипольный момент

36

Как следует из элементарной теории, диэлектрическая проницаемость среды определяется отношением суммы дипольных моментов, наведенных электрическим полем у молекул (атомов) вещества, к напряженности электрического поля:

1 Np .

0 E

Здесь N – концентрация молекул.

Подставляя в это выражение значение дипольного момента p, получаем закон дисперсии:

n2

1,5

1

0,5

ω0 ω

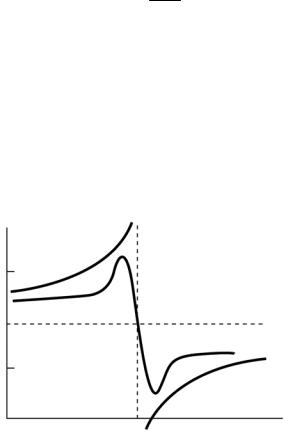
Рис. 1.28

Теоретическая и экспериментальная зависимости n2 от циклической частоты света ω приведены на рис. 1.28. Теоретическая зависимость имеет разрыв при совпадении частоты электромагнитной волны с собственной частотой колебаний электронов.

Согласно рис. 1.28 вдали от собственной частоты колебаний электрона (при ω ≠ ω0) теоретическая и экспериментальная кривые хорошо совпадают. Эта область, где показатель преломления возрастает с возрастанием частоты, называется областью нормальной дисперсии.

Вблизи собственной частоты ω0 рассмотренная упрощенная теория не применима. В этой области необходимо учитывать затухание колебаний (поглощение света). В результате вблизи ω0 показатель преломления уменьшается с увеличением частоты ω (см. рис. 1.28). Такой ход зависимости n от ω называется аномальной дисперсией.

37

Дисперсия присуща всем средам кроме абсолютного вакуума.

Итак, показатель преломления вещества имеет разное значение для разных частот (длин волн) электромагнитного излучения. Именно поэтому во многих случаях недостаточно привести значение показателя преломления вещества. Необходимо указать, какому диапазону длин волн он соответствует. Например, для воды ε = 81, а n2 = 1,75 (здесь диэлектрическая проницаемость определена для статических полей, а показатель преломления – для пе-

ременногоэлектромагнитногополяоптическогодиапазона, т. е. 1014 Гц). Примером дисперсии света является радуга. Ее можно видеть, если Солнце находится за спиной наблюдателя. Лучи красного и фиолетового света преломляются сферическими капельками воды и отражаются от их внутренней поверхности. Лучи красного света преломляются меньше и попадают в глаз наблюдателя от капелек, находящихся на большей высоте. Поэтому

верхняяполоса радуги всегда оказывается красной.

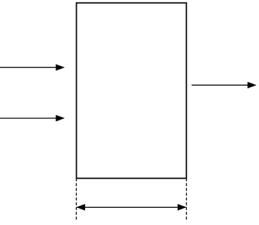
Поглощение света. Закон Бугера–Ламберта–Бера. По мере распро-

странения световой волны в веществе ее интенсивность уменьшается, так как часть энергии идет на возбуждение колебаний электронов среды. Эта энергия колебаний, в свою очередь, переходит в энергию движения атомов, т. е. в тепловую энергию. Явление уменьшения энергии световой волны, проходящей через вещество, называется поглощением (абсорбцией) света.

Опыт показывает, что интенсивность света после прохождения слоя вещества толщиной х убывает по экспоненциальному закону:

I I0e k x ,

где I0 – интенсивность падающего света; I – интенсивность света, прошедшего слой вещества; k – коэффициент поглощения, зависящий от длины волны света, а также от химической природы и состояния поглощающего вещества

(рис. 1.29). Эта формула есть закон Бугера–Ламберта.

x

Рис. 1.29

38

Зависимость коэффициента поглощения k от длины волны λ определяет спектр поглощения вещества. Для изолированных атомов (например, в разреженных газах) спектр поглощения имеет вид набора узких линий, т. е. коэффициент поглощения отличен от нуля лишь в определенных, узких, диапазонах длин волн. Эти диапазоны соответствуют частотам собственных колебаний электронов внутри атомов, которые находятся в резонансе с проходящим излучением и поэтому поглощают энергию световой волны. Спектры поглощения молекул занимают существенно более широкие области длин волн – это так называемые полосы поглощения. Наконец, поглощение света жидкостями и твердыми телами обычно характеризуется очень широкими областями с большими значениями коэффициента поглощения. Качественно это объясняется тем, что сильное взаимодействие между частицами жидкостей и твердых тел приводит к быстрой передачепоглощенной энергии всему коллективу частиц. Другими словами, со световой волной находятся в резонансе не только отдельныечастицы, но и многочисленныесвязи между ними. Об этом свидетельствует изменение поглощения света газами с увеличением давления – чем выше давление (чем сильнее взаимодействие частиц), тем шире полосы поглощения, которые при высоких давлениях становятся похожи на спектры поглощения жидкостей.

Если поглощающее вещество растворено в прозрачном растворителе, то коэффициент поглощения k раствора пропорционален концентрации растворенного вещества с, т. е.

k( ) ( )N.

Здесь ε(λ) – постоянная, характернаядля каждоговещества, называемая эффективным сечением поглощения. Она определяет спектр поглощения отдельной молекулы.

Объединенная формула, описывающая поглощение света раствором,

I I0e Nx

носит название закона Бугера–Ламберта–Бера.

Поглощение света используется в разных областях науки и техники. На нем основаны высокочувствительные методы количественного и качественного химического анализа, так как эффективное сечение поглощения ε(λ) однозначно связано с химической структурой вещества.

1.6. Поляризация света

Виды поляризации световой волны. Электромагнитные волны в ва-

кууме поперечны: векторы напряженности электрического и магнитного по-

39