ТЗ-7 Федорова В. Т-910
.pdf
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ЖЕЛЕЗНОДОРОЖНОГО ТРАНСПОРТА
Федеральное государственное бюджетное образовательное учреждение высшего образования
“ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ПУТЕЙ СООБЩЕНИЯ ИМПЕРАТОРА АЛЕКСАНДРА I”
(ФГБОУ ВО ПГУПС)
Факультет «Промышленное и гражданское строительство» Кафедра «Водоснабжение, водоотведение и гидравлика»
Дисциплина «Гидравлика и гидрология» Форма обучения - очная
ТИПОВАЯ ЗАДАЧА № 7
«ВЫЧИСЛЕНИЕ РАСЧЁТНОГО РАСХОДА ПРИ ДОСТАТОЧНОЙ ПРОДОЛЖИТЕЛЬНОСТИ НАБЛЮДЕНИЙ»
Выполнил(а) Группа Т-910 Курс II
Факультет: «Транспортное строительство»
Преподаватель:
(подпись, дата)
Фёдорова В.Ю.
(ФИО)
Пономарёв А.Б.
(ФИО преподавателя)
Показатель |
Критерии оценивания |
Шкала |
Итоговая |
|
оценивания |
оценивания |
оценка |
||
|
||||
Оформление в |
Работа оформлена аккуратно без исправлений |
0 |
|
|
соответствии с |
|
|
|
|
Работа оформлена неаккуратно, есть исправления |
-1 |
|
||
требованиями |
|
|||
|
|
|
|
|
Правильность |
Задача решена верно |
4 |
|
|
решения задачи |
Задача решена неверно |
0 |
|
|
|
|
|
|
|
Сроки сдачи |
Работа сдана в течение 2 недель после выдачи задания на занятии |
1 |
|
|
Работа сдана более, чем через 2 недели после выдачи задания на занятии |
|
|
||
работы |
0 |
|
||
(при отсутствии уважительных причин) |
|
|||
|
|
|
||
|
|
|
|
|
Итого баллов |
|
Максимум |
|
|
|
5 |
|
||
|
|
|
||
|
|
|
|
Санкт-Петербург, 2021
Ряды максимальных расходов Qi, м3/с
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
Река А, xi, Река В, xi,м3/с
1972 |
171 |
|
1973 |
275 |
|
1974 |
466 |
|
1975 |
135 |
|
1976 |
227 |
|
1977 |
292 |
|
1978 |
205 |
|
1979 |
416 |
|
1980 |
90 |
|
1981 |
265 |
|
1982 |
202 |
|
1983 |
324 |
|
1984 |
362 |
|
1985 |
220 |
|
1986 |
286 |
|
1987 |
340 |
|
1988 |
193 |
|
1989 |
367 |
|
1990 |
382 |
|
1991 |
151 |
|
1992 |
268 |
137 |
1993 |
331 |
207 |
1994 |
184 |
103 |
1995 |
230 |
131 |
1996 |
308 |
205 |
1997 |
76 |
40 |
1998 |
229 |
113 |
1999 |
349 |
225 |
2000 |
178 |
97 |
2001 |
236 |
142 |
2002 |
279 |
164 |
|
|
|
Среднее а |
259.2581 |
|
p=(m/n+1)*100%
|
m |
Qi в убыва |
Ki |
|
Ki -1 |
(Ki-1)^2 |
(Ki-1)^3 |
p, % |
|
lg Ki |
Ki*lg Ki |
|
|
Точность |
|
0.01 |
0.01 |
0.001 |
0.0001 |
|
0.1 |
0.001 |
0.001 |
|
1 |
466 |
|
1.80 |
0.80 |
0.640 |
0.5120 |
|
3.1 |
0.255 |
0.458 |
|
2 |
416 |
|
1.60 |
0.60 |
0.360 |
0.2160 |
|
6.3 |
0.205 |
0.330 |
|
3 |
382 |
|
1.47 |
0.47 |
0.221 |
0.1038 |
|
9.4 |
0.168 |
0.248 |
|
4 |
367 |
|
1.42 |
0.42 |
0.176 |
0.0741 |
|
12.5 |
0.151 |
0.214 |
|
5 |
362 |
|
1.40 |
0.40 |
0.160 |
0.0640 |
|
15.6 |
0.145 |
0.202 |
|
6 |
349 |
|
1.35 |
0.35 |
0.123 |
0.0429 |
|
18.8 |
0.129 |
0.174 |
|
7 |
340 |
|
1.31 |
0.31 |
0.096 |
0.0298 |
|
21.9 |
0.118 |
0.154 |
|
8 |
331 |
|
1.28 |
0.28 |
0.078 |
0.0220 |
|
25.0 |
0.106 |
0.135 |
|
9 |
324 |
|
1.25 |
0.25 |
0.063 |
0.0156 |
|
28.1 |
0.097 |
0.121 |
|
10 |
308 |
|
1.19 |
0.19 |
0.036 |
0.0069 |
|
31.3 |
0.075 |
0.089 |
|
11 |
292 |
|
1.13 |
0.13 |
0.017 |
0.0022 |
|
34.4 |
0.052 |
0.058 |
|
12 |
286 |
|
1.10 |
0.10 |
0.010 |
0.0010 |
|
37.5 |
0.043 |
0.047 |
|
13 |
279 |
|
1.08 |
0.08 |
0.006 |
0.0005 |
|
40.6 |
0.032 |
0.034 |
|
14 |
275 |
|
1.06 |
0.06 |
0.004 |
0.0002 |
|
43.8 |
0.026 |
0.027 |
|
15 |
268 |
|
1.03 |
0.03 |
0.001 |
0.0000 |
|
46.9 |
0.014 |
0.015 |
|
16 |
265 |
|
1.02 |
0.02 |
0.000 |
0.0000 |
|
50.0 |
0.010 |
0.010 |
|
17 |
236 |
|
0.91 |
-0.09 |
0.008 |
-0.0007 |
|
53.1 |
-0.041 |
-0.037 |
|
18 |
230 |
|
0.89 |
-0.11 |
0.012 |
-0.0013 |
|
56.3 |
-0.052 |
-0.046 |
|
19 |
229 |
|
0.88 |
-0.12 |
0.014 |
-0.0017 |
|
59.4 |
-0.054 |
-0.048 |
|
20 |
227 |
|
0.88 |
-0.12 |
0.014 |
-0.0017 |
|
62.5 |
-0.058 |
-0.051 |
|
21 |
220 |
|
0.85 |
-0.15 |
0.023 |
-0.0034 |
|
65.6 |
-0.071 |
-0.061 |
|
22 |
205 |
|
0.79 |
-0.21 |
0.044 |
-0.0093 |
|
68.8 |
-0.102 |
-0.081 |
|
23 |
202 |
|
0.78 |
-0.22 |
0.048 |
-0.0107 |
|
71.9 |
-0.108 |
-0.084 |
|
24 |
193 |
|
0.74 |
-0.26 |
0.068 |
-0.0176 |
|
75.0 |
-0.128 |
-0.095 |
|
25 |
184 |
|
0.71 |
-0.29 |
0.084 |
-0.0244 |
|
78.1 |
-0.149 |
-0.106 |
|
26 |
178 |
|
0.69 |
-0.31 |
0.096 |
-0.0298 |
|
81.3 |
-0.163 |
-0.112 |
|
27 |
171 |
|
0.66 |
-0.34 |
0.116 |
-0.0393 |
|
84.4 |
-0.181 |
-0.119 |
|
28 |
151 |
|
0.58 |
-0.42 |
0.176 |
-0.0741 |
|
87.5 |
-0.235 |
-0.137 |
|
29 |
135 |
|
0.52 |
-0.48 |
0.230 |
-0.1106 |
|
90.6 |
-0.283 |
-0.148 |
|
30 |
90 |
|
0.35 |
-0.65 |
0.423 |
-0.2746 |
|
93.8 |
-0.459 |
-0.160 |
|
31 |
76 |
|
0.29 |
-0.71 |
0.504 |
-0.3579 |
|
96.9 |
-0.533 |
-0.156 |
|
Сумма Q |
8037 |
|
|
0.01 |
3.852 |
0.1339 |
|
|
-0.993 |
0.877 |
|
|
|
|
|
4.49 |
|
|
|
|
|
|
|
|
|
|
|
-4.48 |
|
|
|
|
|
|
Проверка: 1% < 5%
а) МЕТОД МОМЕНТОВ |
|
|
|
|
|
|
|
|
|
|
||
|
|
Коэффицент вариации Cv= |
0.36 |
|
|
Cs/Cv = 0,103 |
|
|
|
|||
|
|
Коэффициент ассиметрии Сs= |
0.037 |
|
|
Cs = 0,103Cv |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
p, % |
0.1 |
0.3 |
1 |
3 |
|
5 |
10 |
25 |
|
50 |
75 |
95 |
K |
2.1 |
1.99 |
1.84 |
1.68 |
|
1.6 |
1.5 |
1.24 |
|
0.99 |
0.752 |
0.44 |
Q, м3/с |
544 |
516 |
477 |
436 |
|
415 |
389 |
321 |
|
257 |
195 |
114 |
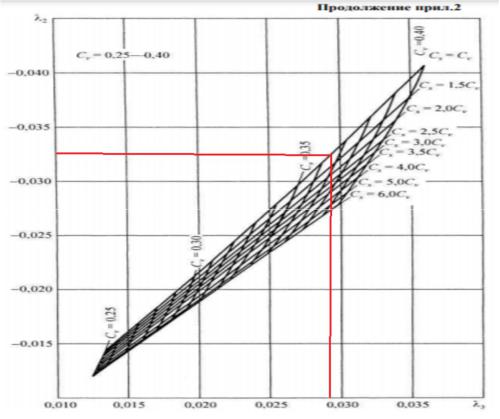
б) МЕТОД НАИБОЛЬШЕГО ПРАВДОПОДОБИЯ
λ2 = |
-0.033 |
λ3 = |
0.029 |
По номограмме (прил. 2) определили
Сv= 0,36 Cs/Cv = 1
Cs = (Cs/Cv)*Cv = 1*0,36 = 0,36
p, % |
0.1 |
0.3 |
1 |
3 |
5 |
10 |
25 |
50 |
75 |
95 |
K |
2.4 |
2.225 |
2.03 |
1.82 |
1.71 |
1.54 |
1.26 |
0.97 |
0.7 |
0.39 |
Q, м3/с |
622 |
577 |
526 |
472 |
443 |
399 |
327 |
251 |
181 |
101 |
Q, М3/С
Кривая обеспеченности
Кривые обеспеченности
700
600
500
400
300
200
100
0
P, %
0.1 |
0.3 |
1 |
3 |
5 |
10 |
25 |
50 |
75 |
95 |
Метод сравнения 
Метод наибольшего правдоподобия 
Эмпирическая
В качестве расчетного максимального расхода принимаем наибольшее значение из вычисленных методами моментов и наибольшего правдоподобия:
а) метод моментов Q1% = 477 м3/c
б) метод наибольшего правдоподобия Q1% = 526 м3/c
таким образом, Q1% = 526 м3/c
ОТВЕТ: Q1% = 526 м3 /c