2. Информационная энтропия

Определений информационной энтропии несколько:

1. Мера неопределенности некоторой системы, в частности непредсказуемость появления какого-либо символа базового алфавита. Это определение является прямым аналогом понятия энтропия, которая используется в статической термодинамике

2. Средняя скорость генерирования значений некоторым случайным источником данных

Например, в последовательности букв, составляющих какое-либо предложение на русском языке, разные буквы появляются с разной частотой. Поэтому неопределенность появления для некоторых букв будет меньше, чем для других. А если учесть, что некоторые сочетания букв встречаются очень редко, то неопределенность уменьшается еще сильнее.

2.1 Формула Хартли

В 1928 году Ральф Хартли предложил формулу, с помощью которой можно было измерить количество информации в сообщении. Формула Хартли является логарифмической мерой информации и имеет вид:

,

где:

• N – количество символов в используемом алфавите (мощность алфавита)

• K – длина сообщения (количество символов в сообщении)

• I – количество информации в сообщении

Из данной формулы можно сделать вывод, что с помощью алфавита, состоящего из одного символа, нельзя передать сообщение, так как количество информации для него будет равно

Данная формула применима к задачам, в которых вероятность сообщений равна. Например, если необходимо угадать число из набора чисел от одного до ста, то можно сказать, что сообщение о верно угаданном числе будет содержать приблизительно

Величины измерения в данной формуле как таковой нет, поэтому обычно результат обозначают в «единицах информации».

Однако, если вероятность сообщений различна, то формула Хартли не работает. Данной проблемой занялся Клод Шеннон в своих работах 1948 года.

2. Энтропия Шеннона

До работ Шеннона по данной теме понятие «энтропия» в отношении количественной оценки информации не употреблялось. В сформировавшейся после этого теории информации за понятием энтропия стоит идея о том, информационная ценность переданного сообщения зависит от степени того, насколько информация о событии является «неожиданной». Если вероятность события высока, то нет «неожиданности» в том, что оно совершилось – значит, сообщение о таком событии не представляет интереса и несет меньше информации. С другой стороны, если событие маловероятно, то получение сообщения о том, что оно произошло, является более информативным. Примером такого сообщения может быть информация о лотерейных билетах. Если будет получено сообщение о том, что какой-то конкретный билет является проигрышным, то количество информации в нем будет низкой, так как вероятность данного события очень высока. И напротив, имея сообщение о выигрышном лотерейном билете, человек получает информацию высокой ценности, так как это событие с крайне низкой вероятностью.

Информационное содержание события выражается следующей формулой:

,

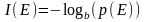где:

• E – определенное событие

• p(E) – вероятность данного события

• b – основание логарифма

Например, с помощью данной формулы можно сделать вывод, что результат подбрасывания «правильной» кости, где вероятность выпадения каждой грани равна 1/6, несет в себе больше информации, чем результат подбрасывания монеты.

Основание логарифма для каждой конкретной задачи может быть различной, однако чаще всего используется основание 2. Результат логарифмирования по основанию 2 был назван бит или шеннон. Если логарифм является натуральным (имеет основанием число Эйлера), то такой результат измеряется в натах, а при основании логарифма 10 – дитами или хартли.

Шеннон также определил энтропию сообщения как математическое ожидание информационного содержания дискретной случайной величины:

,

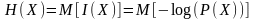где:

• М – оператор математического ожидания

• X – дискретная случайная величина, принимающая значения {x₁, x₂..,x_n}

• P(X) – функция вероятности дискретной случайной величины X

• I – информационное содержание X

После раскрытии операторов формула принимает вид:

Особый случай функции энтропии называется функцией бинарной энтропии. В теории информации - это энтропия процесса с распределением вероятности Бернулли. Эксперимент проводится с условием, что случайная величина X принимает одно из двух возможных значений. Вероятность первого исхода принимается за p, а второго за 1-p. Соответственно, формула для энтропии такого процесса принимает вид:

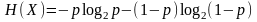
В данном случае 0*log₂0 принимают равным 0. Данный процесс можно проиллюстрировать подбрасыванием различных монет. Если монета сбалансирована, то вероятность выпадения любой из сторон будет равна 1/2. Это ситуация максимальной неопределенности и самая сложная для предсказания. Результат каждого подбрасывания будет содержать полный шеннон (или бит) информации. Однако, если известно, что монета сбалансирована в одну из двух сторон больше, то вероятности p и 1-p не будут равны. Сниженная неопределенность ведет к снижению энтропии – в среднем каждый такой бросок будет нести менее 1 шеннона информации. Например, если p = 0.7, тогда:

Г рафик функции бинарной энтропии представлен на рисунке 1.

Рисунок 1. График функции бинарной энтропии