
Пособие в_3_20
.pdfЛабораторная работа 3. Методы многомерного поиска Задачи безусловной оптимизации
При решении задачи оптимизации вида
X x1 , x2 , ..., xn , в которых целевая функция нелинейна и ограничения
отсутствуют, могут применяться методы прямого поиска, градиентные методы (первого порядка) и второго порядка. Методы прямого поиска – это методы, вычисляющие и минимизирующие F X без ее дифференцирова-
ния (программная функция fminsearch в MATLAB Optimization Toolbox). Методы первого и второго порядка используют информацию о градиенте целевой функции или о производных второго порядка (надстройка «Поиск решения» MS Office Excel или программная функция fminunc в MATLAB Optimization Toolbox). Методы прямого поиска об-
ладают хорошей устойчивостью и позволяют исследовать недифференцируемые функции. Методы на основе вычисления производных позволяют повысить скорость поиска оптимума, но накладывают ряд условий на вид целевой функции.
Методы прямого поиска
В MATLAB Optimization Toolbox прямой поиск реализован функцией fminsearch, которая использует модификацию симплекс-метода (ме-
тод Нелдера-Мида). В CAD/CAE-системе SolidWorks/CosmosWorks для параметрической оптимизации конструкций применяется тот же метод. Для изложения идеи метода Нелдера-Мида вначале будет проиллюстрирован метод регулярного симплекса, а затем – метод деформируемого многогранника.
Метод регулярного симплекса
Метод поиска экстремума с помощью регулярного симплекса получил свое название за счет использования регулярной (равносторонней) фигуры в n -мерном пространстве Регулярный многогранник называется симплексом. Для вектора переменных X x1 , x2 , ..., xn , симплекс в n -мерном
пространстве описывается n 1 вершинами. В двумерном пространстве проектирования симплекс представляет собой равносторонний треугольник, в трехмерном – тетраэдр.
На каждом шаге поиска рассчитывается новая точка решения внутри или вблизи симплекса. Значение функции в новой точке сравнивается со значениями функции в вершинах симплекса, и, как правило, одна из вершин заменяется новой точкой, образуя новый симплекс. Процедура повто-

ряется до тех пор, пока размер симплекса не станет меньше заданной погрешности вычислений. По сравнению с градиентными методами, в ряде случаев симплекс-метод является более устойчивым.
При поиске минимума целевой функции f x двух переменных в каче-
стве симплекса используется равносторонний треугольник. Первоначально векторы входных параметров задают в вершинах симплекса, где и вычисляют значения целевой функции. далее определяют, в какой вершине симплекса целевая функция имеет максимальное значение. Затем определяют центр тяжести симплекса (в данном случае центр равностороннего треугольника) и отображают вершину с максимальным значением целевой функции через центр тяжести (рис. 2).
Строят новый регулярный симплекс, вершинами которого будут две вершины предыдущего симплекса и отображенная вершина. В отображенной вершине вычисляют значение целевой функции, и процесс повторяется. Таким образом, шаг за шагом регулярный симплекс перемещается в сторону минимума. дополнительно предусмотрены правила уменьшения размера симплекса и предотвращения циклического движения вокруг точки экстремума.
Исходный симплекс имеет вершины а, b и с. В вершине а значение целевой функции имеет максимальное значение. Вершина а через центр тяжести отображается, и таким образом, получена отображенная вершина d. Отображенный симплекс имеет вершины b, с и d (рис. 2). Поиск экстремума заключается в последовательном отображении вершины симплекса и его сжатии (уменьшении размера симплекса). Траектория поиска экстремума целевой функции показана на рис. 3. для уточнения точки экстремума на последнем шаге надо выполнить сжатие симплекса (на рис. 3 не показано).
Алгоритм метода регулярного симплекса.
1.Задать координаты x1,1 и x1,2 стартовой (базовой) точки. Для n-мерного случая — п координат.
2.Задать длину ребра (b) регулярного симплекса.
3.Вычислить координаты вершин симплекса по формулам:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
1 |
|
1 |
|
|
|||||
|
|
x1,1 |
|
|
|
|
b, |
j i |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
i, j |
|
|
|
|
|
n 2 |
|
|||||||
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n 1 |
n 1 |
|
||||||||
|
|
x1,2 |
|
|
|
b, |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
n 2 |
|
|||||||
|
|
|
|
|
|
|
|
||||||||
4. В каждой вершине симплекса
L(х).
, i 2, n 1
j i
определить значение целевой функции
2

5. |
|
Вычислить |
|
критерий |
останова |
алгоритма |
по |
формуле: |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
1 |
|
L xi L xn 2 |
2 |
, где - малое число. |
|
|
|
||
|
n 1 |
|
|
|
||||||
|
i 1 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
Если критерий останова алгоритма меньше , то перейти к шагу 13. Если «нет», то перейти к шагу 6.
6.Определить вершину с максимальным значением целевой функции и присвоить ей индекс h, т.е. L(хh) Определить вершину с минимальным значением целевой функции и присвоить ей индекс l, т.е. L(хl)
7.Вычислить координаты центра тяжести (порядковый номер вершины
п+ 2) по формуле:
|
|
|
1 |
n 1 |
|
|
|
|
n 2, j |
|
|
|
|
|
i, j |
x |
|
|
n |
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
i 1 |
|
|
|
|
|
|
xh, j . |
|
|
|
|
8.Отобразить вершину хh через центр тяжести, т. е. пересчитать коор-
динаты вершины (порядковый номер отображенной вершины п + 3) по формуле: xn 3, j xn 2, j xn 2, j xh, j , где - коэффициент отображения.
9.Вычислить значение целевой функции в отображенной вершине.
10.Если значение целевой функции в отображенной вершине меньше чем в вершине хh, то заменить вершину хh симплекса на отображенную вершину. Если «нет», то перейти к шагу 11.
11.Выполнить редукцию (сжатие к вершине хl симплекса) симплекса по формуле: xi, j xl, j ,i l,i 1, n 1, j 1, n .
12.Перейти к шагу 4.
13.Вывести координаты точки экстремума и значение целевой функции
вточке экстремума. Остановить алгоритм.
В рассмотренном алгоритме через центр тяжести отображалась только одна вершина хh. Существуют алгоритмы, когда через центр тяжести отображаются несколько вершин симплекса, значения целевых функций в которых больше значения целевой функции в центре тяжести. Траектория поиска экстремума по такому алгоритму представлена на рис. 3.
Метод регулярного симплекса имеет следующие недостатки:
•нет возможности ускорить спуск в удачно выбранном направлении;
•серьезные трудности обхода «седловых» точек (обход «оврагов» и «хребтов»).
Следующий пример наглядно демонстрирует идею метода регулярного симплекса.
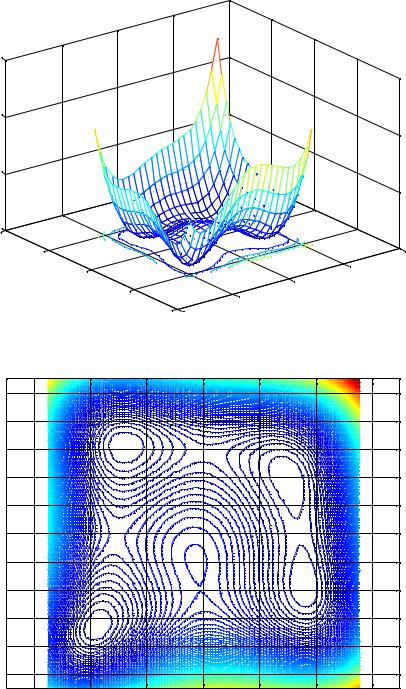
Необходимо найти оптимальные значения переменных X x1; x2 |
||||
для целевой функции |
F X x2 |
x |
11 2 x |
x2 7 2 min в окрест- |
|
1 |
2 |
1 |
2 |
ностях точки X 0 5; 5 . Целевая функция имеет несколько локальных |
||||
минимумов (рис. 1). |
Пошаговое выполнение примера позволяет просле- |
|||
3
дить перемещение частных решений, полученных на каждой итерации, к |
|||||||
локальному экстремуму. |
|
|
|
|
|
||
1500 |
|
|
|
|
|
|
|
1000 |
|
|
|
|
|
|
|
f |
|
|
|
|
|
|
|
500 |
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
10 |
|
|
|
|
|
|
|
5 |
|
|
|
|
|
10 |
|
|
0 |
|
|
|
|
5 |
|
|
|
|
|
0 |
|
|
|
|
|
-5 |
|
|
|
|
|
|
|
|
-5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
-10 |
-10 |
|
x1 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
x2 |
0 |
|
|
|
|
|
|
|
-1 |
|
|
|
|
|
|
|
-2 |
|
|
|
|
|
|
|
-3 |
|
|
|
|
|
|
|
-4 |
|
|
|
|
|
|
|
-5 |
|
|
|
|
|
|
|
-6 |
-4 |
-2 |
0 |
2 |
4 |
6 |
|
|
|
|
x1 |
|
|
|
|
Рис. 1. График и линии уровня целевой функции |
||||||
4

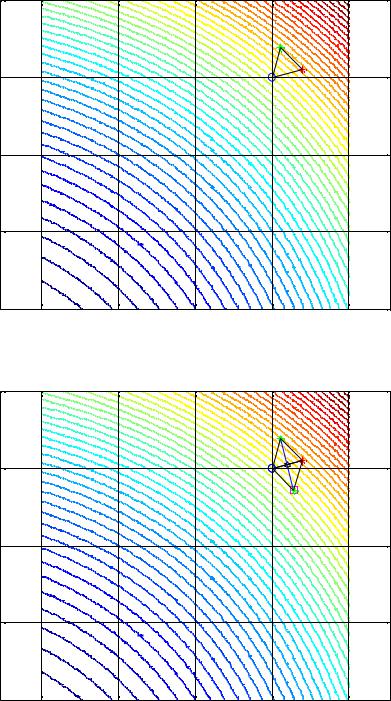
При поиске минимума целевой функции двух переменных в качестве симплекса используется равносторонний треугольник (рис. 2а). От заданной длины ребра симплекса b (т.е. длины стороны треугольника) зависит скорость поиска оптимального решения. Первоначально векторы решений X задают в вершинах симплекса, где вычисляют значения целевой функции F X . Одна из вершин исходного симплекса находится в начальной
точке X 1 X 0 5; 5 . Координаты двух других вершин исходного симплекса определяются по формулам [2]
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 1 |
|
|
|
3 2 1 |
|
||||||||||
X 2 x1 |
b |
|
|
|
|
|
|
; x1 |
b |
|
|
|
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
1 |
|
2 2 |
|
|
2 |
|
|
2 2 |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 2 1 |
|
|
|
3 1 |
||||||||||
X 3 x1 |
b |
|
|
|
|
|
|
; x1 |
b |
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
1 |
|
|
2 2 |
|
|
2 |
|
2 2 |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
Далее определяют, в какой вершине симплекса, X 1 , X 2 или X 3 целевая функция F X имеет максимальное (наихудшее) значение. Затем определяют центр тяжести симплекса (в данном случае центр равностороннего треугольника) и отражают вершину с максимальным значением целевой функции через центр тяжести.
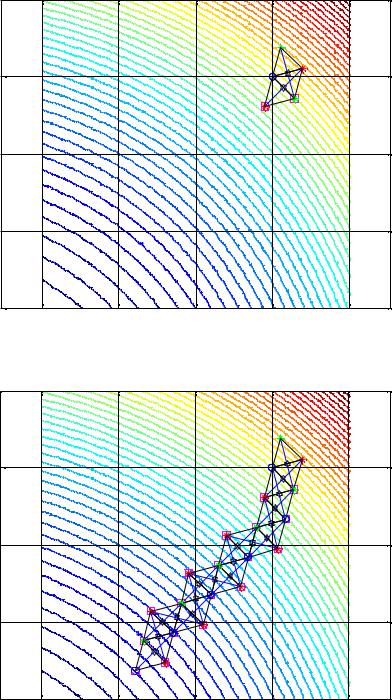
Строят новый регулярный симплекс (рис. 2б), вершинами которого будут две вершины предыдущего симплекса и отраженная вершина X 4 . В отраженной вершине вычисляют значение целевой функции F X , и процесс повторяется (рис. 2в). Таким образом, шаг за шагом регулярный симплекс перемещается в сторону минимума (рис. 2г). Дополнительно предусмотрены правила уменьшения размера симплекса и предотвращения циклического движения вокруг точки экстремума (рис. 3а).
Критерий останова алгоритма определяется по формуле
1 F X i F X 4 |
2 |
, |
|
|
|||
|
3 |
|
|
3 i 1 |
|
|
|
где – заданное малое число (в данном примере 10 4 ).
5
|
5.5 |
|
|
|
|
|
5 |
|
|
|
|
x2 |
4.5 |
|
|
|
|
|
4 |
|
|
|
|
|
3.5 |
|
|
|
|
|
3.5 |
4 |
4.5 |
5 |
5.5 |
a) |
|
|
x1 |
|
|
|
|
|
|
|
|
|
5.5 |
|
|
|
|
|
5 |
|
|
|
|
x2 |
4.5 |
|
|
|
|
|
4 |
|
|
|
|
|
3.5 |
|
|
|
|
|
3.5 |
4 |
4.5 |
5 |
5.5 |
б) |
|
|
x1 |
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
5.5 |
|
|
|
|
|
5 |
|
|
|
|
x2 |
4.5 |
|
|
|
|
|
4 |
|
|
|
|
|
3.5 |
|
|
|
|
|
3.5 |
4 |
4.5 |
5 |
5.5 |
в) |
|
|
x1 |
|
|
|
|
|
|
|
|
|
5.5 |
|
|
|
|
|
5 |
|
|
|
|
x2 |
4.5 |
|
|
|
|
|
4 |
|
|
|
|
|
3.5 |
|
|
|
|
|
3.5 |
4 |
4.5 |
5 |
5.5 |
г) |
|
|
x1 |
|
|
|
|
|
|
|
|
Рис. 2. Исходный симплекс и его отражения при пошаговом поиске экс- |
|||||
|
|
|
тремума |
|
|
|
|
|
7 |
|
|

|
2.4 |
|
|
|
|
|
|
2.35 |
|
|
|
|
|
|
2.3 |
|
|
|
|
|
|
2.25 |
|
|
|
|
|
|
2.2 |
|
|
|
|
|
x2 |
2.15 |
|
|
|
|
|
|
2.1 |
|
|
|
|
|
|
2.05 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
1.95 |
|
|
|
|
|
|
1.9 |
|
|
|
|
|
|
2.7 |
2.8 |
2.9 |
3 |
3.1 |
3.2 |
а) |
|
|
|
x1 |
|
б) |
|
|
|
|
|
5.5 |
|
|
|
|
|
|
5 |
|
|
|
|
|
|
4.5 |
|
|
|
|
|
|
4 |
|
|
|
|
|
|
3.5 |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
x2 |
|
|
|
|
|
|
2.5 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
1.5 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
0.5 |
|
|
|
|
|
|
0 |
0 |
1 |
2 |
3 |
4 |
5 |
|
|
|
|
x1 |
|
|
Рис. 3. Сжатие симплекса и траектория поиска локального минимума целе-
вой функции
8

|
|
За 49 итераций алгоритм позволяет с заданной точностью опреде- |
||||||||||
лить оптимальное решение: xопт |
3,0084 , xопт |
2,0008 |
(рис. 3б). Мини- |
|||||||||
|
|
|
|
|
|
1 |
2 |
|
X опт |
0,0028. Точное |
||
мальное значение целевой функции составляет F |
||||||||||||
|
|
|
|
|
|
|
|
min |
|
|
|
|
решение задачи (локальный минимум) находится в точке X опт 3; 2 , |
||||||||||||
F |
|
X опт |
0 . |
|
|
|
|
|
|
|
|
|
min |
|
|
|
|
|
|
|
|
|
|
|
|
|
Найти |
оптимальные |
значения x x1; x2 |
|
для целевой |
|
функции |
|||||
F |
x x2 |
x |
2 |
11 2 x |
x2 7 2 |
min в окрестностях точки x |
0 |
5; 5 . |
||||
|
|
1 |
|
1 |
2 |
|
|
|
|
|
||
%Демонстрация метода регулярного многогранника
%(симплекс-метод)
clc; close all
% График ЦФ
xi1 = -5.5:0.1:5.5; xi2 = -5.5:0.1:5.5;
[X1, X2] = meshgrid(xi1,xi2);
Fun = (X1.^2 + X2 - 11).^2 + (X1 + X2.^2 - 7).^2; figure
meshc(X1, X2, Fun); grid on figure
contour(X1, X2, Fun, 120); grid on
%линии уровня вблизи x1 = [5; 5] xi1 = 3.5:0.02:5.5;
xi2 = 3.5:0.02:5.5;
[X1, X2] = meshgrid(xi1,xi2);
Fun = (X1.^2 + X2 - 11).^2 + (X1 + X2.^2 - 7).^2; figure
contour(X1, X2, Fun, 50); hold on; axis equal
%встроенная ЦФ
F = inline('(x(1).^2+x(2)-11).^2 + (x(1)+x(2).^2- 7).^2');
n = 2; % размерность задачи
b = 0.2; % длина ребра симплекса alpha = 1; % коэффициент отображения
9

MaxNumIter = 100; % максимальное количество итераций
x1 = [5; -5]; % стартовая точка
TolFun = 0.000001;
% строим исходный симплекс
x2 = zeros(2,1); % координаты второй точки симплекса x2(1) = x1(1) + (sqrt(n+1)-1) / (n*sqrt(2)) * b; x2(2) = x1(2) + (sqrt(n+1)+n-1) / (n*sqrt(2)) * b;
x3 = zeros(2,1); % координаты третьей точки симплекса x3(1) = x1(1) + (sqrt(n+1)+n-1) / (n*sqrt(2)) * b; x3(2) = x1(2) + (sqrt(n+1)-1) / (n*sqrt(2)) * b;
x = zeros(2,3);
% записываем в массив 2*3 координаты симплекса x(:,1) = x1;
x(:,2) = x2; x(:,3) = x3;
for i=1:MaxNumIter, % цикл по номеру sprintf('Симплекс № %d', i) plot(x1(1), x1(2), 'bo'); hold on; plot(x2(1), x2(2), 'g*'); hold on; plot(x3(1), x3(2), 'r*'); grid on;
patch([x1(1) x2(1) x3(1)], [x1(2) x2(2) x3(2)], ...
[1 1 1], 'FaceColor', 'none')
F1 = F(x1);
F2 = F(x2);
F3 = F(x3);
sprintf('ЦФ в точке х1 %f', F1) sprintf('ЦФ в точке х2 %f', F2) sprintf('ЦФ в точке х3 %f', F3)
% самая высокая точка F
Fmax = max([F1 F2 F3]); switch Fmax
case F1
xh = x1; nh = 1; case F2
xh = x2; nh = 2; case F3
10
