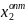Лаб. работа №4
.docxНелдер и Мид усовершенствовали метод регулярного симплекса, сохранив его достоинства, и предложили методику ускорения поиска в удачно выбранном направлении. В методе деформированного многогранника (метод Нелдера Мида) также строят исходный регулярный симплекс, определяют значения целевой функции в вершинах симплекса.
При работе с алгоритмом метода деформируемого многогранника используются следующие соглашения:
первый индекс координаты входного параметра определяет порядковый номер вершины симплекса. Количество вершин симплекса равно n+1;
второй индекс координаты входного параметра обозначает порядковый номер оси координат (координата направления). Для целевой функции двух переменных максимальное значение второго индекса j=2.
В двухмерный массив координат вершин симплекса (n+1 вершина) добавлены координаты:
n + 2 – центра тяжести;
n + З – отображенной вершины;
n + 4 – растянутой вершины;
n + 5 – сжатой вершины.
Для удобства обозначений в выражениях используются индексы: h – номер вершины симплекса, которой принадлежит максимальное значение целевой функции
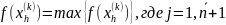
l – номер вершины симплекса, которой принадлежит минимальное значение целевой функции
k – номер шага (итерации) алгоритма.
Для определения координат центра тяжести симплекса используют выражение:
Исходный симплекс регулярный, следовательно, в начало координат можно поместить либо одну из вершин симплекса, либо центр тяжести. Из аналитической геометрии известно, что координаты вершин правильной (регулярной) фигуры можно задать с помощью матрицы
Количество столбцов матрицы D соответствует количеству вершин симплекса (n+1), а строки матрицы D содержат координаты вершин симплекса. Количество строк равно n.
Значения элементов матрицы D вычисляют по формулам:
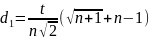
где t— расстояние между вершинами симплекса. Для большинства задач t=1.
Над отображаемой вершиной в методе деформируемого многогранника могут быть выполнены следующие процедуры.
1. Отображение вершины.
2. В случае поиска минимума целевой функции через центр тяжести отображается вершина h с наибольшим значением целевой функции.
В случае поиска максимума целевой функции – вершина l. Отображение вершины симплекса выполняется с использованием выражения:
где α > 0 коэффициент отображения
Если значение целевой функции в
отображенной вершине (n+3)
меньше, чем в вершине
,
и больше, чем в вершине
,
то координаты вершины
заменяют на координаты отображенной
вершины.
3. Растяжение вершины.
4. Если после отображения вершины симплекса оказалось, что значение целевой функции в отображаемой вершине меньше, чем во всех остальных вершинах или равно значению целевой функции в вершине , то выбранное направление удачное, т.е. где-то в этом направлении находится экстремум. Поэтому отображаемую вершину надо продвинуть в направлении отображения.
где γ > 0 коэффициент отображения
5. Если значение целевой функции в растянутой вершине меньше, чем значение целевой функции в отображенной вершине, то координаты вершины заменяются на координаты растянутой вершины. В противном случае координаты вершины заменяются на координаты растянутой вершины.
6. Сжатие вершины. Если после отображения вершины симплекса оказалось, что значение целевой функции в отображенной вершине больше или равно значению целевой функции в вершине , то направление отображения выбрано неудачно и отображенную вершину надо приблизить к центру тяжести. Сжатие вершины выполняется по формуле:
где 0 < β < 1 коэффициент отображения
Если после выполнения процедуры сжатия значение целевой функции в сжатой вершине будет меньше, чем в вершине , то выполняем замену координат вершины , на координаты сжатой вершины. В противном случае выполняется процедура редукции вершин симплекса.
По формуле (1) симплекс сжимается к вершине . Можно преобразовать формулу (1) и симплекс будет сжиматься к центру тяжести.
4. Редукция вершин. Если в результате выполнения процедур отображения и сжатия оказалось, что выполнить замену координат вершины , нельзя, то выполняется процедура редукции вершин симплекса, в результате чего геометрические размеры симплекса уменьшаются, как правило, в 2 раза. Редукция вершин симплекса выполняется по формуле:
Процедура редукции выполняется в том случае, когда нет возможности отобразить вершину , т.е. симплекс находится в окрестности экстремума и надо уточнить координаты экстремальной точки.
Для всех процедур — отображение, растяжение, сжатие, редукция и определение координат центра тяжести – вычисления по указанным формулам надо выполнить для каждого индекса (для каждого координатного направления). При выполнении процедур растяжения и сжатия исходный регулярный симплекс изменяет свои геометрические размеры и теряет свойство регулярности.
5. Критерий окончания поиска.
Критериев окончания поиска можно указать несколько. Наилучшего критерия окончания поиска нет. Авторы метода деформируемого многогранника рекомендуют в качестве критерия окончания поиска использовать выражение:
где ε – произвольное малое число, которое определяет точность вычисления значения целевой функции.
Используемый деформируемый многогранник (симплекс) наиболее удачно приспособлен к топографии целевой функции, т. е. изменяет свою форму в зависимости от «рельефа» целевой функции.
Авторы метода деформируемого многогранника провели ряд исследований и рекомендуют следующие значения коэффициентов: α=1; β=0,5 и γ=2. Другие исследователи этого метода рекомендуют α=1; 0,4 ≤ β ≤ 0,6 и 2,8 ≤ γ ≤ 3,0. Предложенные рекомендации хорошо себя показали на многих целевых функциях, хотя при исследовании специальных целевых функций значения коэффициентов могут быть другими.
Необходимо найти оптимальные значения
переменных
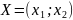для целевой функции
в окрестностях точек
методом деформируемого многогранника.
Целевая функция имеет несколько локальных
минимумов (рис. 1 и рис. 2). 
Рис. 1. График целевой функции
Р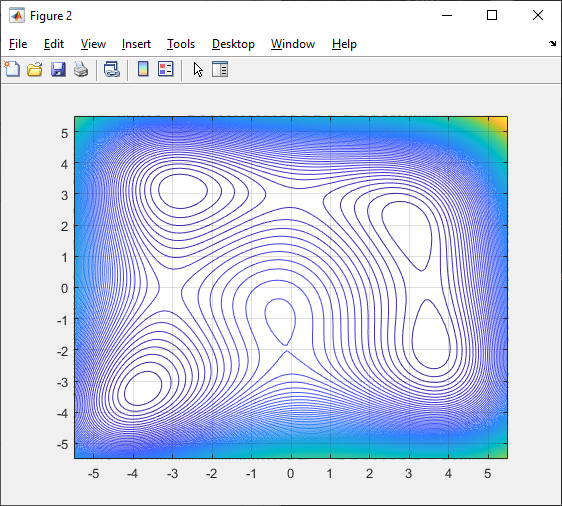
ис.
2. Линии уровня целевой функции
Пошаговое выполнение примера позволяет проследить перемещение частных решений, полученных на каждой итерации, к локальному экстремуму.
П
ри
поиске минимума целевой функции двух
переменных в качестве симплекса
используется равносторонний треугольник
(рис. 3).
Рис.3. Исходный сиплекс
От заданной длины ребра симплекса b
(т.е. длины стороны треугольника) зависит
скорость поиска оптимального решения.
Первоначально векторы решений X
задают в вершинах симплекса, где
вычисляют значения целевой функции
F(X).
Одна из вершин исходного симплекса
находится в начальной точке
.
Координаты двух других вершин исходного
симплекса определяются по следующим
формулам.
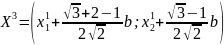
Далее определяют, в какой вершине
симплекса
или
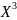целевая функция F(X)
имеет максимальное (наихудшее) значение.
Затем определяют центр тяжести симплекса
(в данном случае центр равностороннего
треугольника) и отражают вершину с
максимальным значением целевой функции
через центр тяжести.
С
троят
новый регулярный симплекс (рис. 4),
вершинами которого будут две вершины
предыдущего симплекса и отраженная
вершина
Рис. 4. Новый регулярный симплекс
Критерий остановки алгоритма определяется по формуле:
Таблица 1.
Результаты выполнения программы
|
|
|
|
(5; 5) |
3,8769 |
-2,1035 |
5.4072 |
ИСХОДНЫЙ КОД ПРОГРАММЫ
clc;
close all
% График ЦФ
xi1 = -5.5:0.1:5.5;
xi2 = -5.5:0.1:5.5;
[X1, X2] = meshgrid(xi1,xi2);
Fun = (X1.^2 + X2 - 11).^2 + (X1 + X2.^2 - 7).^2;
figure
meshc(X1, X2, Fun); grid on
figure
contour(X1, X2, Fun, 120); grid on
% линии уровня вблизи x1 = [5; 5]
xi1 = 3.5:0.02:5.5;
xi2 = 3.5:0.02:5.5;
[X1, X2] = meshgrid(xi1,xi2);
Fun = (X1.^2 + X2 - 11).^2 + (X1 + X2.^2 - 7).^2;
figure
contour(X1, X2, Fun, 50); hold on;
axis equal
% встроенная ЦФ
F = inline('(x(1).^2 + x(2) - 11).^2 + (x(1) + x(2).^2 -7).^2');
n = 2; % размерность задачи
b = 0.2; % длина ребра симплекса
alpha = 1; % коэффициент отображения
gamma = 2; % коэффициент растяжения
beta = 0.5; % коэффициент сжатия
MaxNumIter = 100; % максимальное количество итераций
x1 = [5; 5]; % стартовая точка
TolFun = 0.0001;
% строим исходный регулярный симплекс
x2 = zeros(2,1); % координаты второй точки симплекса
x2(1)=x1(1)+(sqrt(n+1)-1)/(n*sqrt(2))*b;
x2(2)=x1(2)+(sqrt(n+1)+n-1)/(n*sqrt(2))*b;
x3 = zeros(2,1); % координаты третьей точки симплекса
x3(1)=x1(1)+(sqrt(n+1)+n-1)/(n*sqrt(2))*b;
x3(2)=x1(2)+(sqrt(n+1)-1)/(n*sqrt(2))*b;
x = zeros(2,3);
% записываем в массив 2*3 координаты симплекса
x(:,1) = x1;
x(:,2) = x2;
x(:,3) = x3;
for i=1:MaxNumIter % цикл по номеру
sprintf('Симплекс № %d', i)
patch([x1(1) x2(1) x3(1)], [x1(2) x2(2) x3(2)], [1 1 1], 'FaceColor', 'none')
F1 = F(x1);
F2 = F(x2);
F3 = F(x3);
sprintf('ЦФ в точке х1 %f', F1)
sprintf('ЦФ в точке х2 %f', F2)
sprintf('ЦФ в точке х3 %f', F3)
% самая высокая точка F
Fmax = max([F1 F2 F3]);
switch Fmax
case F1
xh = x1; nh = 1;
case F2
xh = x2; nh = 2;
case F3
xh = x3; nh = 3;
end
% самая низкая точка F
Fmin = min([F1 F2 F3]);
switch Fmin
case F1
xl = x1;
case F2
xl = x2;
case F3
xl = x3;
end
% Центр тяжести, спроецированный на ребро симплекса, относительно которого выполняется отображение
x4 = 1./n.*(x1+x2+x3-xh);
plot(x4(1),x4(2),'kh');
F4 = F(x4);
% проверка критерия достаточной малости симплекса
if (((F1-F4)^2+(F2-F4)^2+(F3-F4)^2)/3 < TolFun)
disp('Сходимость достигнута');
sprintf('x1 опт = %f, x2 опт = %f, Fmin = %f', xl(1), xl(2), Fmin)
break;
end
% отображаем точку
x5 = x4 + alpha*(x4-xh);
plot(x5(1), x5(2), 'ms');
F5 = F(x5);
sprintf('ЦФ в точке х5 %f', F(x5))
if (F5 < F(xh)) % в новой точке получено меньшее значение ЦФ
x(:,nh) = x5;
plot([xh(1) x5(1)], [xh(2) x5(2)], '--')
% растяжение вершины
x6 = x4 + gamma*(x4-xh);
plot (x6(1), x6(2), 'с^');
F6 = F(x6);
plot([xh(1) x6(1)], [xh(2) x6(2)], '--')
if (F6 < F5) % в новой точке получено меньшее значение ЦФ
x(:,nh) = x6;
else % сжатие вершины
x7=x4+beta*(x4-xh);
plot(x7(1), x7(2), 'cv');
F7 = F(x7);
if (F7 < F5) % в новой точке получено меньшее значен ЦФ
x(:,nh) = x7;
end
end
else % сжатие симплекса
if(x1~=xl), x(:,1)=xl+0.5*(x1-xl); end
if(x2~=xl), x(:,2)=xl+0.5*(x2-xl); end
if(x3~=xl), x(:,3)=xl+0.5*(x3-xl); end
end
x1 = x(:,1);
x2 = x(:,2);
x3 = x(:,3);
end