Лаб. работа №3

При решении задачи оптимизации вида , , в которых целевая функция нелинейна и ограничения отсутствуют, могут применяться методы прямого поиска, градиентные методы (первого порядка) и второго порядка. Методы прямого поиска – это методы, вычисляющие и минимизирующие F(X) без ее дифференцирования (программная функция fminsearch в MATLAB Optimization Toolbox). Методы первого и второго порядка используют информацию о градиенте целевой функции или о производных второго порядка (надстройка «Поиск решения» MS Office Excel или программная функция fminunc в MATLAB Optimization Toolbox). Методы прямого поиска обладают хорошей устойчивостью и позволяют исследовать недифференцируемые функции. Методы на основе вычисления производных позволяют повысить скорость поиска оптимума, но накладывают ряд условий на вид целевой функции.

МЕТОД РЕГУЛЯРНОГО СИМПЛЕКСА

Метод поиска экстремума с помощью регулярного симплекса получил свое название за счет использования регулярной (равносторонней) фигуры в n-мерном пространстве Регулярный многогранник называется симплексом. Для вектора переменных , симплекс в n-мерном пространстве описывается n+1 вершинами. В двумерном пространстве проектирования симплекс представляет собой равносторонний треугольник, в трехмерном – тетраэдр.

На каждом шаге поиска рассчитывается новая точка решения внутри или вблизи симплекса. Значение функции в новой точке сравнивается со значениями функции в вершинах симплекса, и, как правило, одна из вершин заменяется новой точкой, образуя новый симплекс. Процедура повторяется до тех пор, пока размер симплекса не станет меньше заданной погрешности вычислений. По сравнению с градиентными методами, в ряде случаев симплекс-метод является более устойчивым.

При поиске минимума целевой функции f(x) двух переменных в качестве симплекса используется равносторонний треугольник. Первоначально векторы входных параметров задают в вершинах симплекса, где и вычисляют значения целевой функции. далее определяют, в какой вершине симплекса целевая функция имеет максимальное значение. Затем определяют центр тяжести симплекса (в данном случае центр равностороннего треугольника) и отображают вершину с максимальным значением целевой функции через центр тяжести (рис. 2).

Строят новый регулярный симплекс, вершинами которого будут две вершины предыдущего симплекса и отображенная вершина. В отображенной вершине вычисляют значение целевой функции, и процесс повторяется. Таким образом, шаг за шагом регулярный симплекс перемещается в сторону минимума. дополнительно предусмотрены правила уменьшения размера симплекса и предотвращения циклического движения вокруг точки экстремума.

Исходный симплекс имеет вершины а, b и с. В вершине а значение целевой функции имеет максимальное значение. Вершина а через центр тяжести отображается, и таким образом, получена отображенная вершина d. Отображенный симплекс имеет вершины b, с и d (рис. 2). Поиск экстремума заключается в последовательном отображении вершины симплекса и его сжатии (уменьшении размера симплекса). Траектория поиска экстремума целевой функции показана на рис. 3. для уточнения точки экстремума на последнем шаге надо выполнить сжатие симплекса

АЛГОРИТМ МЕТОДА РЕГУЛЯРНОГО СИМПЛЕКСА

1. Задать координаты и стартовой (базовой) точки. Для n-мерного случая — n координат.

2. Задать длину ребра (b) регулярного симплекса.

3. Вычислить координаты вершин симплекса по формулам:

4. В каждой вершине симплекса определить значение целевой функции L(х).

5. Вычислить критерий останова алгоритма по формуле:

Если критерий останова алгоритма меньше , то перейти к шагу 13. Если «нет», то перейти к шагу 6.

6. Определить вершину с максимальным значением целевой функции и присвоить ей индекс h, т.е. L(хh) Определить вершину с минимальным значением целевой функции и присвоить ей индекс l, т.е. L(хl).

7. Вычислить координаты центра тяжести (порядковый номер вершины п + 2) по формуле:

8. Отобразить вершину хh через центр тяжести, т. е. пересчитать координаты вершины (порядковый номер отображенной вершины п + 3) по формуле:

9. Вычислить значение целевой функции в отображенной вершине.

10. Если значение целевой функции в отображенной вершине меньше, чем в вершине хh, то заменить вершину хh симплекса на отображенную вершину. Если «нет», то перейти к шагу 11.

11. Выполнить редукцию (сжатие к вершине хl симплекса) симплекса по формуле:

12. Перейти к шагу 4.

13. Вывести координаты точки экстремума и значение целевой функции в точке экстремума. Остановить алгоритм.

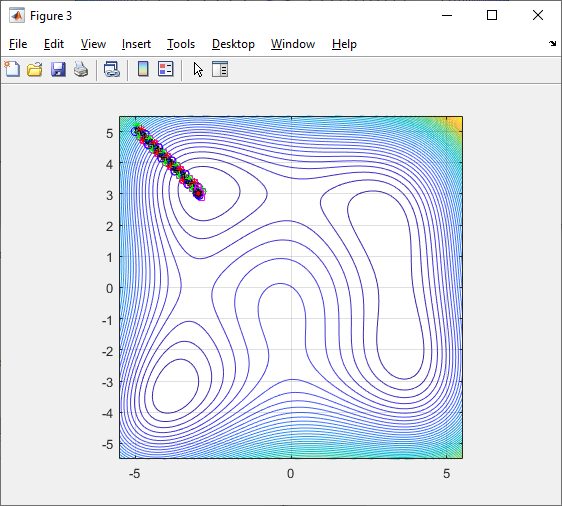
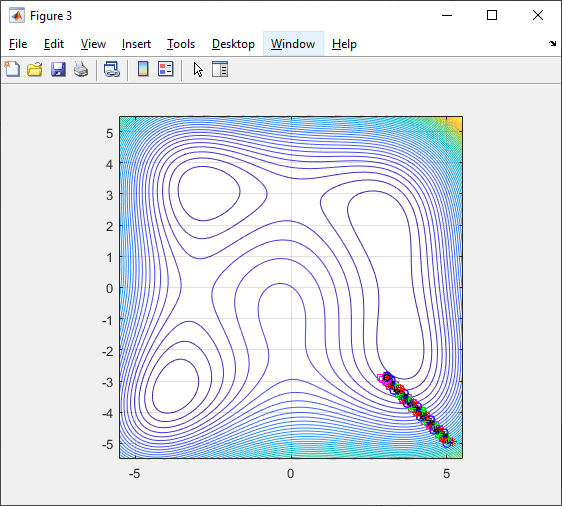
Необходимо найти оптимальные значения переменных для целевой функции в окрестностях точек ; ; ; . Целевая функция имеет несколько локальных минимумов (рис. 1 и рис. 2).

Рис. 1. График целевой функции

Р ис. 2. Линии уровня целевой функции

Пошаговое выполнение примера позволяет проследить перемещение частных решений, полученных на каждой итерации, к локальному экстремуму.

П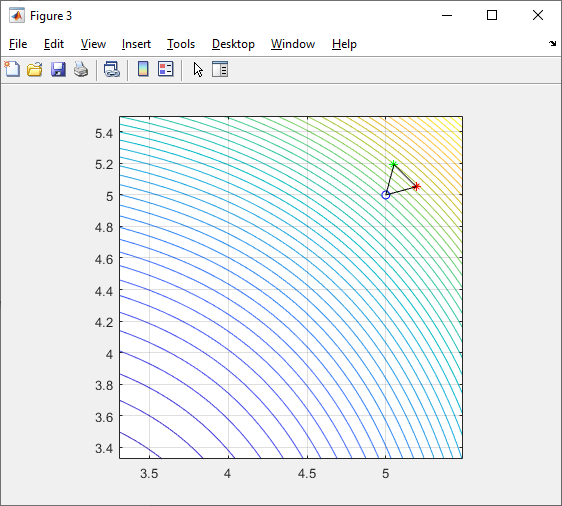 ри поиске минимума целевой функции двух переменных в качестве симплекса используется равносторонний треугольник (рис. 3).

Рис.3. Исходный сиплекс

От заданной длины ребра симплекса b (т.е. длины стороны треугольника) зависит скорость поиска оптимального решения. Первоначально векторы решений X задают в вершинах симплекса, где вычисляют значения целевой функции F(X). Одна из вершин исходного симплекса находится в начальной точке . Координаты двух других вершин исходного симплекса определяются по следующим формулам.

Далее определяют, в какой вершине симплекса или целевая функция F(X) имеет максимальное (наихудшее) значение. Затем определяют центр тяжести симплекса (в данном случае центр равностороннего треугольника) и отражают вершину с максимальным значением целевой функции через центр тяжести.

С троят новый регулярный симплекс (рис. 4), вершинами которого будут две вершины предыдущего симплекса и отраженная вершина .

Рис. 4. Новый регулярный симплекс

В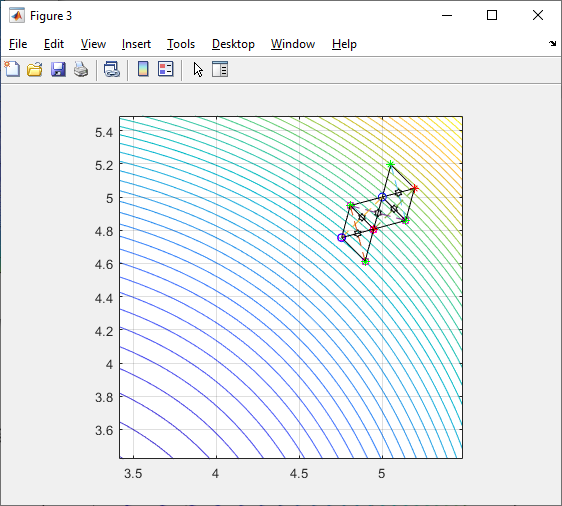 отраженной вершине вычисляют значение целевой функции F(X), и процесс повторяется (рис. 5).

Рис. 5. Повторение процесса вычисления значения целевой функции

Т аким образом, шаг за шагом регулярный симплекс перемещается в сторону минимума (рис. 6).

Рис. 6. Отражение исходного симплекса при пошаговом поиске экстремума

Критерий остановки алгоритма определяется по формуле:

Таблица1.

	Траектория поиска локального минимума целевой функции
(5; 5)
(-5; 5)
(5; -5)
(-5; -5)

Таблица 2.

Результаты выполнения программы

(5; 5)	2,5930	2,4908	831.6953
(-5; 5)	-2,9753	3,0174	831.6953
(5; -5)	3,0782	-2,8868	831.6953
(-5; -5)	-3,4098	-3,6612	831.6953

ИСХОДНЫЙ КОД ПРОГРАММЫ

clc; close all

% график ЦФ

xi1 = -5.5:0.1:5.5;

xi2 = -5.5:0.1:5.5;

[X1, X2] = meshgrid (xi1, xi2);

Fun = (X1.^2 + X2 - 11).^2 + (X1 + X2.^2 - 7).^2;

figure

meshc (X1, X2, Fun); grid on

figure

contour (X1, X2, Fun, 120); grid on

%линии уровня вблизи х1 = [5;5]

xi1 = 3.5:0.02:5.5;

xi2 = 3.5:0.02:5.5;

[X1, X2] = meshgrid (xi1, xi2);

Fun = (X1.^2 + X2 - 11).^2 + (X1 + X2.^2 - 7).^2;

figure

contour (X1, X2, Fun, 50); hold on;

axis equal

%встроенная ЦФ

F = inline ('(x(1).^2 + x(2)-11 + x(1)+x(2).^2 - 7).^2');

n = 2; %размерность задачи

b = 0.2; % размерность симплекса

alpha = 1; %коофицент отображения

MaxNumIter = 100; %максимальное кол-во итераций

x1 = [5; -5]; %стартовая точка

TolFun = 0.000001;

%строим исходный симлекс

x2 = zeros (2,1); %координаты второй точки сиплекса

x2 (1) = x1(1) + (sqrt(n+1)-1) / (n*sqrt(2)) * b;

x2 (2) = x1(2) + (sqrt(n+1)+n-1) / (n*sqrt(2)) * b;

x3 = zeros (2,1); %координаты второй точки сиплекса

x3 (1) = x1(1) + (sqrt(n+1)+n-1) / (n*sqrt(2)) * b;

x3 (2) = x1(2) + (sqrt(n+1)-1) / (n*sqrt(2)) * b;

x = zeros(2,3);

%записываем в массив 2*3 координаты сиплекса

x(:,1) = x1;

x(:,2) = x2;

x(:,3) = x3;

for i=1 : MaxNumIter %цикл по номеру

sprintf ('Симплекс № %d', i)

plot (x1(1), x1(2), 'bo'); hold on;

plot (x2(1), x2(2), 'g*'); hold on;

plot (x3(1), x3(2), 'r*'); hold on;

patch ([x1(1) x2(1) x3(1)], [x1(2) x2(2) x3(2)], [1 1 1], 'FaceColor', 'none')

F1 = F(x1);

F2 = F(x2);

F3 = F(x3);

sprintf ('ЦФ в точке х1 %f', F1)

sprintf ('ЦФ в точке х2 %f', F2)

sprintf ('ЦФ в точке х3 %f', F3)

%самая высокая точка F

Fmax = max ([F1 F2 F3]);

switch Fmax

case F1

xh = x1; nh = 1;

case F2

xh = x2; nh = 2;

case F3

xh = x3; nh = 3;

end

%самая низкая точка F

Fmax = min ([F1 F2 F3]);

switch Fmax

case F1

xl = x1;

case F2

xl = x2;

case F3

xl = x3;

end

%Центр тяжести, спроецированный на ребро симплекса,

%относительно которого выполняется отображение

x4 = 1./n.* (x1+x2+x3-xh);

plot (x4(1), x4(2), 'kh'); hold on;

F4 = F(x4);

%проверка критерия достаточной малости симплекса

if (((F1-F4)^2+(F2-F4)^2+(F3-F4)^2)/3 < TolFun),disp('Сходимость достигнута');

sprintf('x1 опт = %f, x2 опт = %f, Fmin = %f', xl(1), xl(2), Fmin)

break;

end

%отображаем точку

x5 = x4 + alpha*(x4-xh);

plot (x5(1), x5(2), 'ms'); hold on;

plot ([xh(1), x5(1)], [xh(2), x5(2)], '--')

F5 = F(x5);

sprintf ('ЦФ в точке x5 %f', F(x5))

if (F5<F(xh)) % в новой точке получено меньшее значение ЦФ

x(:, nh) = x5;

else %сжатие симплекса

if (x1 ~= xl), x(:,1) = x1 + 0.5*(x1 - x1); end

if (x2 ~= xl), x(:,2) = x1 + 0.5*(x2 - x1); end

if (x3 ~= xl), x(:,1) = x1 + 0.5*(x3 - x1); end

end

x1 = x(:,1);

x2 = x(:,2);

x3 = x(:,3);

end