Вопрос 7. Определение вероятности перехода цепи Маркова за m шагов.

Ответ:

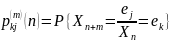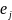Если – вероятность перехода из состояния в состояние за 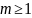шагов, то для однородной цепи Маркова имеем:

Первая задача в теории цепей Маркова состоит в определении вероятности перехода из состояния в состояние за 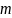шагов. Пусть – цепь Маркова с матрицей переходных вероятностей и множеством состояний . Матрица переходных вероятностей определяет вероятности перехода за 1 шаг.

Для однородной цепи Маркова с матрицей переходных вероятностей при любом справедливо равенство: .

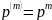Цепь Маркова называется неоднородной, если переходные вероятности зависят от номера испытания .

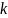В этом случае переходные вероятности обозначаются как 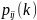. Тогда матрица переходных вероятностей будет зависеть от .

Вопрос 8. Примеры цепей Маркова.

Ответ:

Пространственно-однородные цепи Маркова. Пусть дискретная случайная величина ξ принимает неотрицательные целочисленные значения, причем 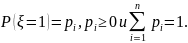Пусть ξ₁, ξ_{2, …} , ξ_n, … – результаты независимых наблюдений случайной величины ξ.

a) Определим процесс X(t), n = 0, 1, 2, …, положив X_n = ξ_n, где X₀ = ξ₀ задано.Матрица переходных вероятностей имеет вид

P = .

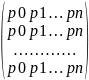У P все строки одинаковы, следовательно, случайная величина X_n+1 не зависит от случайной величины X_n.

a) Определим процесс X(t), n = 0, 1, 2, …, положив X_n = S_n, где S_n = ξ₁ + ξ_{2 + …} + ξ_n. Считаем, что S₀ = 0. Найдем матрицу переходных вероятностей.

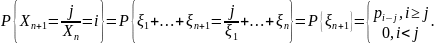
P =

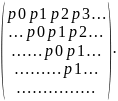
Процесс X_n образует ЦМ.

Одномерные случайные блуждания. Пусть η₁, η₂, … - независимые одинаково распределенные случайные величины. P {η_k = -1} = q, P {η_k = 1} = p, а последовательность ξ_t строится по правилу

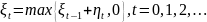
и называется случайным блужданием на множестве неотрицательных целых чисел с отражающим экраном в 0.

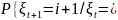i} = p,

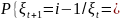i} = q = 1 - p, i≥ 1,

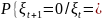0} = q.

P =

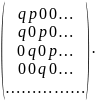
Модель Эренфестов для процесса диффузии. Эта модель представляет собой цепь с (n + 1) состояниями и возможными переходами только в состояния, соседние справа и слева. Тогда переходные вероятности определяются равенствами:

Цепь имеет две физические интерпретации. Рассмотрим модель Эренфестов. Ученые физики описали мысленный эксперимент, при котором перемещали n частиц по двум сосудам. В каждый момент времени t = 0, 1, … случайно, равновероятно и независимо от предыстории выбирается одна из n частиц и перемещается в другой сосуд. Пусть ξ_t – число частиц в первом сосуде в момент t. Состоянием процесса считается число частиц (0, 1, 2, …, n) в первом сосуде, и переходные вероятности имеют вид:

=

=

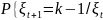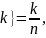
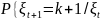Тогда

P =

Следовательно, эксперимент описывается цепью Маркова.

Вопрос 9. Классификация состояний цепи Маркова

Ответ:

Состояние 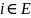называется несущественным, если найдется 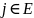, такое что 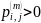для некоторого , но 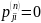для всех . В противном случае состояние называется существенным.

Состояние называется поглощающим, если .

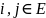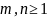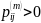Состояния называются сообщающимися, если найдутся такие , что и 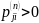. Сообщающиеся состояния всегда существенны.

Цепь Маркова, состоящая из одного класса сообщающихся состояний, называется неразложимой. Если она содержит более одного класса сообщающихся состояний, то она разложима.

Пусть 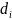– НОД чисел 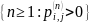. Состояние называется периодическим с периодом , если 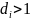. В противном случае состояние – апериодическое.

Если 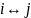, то .

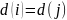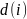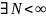Если состояние имеет период , то и 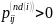для всех .

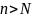Существенное состояние называется возвратно нулевым, если 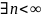такое что 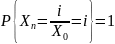, и невозвратным если .

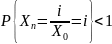Существенное состояние называется возвратно нулевым, если , при .

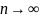Неразложимая цепь Маркова называется апериодической, если все ее состояния апериодические.

Существенное состояние называется возвратным, если такое что 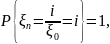и невозвратимым, если .

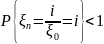Существенное состояние называется возвратным нулевым, есл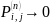и при .

Неразложимая цепь Маркова называется апериодической, если все её состояния апериодические

Для неразложимой цепи Маркова справедливы свойства:

а) если хотя бы одно состояние возвратно, то и все другие возвратны;

б) если хотя бы одно состояние нулевое, то все другие состояния возвратно нулевые;

в) если хотя бы одно состояние имеет период d>1, то и все остальные периодичны с периодом d.

Таким образом, неразложимая цепь Маркова будет апериодической, если хотя бы одно из её состояний – апериодическое.