Вопрос 3. Классификация случайных процессов. Марковские процессы. Стационарные случайные процессы.
Ответ:
Основные признаки, по которым различаются случайные процессы касаются природы пространства состояний обозначаемого через E временного параметра T и отношений зависимости между случайными величинами. В качестве классических типов случайных процессов можно выделить:
1. Мартингалы
2. Процесс с независимыми приращениями
3. Марковские процессы
Являются самым крупным направлением в теории случайных процессов.
Определение.
Случайный
процесс
называется марковским, если выполняется
условие Маркова: для любых упорядоченных
моментов времени
справедливо соотношение:
Где
.
Таким образом, будущее состояние системы зависит от прошлого только через настоящее. Марковские процессы являются естественным обобщением детерминированных процессов, рассматриваемых в классической физике. Любые случайные блуждания по целым числам – числовой линии и проблемы разорения игрока представляют собой классические примеры марковских процессов с дискретным временем. Двумя важными примерами марковских процессов с непрерывным временем являются винеровский процесс, известный как процесс броуновского движения, и процесс Пуассона. Марковские процессы получили широкое применение в качестве статистических моделей реальных явлений – в теории массового обслуживания. Известный алгоритм PageRank, который первоначально был предложен для поисковой системы Google, основан на марковском процессе.
4. Стационарные случайные процессы
Определение.
Случайный
процесс
называется стационарным в узком смысле,
если совместные распределения семейств
и
одинаковы при всех
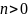и всех
,
т.е.
-мерная
функция распределения инвариантна
относительно сдвига во времени.
Определение.
Случайный
процесс
называется стационарным в широком
смысле, если его математическое ожидание
и дисперсия не зависят от времени, а
ковариационная функция зависит только
от разности своих аргументов, т.е.
где
Узкое и широкое определение стационарности не тождественны. Случайные процессы, стационарные в узком смысле, всегда стационарны в широком смысле, но не наоборот.
Схема стационарных случайных процессов с хорошим приближением описывает многие реальные явления, сопровождающиеся неупорядоченными флуктуациями. Так, например, пульсации силы тока или напряжения в электрической цепи можно рассматривать как стационарный случайный процесс, если эта цепь находится в стационарном режиме, т.е. если все ее макроскопические характеристики и все условия, вызывающие протекание через нее тока, не меняются во времени.
Вопрос 4. Классификация марковских случайных процессов.
Ответ:
Марковские процессы различаются состояниями во времени и в пространстве. В отношении состояния процесса во времени различают два типа марковских процессов: с дискретным временем и непрерывным временем.
Марковским случайным процессом с дискретным временем называется такой процесс, у которого переходы из одного состояния в другое возможны в строго определенные, заранее заданные моменты времени t1, t2, …, tk, называемые шагами процесса. Такой процесс называется цепью Маркова или процессом с дискретным параметром T, который может быть процессом с конечным или бесконечным множеством состояний.
Марковским случайным процессом с непрерывным временем называется такой процесс, у которого переход из одного состояния в другое возможен в любой момент времени t.
Случайные процессы, в том числе марковские, могут быть с дискретным числом состояний. В этом случае они называются дискретными случайными процессами. Число состояний является счетным конечным или бесконечным. И выделяют класс непрерывных случайных процессов, для которых возможно бесконечное множество состояний.
Цепь Маркова: T – дискретно, E – дискретно; дискретный марковский процесс: T – непрерывно, E – дискретно; марковская последовательность: T – дискретно, E – непрерывно; непрерывный марковский процесс: T – непрерывно, E – непрерывно.