Вопрос 27. Тождество Вальда. Доказательство тождества Вальда по Колмогорову-Прохорову.
Ответ:
Тождество
Вальда.
Пусть
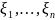– независимые случайные величины и
.
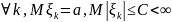Положим
.
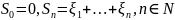Пусть
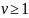– момент остановки относительно потока
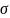– алгебр
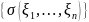и
.
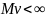Тогда
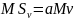
Доказательство данного тождества по Колмогорову-Прохорову.
Положим
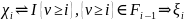и
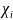независимы
.
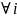Покажем, что ряд
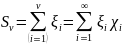
Сходится абсолютно.
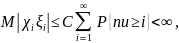
Т.к. сумму последнего ряда, мы уже считали. Вследствие абсолютной сходимости ряд можно почленно проинтегрировать, получив:
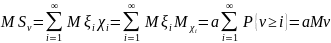
Что и требовалось доказать.
Вопрос 28. Применение тождества Вальда для случайного блуждания.
Ответ:
Рассмотрим одномерные блуждания, когда случайные приращения координаты распределены по нормальному закону со средним значением μ и дисперсией σ2, т.е.
f*(ω) = exp (-μω - σ2ω/2).
В этом случае ω0 = 2μ/ σ2 и для вероятности поглощения pc и pd следуют приближенные соотношения
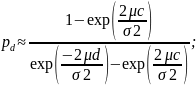
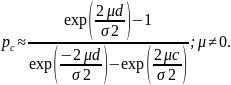
Для среднего числа шагов до поглощения получим
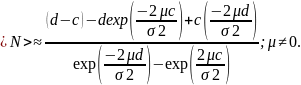
Вопрос 29. Теорема Дуба о преобразовании свободного выбора.
Ответ:
Определение
1. Пусть
– момент остановки. Для всякого
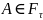определим функцию
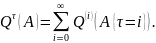Ясно, что
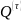– неотрицательная
– конечная мера на
.
Если момент остановки
ограничен, то мера
ограничена.
Определение
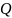2. Пусть
есть
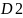с равномерно ограниченными плотностям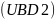и
и
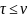– такие два момента остановки, что
.
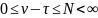Пусть
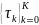– последовательность
МО, удовлетворяющая условиям
Для
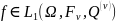определим оператор
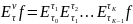
Теорема Дуба. Если есть UDB1 и , то справедлива формула
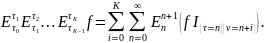
из данной теормы легко вытекает корректность предыдущего определения.
Теорема 2 (обобщение теоремы Дуба на деформированные субмартингалы).
Если
есть UDB2,
процесс
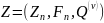есть DSubM,
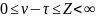и
.
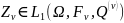То справедливо неравенство
– п.в.
Можно
показать, что если в теореме 2 МО
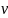ограничен, то эта теорема верна, когда
есть BD2 (включение
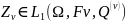выполняется в данном случае автоматически).
Вопрос 30. Неравенство Дуба для максимального значения мартингала.
Ответ:
Пусть (Ω, F, P) – вероятностное пространство, (F1 ⊂F2 ⊂ … ⊂ Fn ⊂ F) – неубывающее семейство σ-подалгебр F. Последовательность X – (ξn, Fn), n-1, …, N, называется мартингалом, если
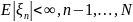
и
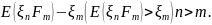
Теорема (Неравенство Дуба для максимума). Пусть X – (ξt, Ft), n-1, …, N, неотрицательный субмартингал. Пусть EξNP <∞ (1<p <∞). Тогда
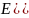
и