Вопрос 25. Понятие мартингала, субмартингала, супермартингала. Свойства мартингала, субмартингала, супермартингала.
Ответ:
Определение.
Пусть
.
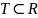Процесс (
называется мартингалом относительно
фильтрации
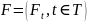если:
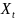согласован
с
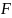.является
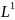– процессом, т.е.
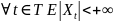
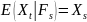п.н.
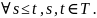
Если вместо условия 3 выполнено
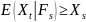п.н.
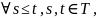
То называется субмартингалом относительно F.
Если же вместо условия 3 выполнено
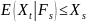п.н.
То называется супермартингалом относительно F.
Субмартингалы
и супермартингалы – это мартингалы
«наполовину». Для мартингалов условие
3 означает, что функция среднего является
постоянной
.
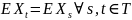Свойства мартингалов:
Случайный процесс является мартингалом тогда и только тогда, когда он является одновременно субмартингалом и супермартингалом.
Если
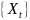– мартингал, то
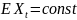.Если
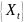– субмартингал, то
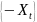– супермартингал.Если является мартингалом, а
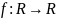– выпуклая функция, то
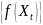– субмартингал. Если
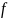вогнутая функция, то
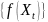– супермартингал.Вообще говоря, мартингал не является марковский процессом. Верно и обратное: марковский процесс не обязан быть мартингалом.
Вопрос 26. Разложение Дуба.
Ответ:
В теории случайных процессов в дискретном времени, являющейся частью математической теории вероятностей, теорема о разложении Дуба дает уникальное разложение каждого адаптированного и интегрируемого случайного процесса в виде суммы мартингала и предсказуемого процесса.
Пусть (Ω, F, ℙ) - вероятностное пространство, I = {0, 1, 2, . . ., N} с N ∈ ℕ или я = ℕ 0 конечное или бесконечное множество индексов, (Fn) п ∈ Я фильтрации из F, и Х = (Хn) n ∈ Я адаптированный случайный процесс с E [| Xn|] <∞ для всех n ∈ I. Тогда существует мартингал М = (Мn) n ∈ I и интегрируемый предсказуемый процесс A = (An) n ∈ I, начиная с A0 = 0, так что Хn = Мn + n для любого n ∈ I. Здесь предсказуемые означает, что n является Fn-1 - измеримы для любого n ∈ I \ {0}. Это разложение почти наверняка единственное.
Замечание. Теорема дословно справедлива также для случайных процессов X, принимающих значения в d-мерном евклидовом пространстве ℝd или комплексном векторном пространстве ℂd. Это следует из одномерного варианта при индивидуальном рассмотрении компонентов.
Доказательство.
Существование. Используя условные ожидания, определите процессы A и M для каждого n ∈ I явно как
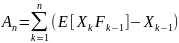
и
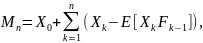
где суммы для n = 0 являются пустыми и определяется как ноль. Здесь A складывает ожидаемые приращения X, а M складывает неожиданности, т. e. ту часть каждого Xk, которая не известна на один временной шаг раньше. Из этих определений, Аn+1 (если n+1 ∈ I ) и Мn есть Рn -измеримой , потому что процесс Х приспособлен, Е [| An |] <∞ и E [| Мn |] <∞ , так как процесс X интегрируем, и разложение Xn = Мn +n справедлива для любого n ∈ I .
Уникальность.
Чтобы доказать единственность, пусть
X = M ' + A ' - дополнительное разложение.
Тогда процесс Y: = M - M ' = A ' - A является
мартингалом, из чего следует, что
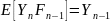так как,
а также предсказуемым, подразумевая, что
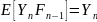так
как
для любого n ∈ I \ {0}. Поскольку Y0 = A'0 – A0 = 0 по соглашению о начальной точке предсказуемых процессов, это итеративно означает, что Yn = 0 почти наверняка для всех n ∈ I , следовательно, разложение почти наверняка единственное.