Практикум 2.3. Числовые ряды

Цель работы – усвоить базовые понятия теории числовых рядов, научиться исследовать ряды на сходимость, используя признаки сходимости, научиться использовать средства пакета MatLab для исследования рядов на сходимость и для приближенного вычисления суммы ряда.

Продолжительность работы - 4 часа.

Оборудование, приборы, инструментарий – работа выполняется в компьютерном классе с использованием пакета MatLab.

Порядок выполнения

1. Упражнения выполняются параллельно с изучением теоретического материала.

2. После выполнения каждого упражнения результаты заносятся в отчёт.

3. При выполнении упражнений в случае появления сообщения об ошибке рекомендуется сначала самостоятельно выяснить, чем оно вызвано, и исправить команду; если многократные попытки устранить ошибку не привели к успеху, то проконсультироваться с преподавателем.

4. Дома доделать упражнения из раздела «Краткие теоретические сведения и практические упражнения», которые Вы не успели выполнить во время аудиторного занятия.

5. После выполнения упражнений выполнить дополнительные упражнения для самостоятельной работы и ответить на контрольные вопросы и (см. ниже).

6. Подготовить отчёт, в который включить упражнения из раздела «Краткие теоретические сведения и практические упражнения» и упражнения для самостоятельной работы. Отчёт представить в виде документа Microsoft Word, имя файла (пример): mp_10_Ivanov_P_01_s_1 (факультет_группа_Фамилия студента_Инициал_номер лабораторной, семестр). Отчет должен содержать по каждому выполненному упражнению: № упражнения, текст упражнения; команды, скопированные из командного окна, с комментариями к ним и результаты их выполнения, включая построенные графики; тексты М-сценариев и М-функций; выводы.

Краткие теоретические сведения и практические упражнения

1. Числовой ряд. Сходящиеся и расходящиеся ряды. Сумма ряда.

Пусть задана бесконечная последовательность чисел Рассмотрим выражение, представляющее собой «сумму бесконечного множества слагаемых». Оно называетсячисловым рядом, а сами числа -членами ряда. Член ряда с произвольным номеромназываетсяобщим членом.

Например, есть ряд с общим членом, аесть ряд с общим членом.

Числа , , и т.д. называются частичными суммами ряда. Обобщая: -я частичная суммаесть сумма первыхчленов ряда: .

В качестве примера рассмотрим ряд .. Члены этого ряда,, образуют геометрическую прогрессию с первым членоми знаменателеми, значит,-я частичная суммаэтого ряда является суммой первыхчленов геометрической прогрессии и может быть найдена по формуле. Таким образом,.

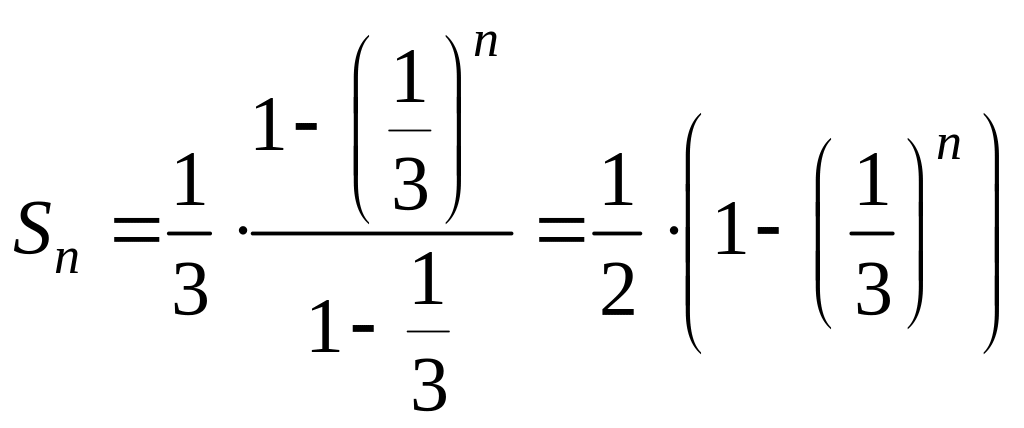Если последовательность частичных сумм ряда имеет конечный предел, т.е. существует число, то ряд называется сходящимся, а числоназывается суммой ряда. В этом случае также говорят, чторяд сходится к сумме и пишут. Если же равен бесконечности или не существует, то говорят, что рядрасходится или, что он не имеет суммы.

Продолжим рассмотрение примера. Для ряда конечный предел частичных сумм существует: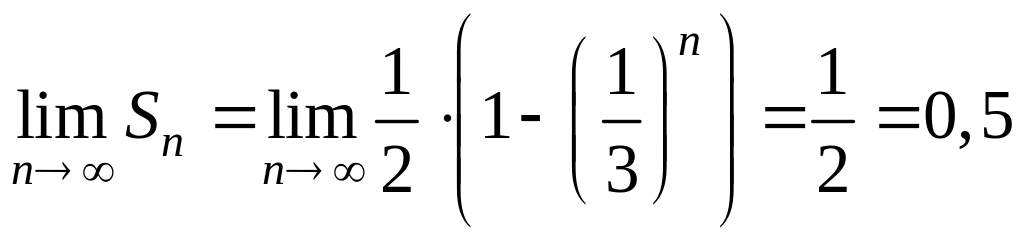. Следовательно, этот ряд сходится и его сумма равна.

Упражнение 1. Создать M-функцию, которая строит в одной системе координат график последовательности членов ряда и график последовательности частичных сумм ряда. При построении этой пары графиков использовать разные цвета и маркеры. В качестве входных параметров M-функции использовать формулу общего члена последовательности и числорассматриваемых членов. В качестве выходных параметров вывести значения. Применить созданную М-функцию для исследования следующих рядов:

1) ; 2); 3).

Опираясь на построенные графики, для каждого ряда выдвинуть гипотезу о сходимости или расходимости ряда. В случае предположения о сходимости ряда указать приблизительное значение суммы ряда.