5.3. Парабола

Определение 6. Параболой называется геометрическое место точек плоскости, для каждой из которых расстояние до некоторой фиксированной точки этой плоскости, называемой фокусом, равно расстоянию до некоторой фиксированной прямой, называемой директрисой.

Обозначим фокус параболы через , директрису – через . Тогда

параболе .

В ведем систему координат. Проведем через прямую , точку пересечения обозначим , ось направим по вектору через точки и , ось – через середину отрезка перпендикулярно оси (рис. 5.9).

Обозначим , .

Точка параболе . (5.15)

Замечание. Точек параболы нет в области .

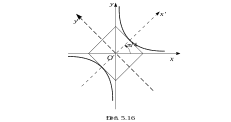
Д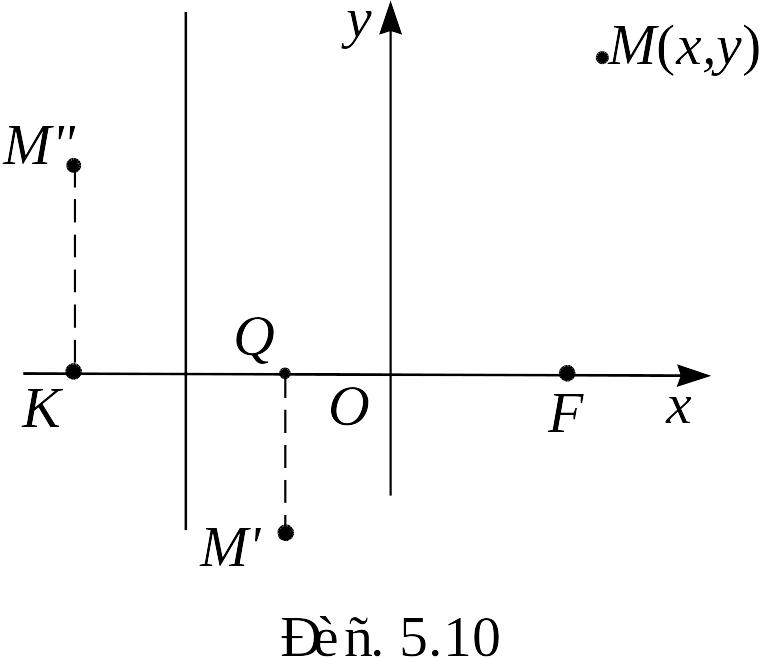 ействительно (рис. 5.10), если точка принадлежит полосе между и , то

.

Если точка лежит левее директрисы, т.е. в полуплоскости , то .

Из (5.15) получим, возведя в квадрат:

, или

. (5.16)

Пусть такова, что и удовлетворяют уравнению (5.16). Тогда

.

Следовательно, уравнение (5.16) – уравнение параболы.

Уравнение (5.16) называется каноническим уравнением параболы, - параметром параболы.

Утверждение 5. Парабола имеет ось симметрии.

В самом деле, если принадлежит параболе, то тоже принадлежит параболе (так как переменная входит в уравнение (5.16) в четной степени), - это и означает, что парабола симметрична относительно оси .

Определение 7. Ось симметрии параболы называется осью параболы, точка пересечения параболы с осью – вершиной параболы (на Рис. 5.11 – т. ).

Замечание. Фокус параболы расположен на ее оси.

И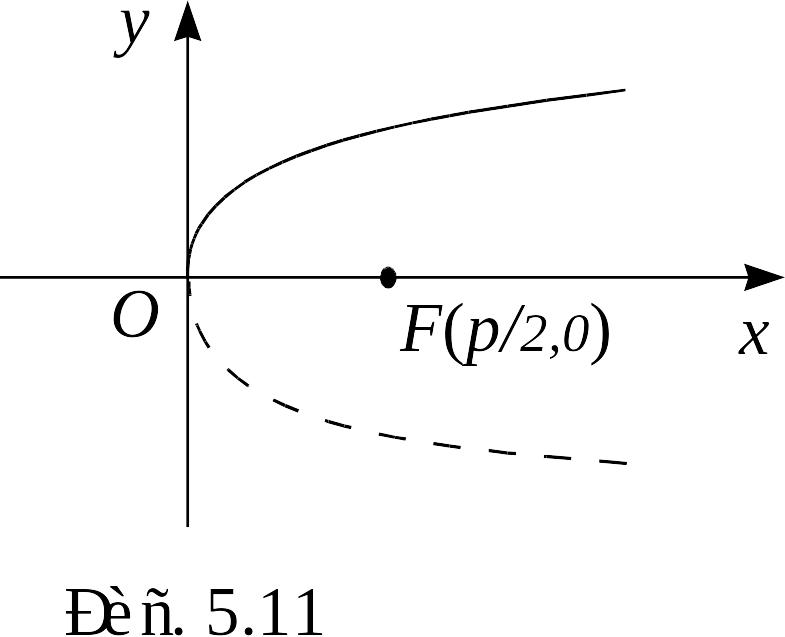 з уравнения (5.16) имеем .

Рассмотрим ветвь параболы, расположенную в I четверти, она задается уравнением .

При возрастании от до переменная возрастает от до .

«Эскиз» параболы изображен на рис. 5.11.

Замечание. Пусть - декартова система координат. Алгебраическое уравнение 2-го порядка

(5.17)

определяет относительно алгебраическую линию 2-го порядка (определение 2 в лекции 3).

В соответствии с этим эллипс, гипербола и парабола – алгебраические линии 2-го порядка. Ими не исчерпываются все частные случаи уравнения (5.17).

Пример 1. Уравнение

(5.18)

определяет пару пересекающихся прямых.

Действительно, из (5.18) получим (рис. 5.12).

Упражнение. Определить вид и расположение кривой 2-го порядка, определяемой уравнениями:

1) ; 2) .

5.4. Преобразование декартовых прямоугольных координат на плоскости

П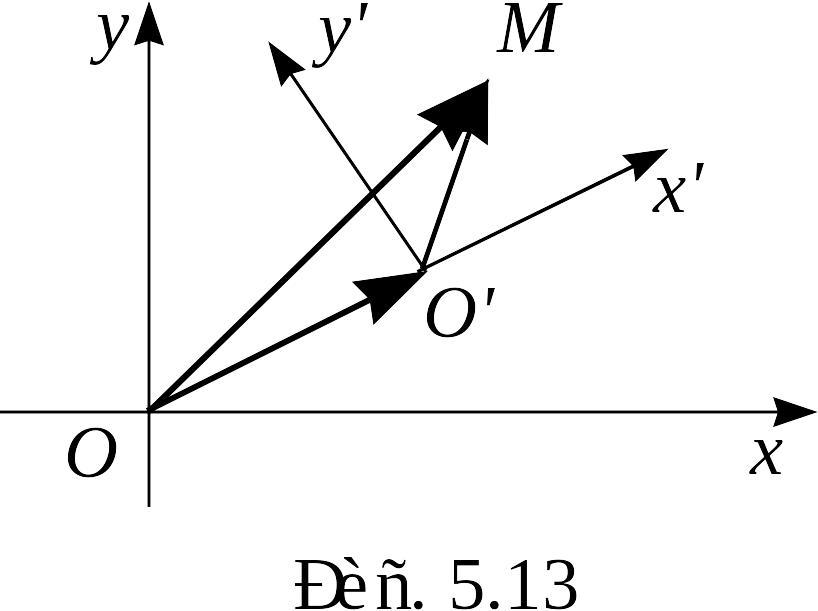 усть на плоскости заданы две произвольные декартовы системы координат (декартов базис и точка – начало координат) и (декартов базис и точка – начало координат) – обе правые (рис. 5.13).

Пусть точка имеет относительно системы координаты и , а относительно – и . Выясним, как связаны числа , и , .

Имеем , , .

Пусть точка имеет в системе координаты , следовательно, .

Таким образом,

. (5.19)

Так как – базис, найдутся числа и такие, что

(5.20)

Тогда (5.19) перепишется в виде

,

или

.

Отсюда в силу доказанной в лекции 1 теоремы 6 (о единственности разложения вектора по базису) получим

(5.21)

В равенствах (5.20) числа , , – декартовы координаты векторов и в базисе , т.е. проекции векторов и на оси векторов и .

Обозначим , тогда

, ,

,

(на рис. 5.14 одной дугой отмечены углы с соответственно перпендикулярными сторонами).

Ф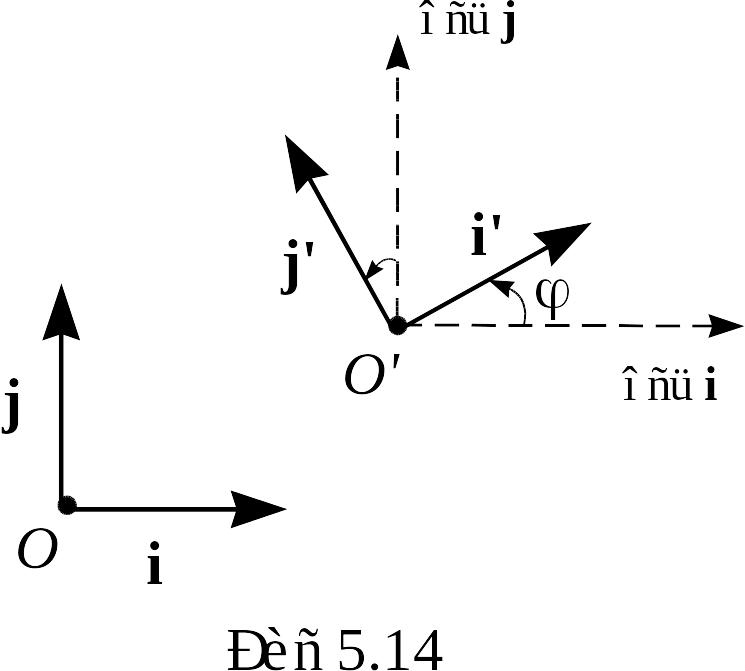 ормулы (5.21) примут вид

(5.22)

Формулы (5.22) – формулы преобразования декартовых координат.

В частности, при

– (5.23)

формулы параллельного переноса осей на вектор , а если , то формулы (5.22) примут вид

– (5.24)

формулы поворота осей на угол против хода часовой стрелки.

Замечание. Каковы бы ни были две правые системы координат и , первая из них может быть совмещена со второй посредством параллельного переноса и последующего поворота вокруг начала координат, или наоборот.

Пример 2. Установить, что уравнение

(5.25)

определяет эллипс, найти его центр и полуоси.

В самом деле, преобразуем (5.25):

, или

, или

. (5.26)

Положим

(5.27)

и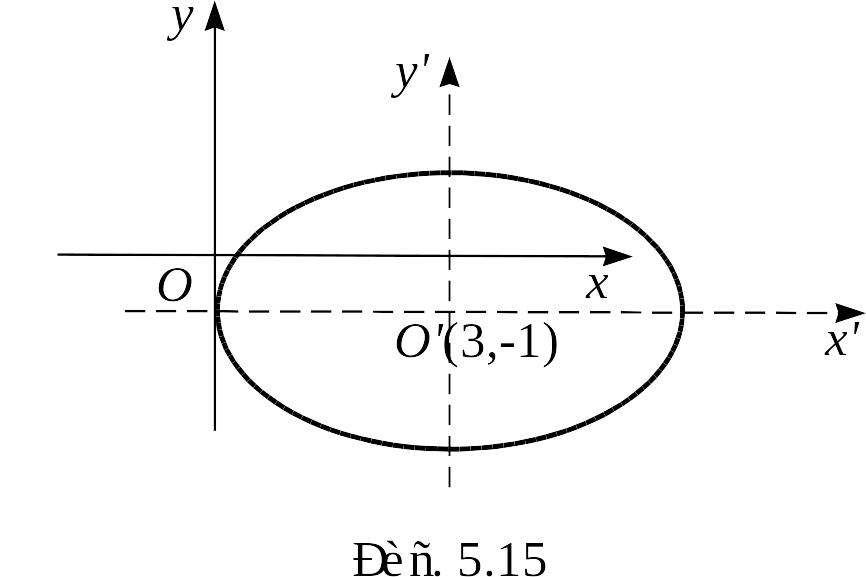 уравнение (5.26) примет вид – уравнение эллипса с полуосями и .

Формулы (5.27) – формулы параллельного переноса осей в точку . Следовательно, центр эллипса находится в точке (рис. 5.15).

Пример 3. Установить, что уравнение определяет гиперболу, найти ее центр и полуоси.

Подберем угол , после поворота на который уравнение кривой не будет содержать произведения переменных и . Подставим равенства (5.24) в заданное уравнение , или :

, или

, или

. (5.28)

Найдем такой угол , чтобы в последнем уравнении не содержалось слагаемое . Достаточно положить , т.е. , . При этом преобразование (5.24) имеет вид

–

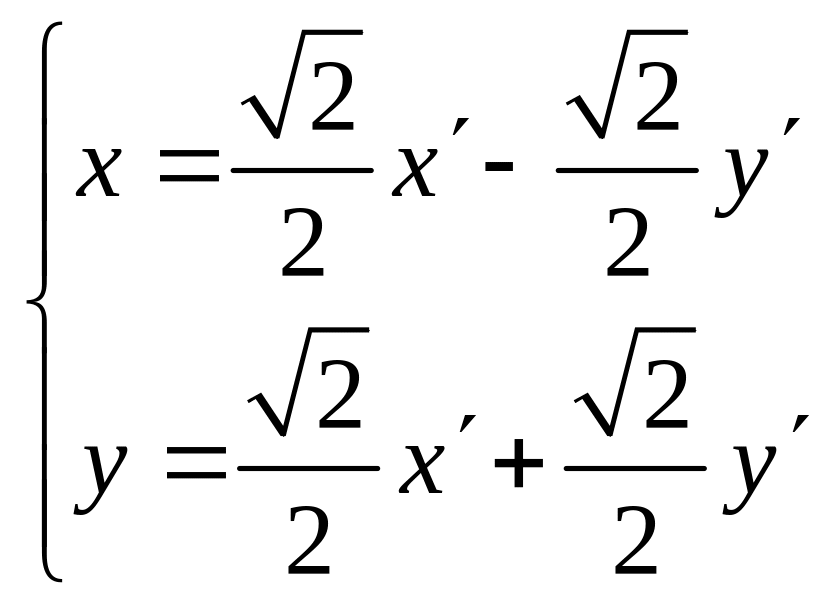поворот против часовой стрелки вокруг точки , а уравнение кривой (5.28) в новой системе координат:

–

это уравнение гиперболы с полуосями и центром в точке (рис. 5.16).