Лекции 2,3

Лекция 2

Глава 2

Скалярное, векторное и смешанное произведения

векторов

Скалярное, векторное и смешанное произведения. Определения, свойства, выражения в координатной форме

2.1. Скалярное произведение двух векторов и

его свойства

Определение 1. Скалярным произведением векторов и называется число

. (2.1)

Заметим, что в формуле (2.1)

и ,

поэтому можно дать определение скалярного произведения и в иной, равносильной форме, иногда более удобной.

Определение . Скалярным произведением векторов и называется число

. (2.2)

Геометрические свойства скалярного произведения даются теоремами 1 и 2.

Теорема 1. Два вектора и перпендикулярны тогда и только тогда, когда их скалярное произведение равно нулю.

Доказательство.

Необходимость. Пусть .

Достаточность. Пусть .

Случай 1. (либо , либо ). Так как направление не определено, считаем в этом случае, что .

Случай 2. , . В равенстве (2.1), определяющем , , , а .

Теорема 2. Для любых двух векторов и , если , , угол является острым тогда и только тогда, когда , и тупым – тогда и только тогда, когда .

Доказательство. Отметим, что, так как и , знак скалярного произведения совпадает со знаком .

Следовательно, .

Обратно, .

Аналогично, .

Обратно, .

Алгебраические свойства скалярного произведения:

1. ;

2. ;

3. ;

4. , если ; , если .

Доказательство свойства 1.

Так как и , то из формулы (2.1), определяющей скалярное произведение, непосредственно следует, что .

Доказательство свойства 2. Применяем определение (и формулу (2.2)):

.

Доказательство свойства 3. Опять привлекаем определение и формулу (2.2):

.

Доказательство свойства 4. Заметим, что , поэтому

.

Замечание 1. Свойства 2 и 3 справедливы также в форме:

) ;

) .

Действительно, например, для имеем:

.

Аналогично обосновывается ).

Доказанные алгебраические свойства дают возможность, перемножая линейные комбинации векторов, группировать коэффициенты, как при перемножении многочленов.

Пример. Пусть , , – декартов базис, , . Найти .

Имеем

.

Теорема 3. Пусть , , – декартов базис, , . Тогда .

Доказательство. Имеем

.

Следствие. Пусть , , – декартов базис, , , , . Тогда

. (2.3)

В самом деле, из формулы (2.1), определяющей скалярное произведение, находим

,

и соотношение (2.3) доказано.

В частности, .

2.2. Векторное произведение двух векторов и его свойства

Определение 2. Векторы , , называются упорядоченной тройкой или просто тройкой, если указано, какой из них является первым, какой – вторым, какой – третьим.

Запись , , будем понимать так, что – первый, – второй, – третий вектор.

Определение 3. Пусть , , не компланарны. Тройка , , называется правой (левой), если после приведения векторов , и к одному началу, вектор располагается по ту сторону от плоскости, определяемой и , откуда кратчайший поворот от к (от первого вектора ко второму) кажется совершающимся против часовой стрелки (для левой – по часовой стрелке) (рис.2.1).

Если две тройки обе правые или обе левые, они называются тройками одной ориентации, в противном случае – противоположной ориентации.

Из векторов , и можно составить шесть троек:

, , ; , , ; , , ; (2.4)

, , ; , , ; , , . (2.5)

Все тройки (2.4) – одной ориентации, и все тройки (2.5) – тоже одной ориентации, но каждая из троек (2.4) с любой тройкой (2.5) имеет противоположную ориентацию.

Упражнение. Показать, что тройки , , и , , имеют противоположную ориентацию.

Определение 4. Декартова система координат называется правой (левой), если базисные векторы , , составляют правую (левую) тройку.

Для определенности будем далее считать, что декартова система координат – правая (рис.2.2).

Определение 5. Векторным произведением вектора на вектор называется вектор , который удовлетворяет следующим трем условиям:

1) ;

2) , ;

3) тройка , , правая.

Векторное произведение будем далее обозначать .

Замечание 1. Длина равна площади параллелограмма, построенного на векторах и , приведенных к одному началу (рис.2.3).

Определение 6. Ортом вектора , , называется вектор , имеющий с одинаковое направление и такой, что .

Замечание 2. Из определения орта следует равенство .

(В самом деле, и векторы и имеют одинаковое направление.)

Замечание 3. Если – орт векторного произведения , а – площадь параллелограмма, построенного на и , приведенных к одному началу, то .

(Доказательство следует из определения 6.)

Теорема 4. Векторы и коллинеарны тогда и только тогда, когда .

Доказательство. Необходимость. Пусть и коллинеарны. Тогда

.

Достаточность. Пусть .

Случай 1. (либо , либо ). Так как направление нулевого вектора не определено, можем считать, что коллинеарен .

Случай 2. , . Так как , а и , то и коллинеарен (угол , либо ).

Алгебраические свойства векторного произведения:

1. ;

2. ;

3. ;

4. Для любого .

Доказательство свойства 1.

Обозначим , . Нам нужно доказать, что справедливо равенство между векторами:

В соответствии с определением, данным в лекции 1, нужно убедиться, что и направления и совпадают.

Из определения 5 получаем

.

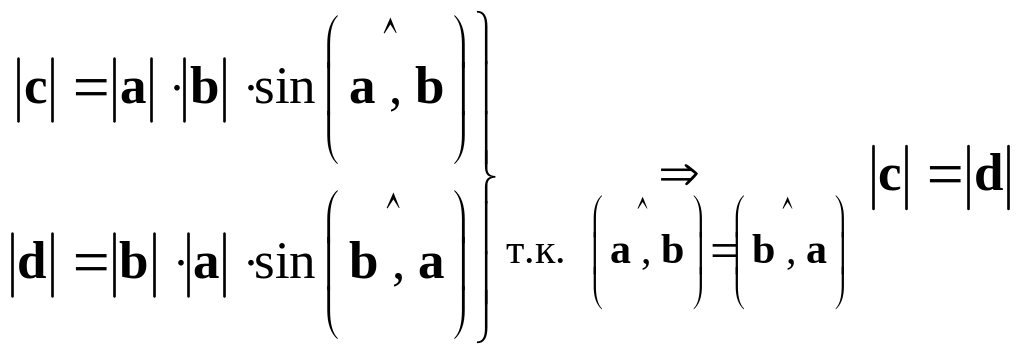По определению 5 , и , , следовательно, и оба перпендикулярны плоскости , определяемой векторами и , следовательно, и коллинеарны.

Пусть , и приведены к одному началу. Так как они составляют правую тройку, в соответствии с определением 3 с конца вектора кратчайший поворот от к кажется совершающимся против хода часовой стрелки. Тогда для любого вектора, расположенного по ту же сторону от , что и вектор , кратчайший поворот от к кажется совершающимся по ходу часовой стрелки, следовательно, вектор расположен по другую сторону от плоскости . Учитывая уже установленную коллинеарность и , получаем .

Свойство 2 примем без доказательства.

Доказательство свойства 3. Обозначим , .

Случай 1. . Тогда (так как ), при этом , следовательно, .

Случай 2. .

а) Векторы и коллинеарны. Тогда по теореме 4 и ; коллинеарен (как произведение вектора на число), следовательно, коллинеарен , и по теореме 4 , значит, .

б) Векторы и не коллинеарны. Пусть . Тогда

.

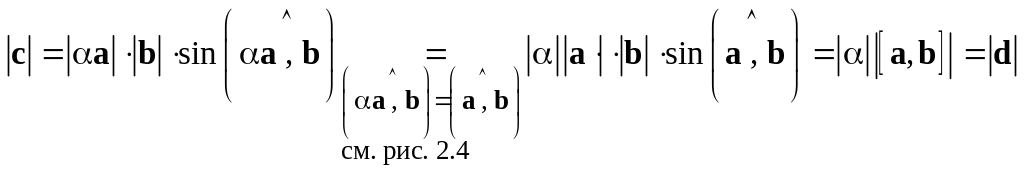
Имеем , следовательно, коллинеарен . С другой стороны, , поэтому коллинеарен . Таким образом, и коллинеарны.

Так как , а , то направление совпадает с направлением вектора .

Направление совпадает с направлением , а , следовательно, направление совпадает с направлением .

Итак, и коллинеарны и направления их совпадают, т.е. и свойство 3 в этом случае справедливо.

Пусть . Тогда

.

И меем и коллинеарен . С другой стороны и коллинеарен вектору . Таким образом, и коллинеарны (и коллинеарны вектору ).

Вектор в соответствии с определениями 5 и 3 направлен таким образом, что с конца кратчайший поворот от к кажется совершающимся против хода часовой стрелки, тогда ( ), с конца кратчайший поворот от к кажется совершающимся по ходу часовой стрелки, следовательно, векторы и имеют противоположное направление.

Вектор , равный , тоже имеет направление, противоположное направлению , таким образом, и направлены одинаково.

Учитывая доказанное ранее равенство и коллинеарность и , заключаем, что , – свойство 3 справедливо и в этом случае.

Доказательство свойства 4.

Так как любой вектор коллинеарен сам себе, то свойство 4, т.е. равенство , следует из теоремы 4.

Замечание. Свойства 2 и 3 справедливы также в форме:

). ;

). .

В самом деле, докажем, например, :

.

Аналогично обосновывается .

Доказанные алгебраические свойства дают возможность, перемножая векторно линейные комбинации векторов, группировать коэффициенты, как при перемножении многочленов.