Лекция 3
Теорема 5. Пусть
,
,
– декартов базис,
,
.
Тогда
.
Доказательство. Имеем
.
(2.6)
Найдем всевозможные векторные произведения базисных векторов.
В силу свойства 4
.
Так как базис , , декартов и длина каждого базисного вектора равна единице, каждое из оставшихся шести векторных произведений либо вектор базиса, либо противоположный ему. Векторы базиса образуют правую тройку, поэтому
,
,
,
(2.7)
а, привлекая свойство 1 и используя (2.7), получаем
,
,
,
Подставляя эти соотношения в (2.6), приходим к равенству
или
. (2.8)
Следствие. Пусть
,
,
– декартов базис,
,
.
Векторы
и
коллинеарны в том и только том случае,
когда
.
Действительно, и коллинеарны в том и только том случае (см. теорему 4), когда . Учитывая теорему 5, получаем: и коллинеарны в том и только том случае, когда
,
,
,
или
,
,
,
(2.9)
или
,
,
,
или
. (2.10)
Замечание.
Чтобы обойти трудность с равенством
нулю знаменателя в (2.10), договоримся в
том случае, когда
– координаты некоторых векторов
и
,
понимать равенство (2.10) как три равенства
(2.9).
2.3. Смешанное произведение трех геометрических векторов и его свойства
Определение 7. Пусть
.
Скалярное произведение одного из
векторов на векторное произведение
двух других называется смешанным
произведением векторов
,
и
.
Запись:
.
Теорема 6.
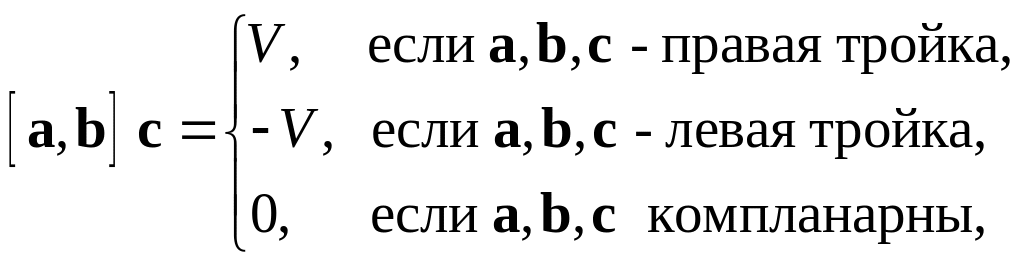
где
– объем параллелепипеда, построенного
на приведенных к одному началу векторах
,
и
.
Доказательство. Случай
1. Векторы
и
коллинеарны
скалярное произведение
.
Но при этом, так как
и
коллинеарны, система
,
линейно зависима (см. теорему 3 в лекции
1), следовательно, по Теореме 2 из Лекции
1 система векторов
,
,
линейно зависима, как содержащая линейно
зависимую подсистему. Поэтому (см.
теорему 4 в Лекции 1)
,
,
компланарны. Таким образом, теорема 6 в
этом случае справедлива.
Случай 2. и не коллинеарны. Приведем и к одному началу. Пусть – площадь параллелограмма, построенного на и как на сторонах, а - орт вектора . Тогда в силу замечания 3 .
Тогда
.
а) , , компланарны.
Приведем и
к тому же началу (рис.2.6). Так как
,
то
,
следовательно,
.
б) , , не компланарны.
Приведем , и к одному началу и рассмотрим параллелепипед, натянутый на , и (рис.2.7).
Обозначим через
высоту получившегося параллелепипеда.
Имеем
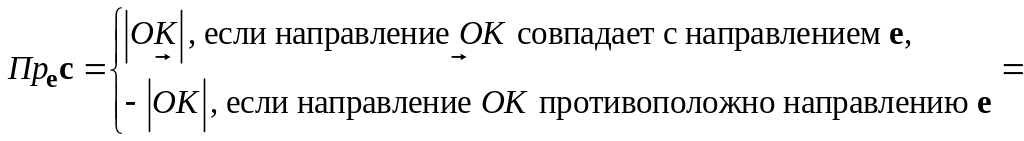
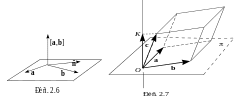
Следовательно,
и теорема 6 доказана.
Следствие 1. Справедливо равенство
.
(2.11)
В самом деле, если , и компланарны, то по теореме 6 все три числа равны нулю.
Если же векторы
,
и
не компланарны, то поскольку тройки
,
и
– одной ориентации, либо все числа в
равенстве (2.11) равны объему
одного и того же параллелепипеда (если
тройки правые), либо равны
(если тройки левые).
Замечание. В силу равенства (2.11) принято опускать скобки в записи смешанного произведения:
.
Следствие 2. Векторы
,
и
компланарны в том и только том случае,
когда
.
Доказательство. Необходимость. Пусть , и компланарны, тогда (по теореме 6) .
Достаточность.
Пусть
.
Вернемся к определению 7:
.
Случай 1.
и
коллинеарны
и
линейно зависимы
система
векторов
,
,
линейно зависима
,
,
компланарны.
Случай 2. Пусть
,
а
.
Н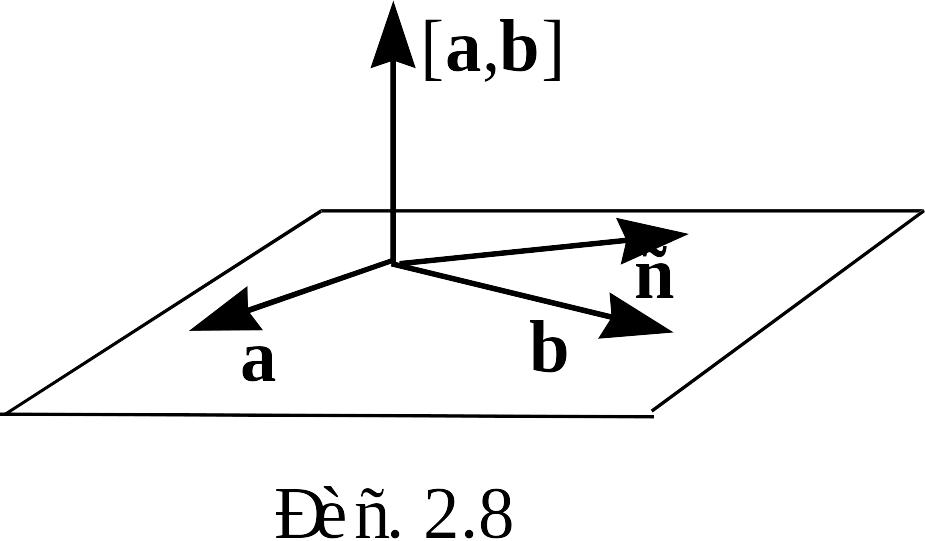
о
по определению векторного произведения
и
.
Таким образом, , , принадлежат плоскости , перпендикулярной к . Следовательно, векторы , , компланарны (рис.2.8).
Теорема 7. Пусть
,
,
– декартов базис,
,
,
.
Тогда
.
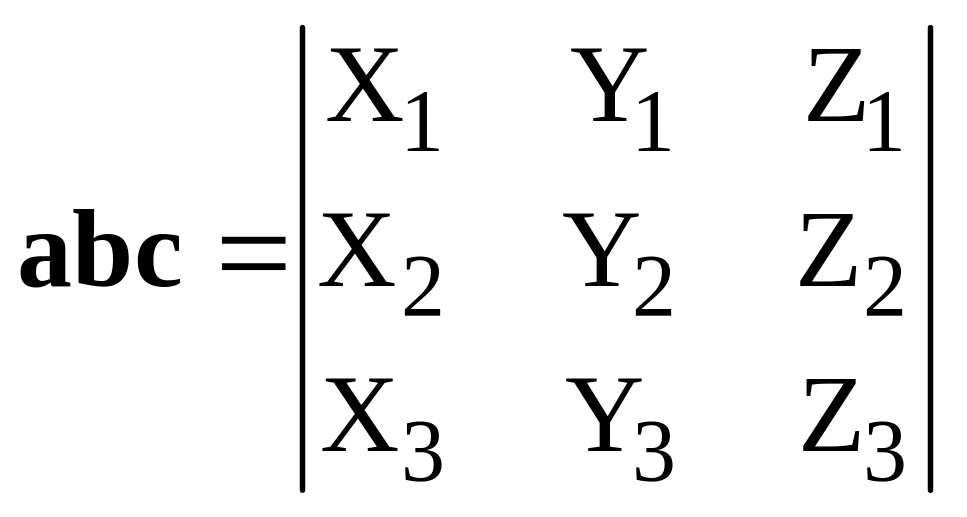Доказательство. Вернемся к
записи смешанного произведения в
соответствии с определением 7:
.
По доказанному (см. теорему 5)
.
Далее имеем
,
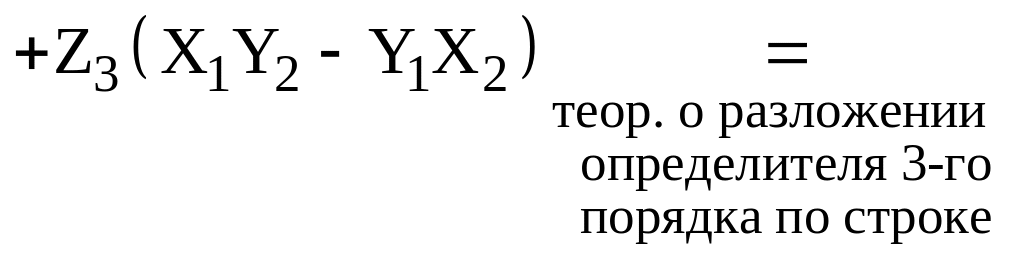
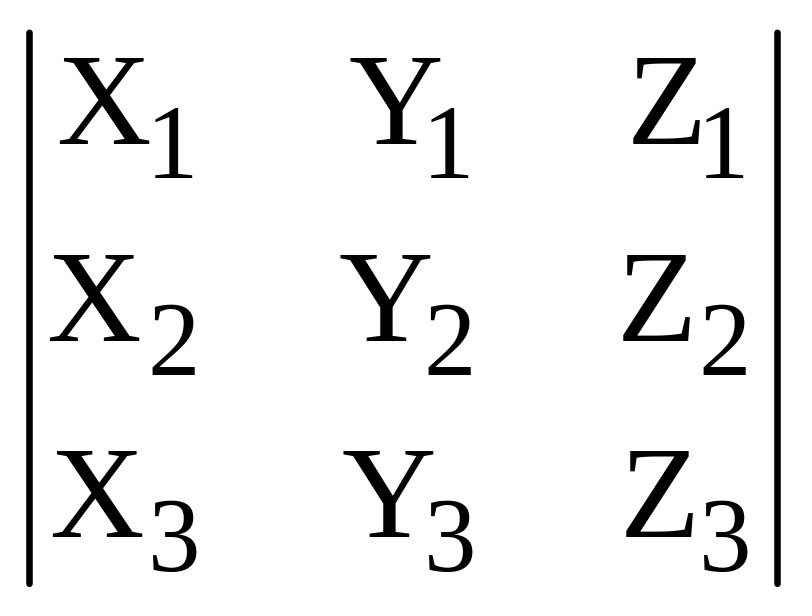и теорема 7 доказана.