5.2. Гипербола

Определение 3. Гиперболой называется геометрическое место точек плоскости, для каждой из которых абсолютная величина разности расстояний до двух фиксированных точек этой плоскости, называемых фокусами, есть величина постоянная.

Обозначим фокусы через и , постоянную, о которой говорится в определении, – через . Тогда

гиперболе . (5.8)

Введем систему координат. Пусть ось проходит через точки и , ось – через середину отрезка перпендикулярно оси .

Пусть (рис. 5.5).

Точка принадлежит гиперболе тогда и только тогда, когда

или

. (5.9)

Преобразуем (5.9). Дважды возведя в квадрат обе части и приведя подобные слагаемые, придем к равенству

. (5.10)

В разность двух сторон меньше третьей стороны: , т.е. и . Тогда , обозначим . Уравнение (5.10) примет вид , или

. (5.11)

Пусть точка такова, что и удовлетворяют уравнению (5.11), тогда

, (5.12)

и имеем

.

Сравним абсолютные величины и .

Из уравнения (5.11) , т.е. , тогда , отсюда .

Аналогичные преобразования дают

Таким образом,

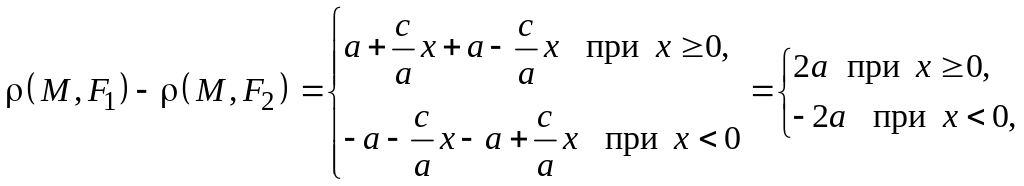
или и точка принадлежит гиперболе, следовательно, уравнение (5.11) – уравнение гиперболы.

Уравнение (5.11) называется каноническим уравнением гиперболы, числа и в уравнении (5.11) - соответственно «действительной» и «мнимой» полуосями гиперболы.

Исследуем форму гиперболы по ее каноническому уравнению.

Утверждение 3. Гипербола имеет две оси симметрии и центр симметрии.

В самом деле, если принадлежит гиперболе, то принадлежит гиперболе (так как входит в уравнение (5.11) в четной степени) и принадлежит гиперболе (так как входит в уравнение (5.11) в четной степени), но тогда и принадлежит гиперболе, а это и означает, что гипербола симметрична относительно осей и , а также начала координат (рис. 5.6).

Определение 4. Две взаимно перпендикулярные оси симметрии гиперболы называются главными осями гиперболы, а центр симметрии - центром гиперболы.

Точки пересечения гиперболы с одной из главных осей называются вершинами гиперболы: , . Та из главных осей гиперболы, которая имеет с ней общие точки, называется действительной осью, другая – мнимой.

Замечание. Фокусы гиперболы располагаются на ее действительной оси.

Так как для точек гиперболы , в области (в полосе, ограниченной прямыми ), точек гиперболы нет.

Как и для эллипса, прямоугольник, ограниченный прямыми и , называется основным прямоугольником. Его диагонали задаются уравнениями .

Определение 5. Пусть для функции существует такая прямая , что при бесконечном удалении точки от начала координат, тогда эта прямая называется асимптотой графика функции .

Утверждение 4. Прямые являются асимптотами гиперболы.

Ограничимся рассмотрением области , (I четверть), так как имеет место осевая симметрия.

Из уравнения (5.11)

. (5.14)

Зафиксируем (рис. 5.7), точка лежит на гиперболе, а – на прямой , .

.

Имеем

,

следовательно, при и в соответствии с определением 5 прямая – асимптота гиперболы (5.11).

Построим гиперболу (5.11) в I четверти и затем воспользуемся установленной симметрией относительно осей и .

Из (5.14) следует, что при возрастании от до переменная возрастает от до .

Суммируя все приведенные соображения, получим «эскиз» гиперболы вначале в I четверти, а затем на всей плоскости (рис. 5.8).