Лекции 6 и 7

Лекция 6

Глава 5

Кривые и поверхности второго порядка

Вывод канонических уравнений эллипса, гиперболы и параболы. Исследование их формы по каноническому уравнению. Преобразование декартовых прямоугольных координат на плоскости. Классификация поверхностей второго порядка по каноническим уравнениям. Метод сечений.

5.1. Эллипс

Определение 1. Эллипсом называется геометрическое место точек плоскости, для каждой из которых сумма расстояний до двух фиксированных точек этой плоскости, называемых фокусами, есть величина постоянная.

Обозначим фокусы через и , постоянную, о которой говорится в определении, через – через . Тогда

эллипсу . (5.1)

В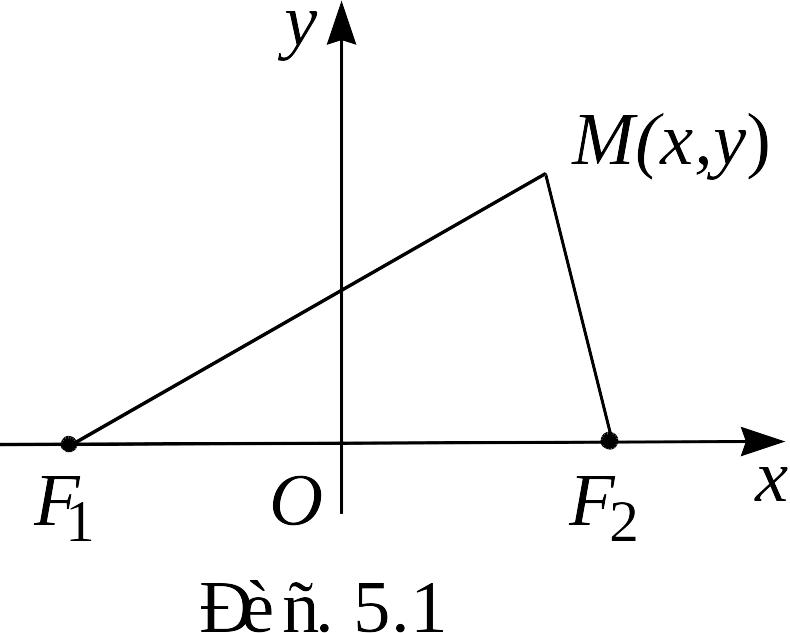 ведем систему координат. Пусть ось абсцисс проходит через точки и , ось ординат – через середину отрезка перпендикулярно оси абсцисс (рис. 5.1).

Пусть .

Точка принадлежит эллипсу тогда и только тогда, когда выполнено равенство

. (5.2)

Преобразуем уравнение (5.2):

и после приведения подобных слагаемых получим

.

Еще раз возведем обе части в квадрат и получим:

, или

. (5.3)

В , т.е. и . Тогда обозначим .

Уравнение (5.3) перепишется в виде , или

. (5.4)

Пусть точка такова, что и удовлетворяют уравнению (5.4), тогда

. (5.5)

Имеем

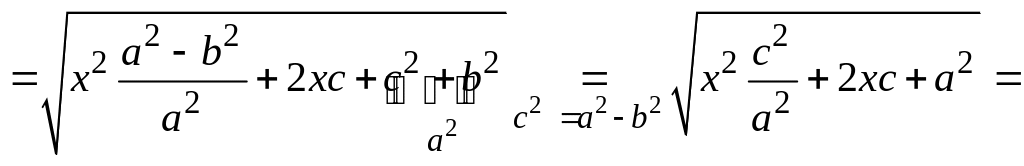
. (5.6)

Сравним абсолютную величину и , чтобы опустить знак модуля в (5.6). Из уравнения (5.4) , т.е. , тогда и .

Аналогичные преобразования дают

. (5.7)

Таким образом, , следовательно, точка принадлежит эллипсу, и уравнение (5.4) – уравнение эллипса.

Уравнение (5.4) называется каноническим уравнением эллипса, числа и в уравнении (5.4) – соответственно его «большой» и «малой» полуосями.

Исследуем форму эллипса по его каноническому уравнению.

Утверждение 1. Эллипс имеет две оси симметрии и центр симметрии.

Д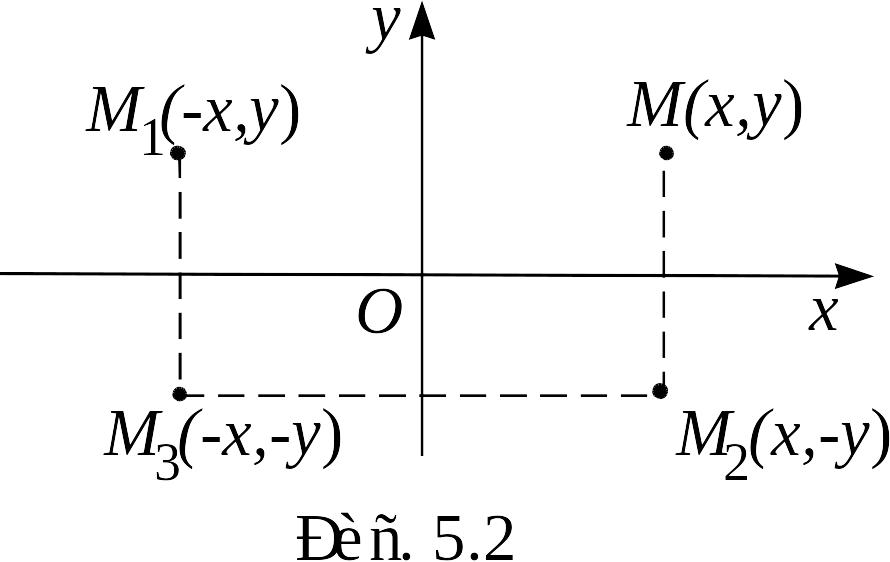 ействительно, если принадлежит эллипсу, то принадлежит эллипсу (так как входит в уравнение (5.4) в четной степени) и принадлежит эллипсу (так как входит в уравнение (5.4) в четной степени), но тогда и принадлежит эллипсу, а это и означает, что эллипс симметричен относительно осей и , а также начала координат (рис. 5.2).

Определение 2. Две взаимно перпендикулярные оси симметрии эллипса называются его главными осями, центр симметрии эллипса называется центром эллипса.

Точки пересечения эллипса с главными осями называются вершинами эллипса: , , и ; отрезки и – большой и малой осями эллипса (при большой осью будет , а малой - ).

Замечание. Фокусы эллипса располагаются на его большой оси.

Утверждение 2. Весь эллипс содержится внутри прямоугольника, ограниченного прямыми и .

Этот прямоугольник называется основным прямоугольником эллипса (рис. 5.3).

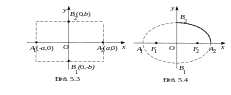
В самом деле, так как , то ; оценка была получена выше (неравенство (5.7)).

Построим эллипс в I четверти и, пользуясь симметрией, отразим график сначала, например, относительно оси (в IV четверть), а затем то, что получится, в III и II четверти.

Из уравнения (5.4) имеем

.

Отметим, что при возрастании от до переменная убывает от до .

Все приведенные соображения обеспечивают возможность нестрогого построения эллипса («эскиза» кривой), определенного уравнением (5.4) (рис. 5.4).

Замечание. При эллипс представляет собой окружность с центром в начале координат и радиусом : (Фокусы и при этом совпали с центром ( ).)