3.6. Нормированное уравнение прямой. Расстояние от точки до прямой
П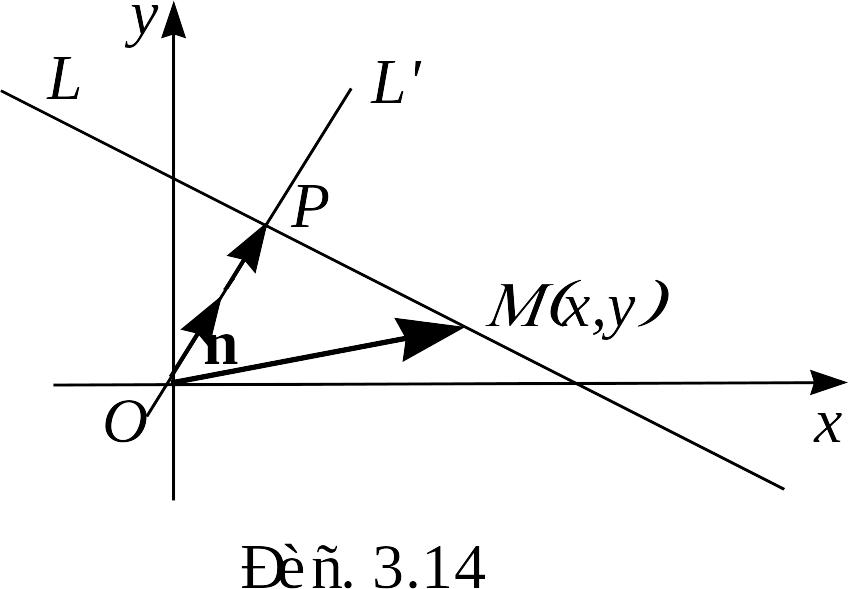
усть
задана декартова система координат
,
- произвольная прямая (рис. 3.14). Проведем
через
прямую
,
,
точку пересечения
с
обозначим
.
Рассмотрим
вектор
:
приложен к точке
,
,
направление
совпадает с направлением вектора
(если
,
направление
выберем произвольно). Обозначим через
угол наклона
к оси
.
Тогда
.
Длину
обозначим через
:
.
Имеем
;
(3.19)
;
(3.20)
.
(3.21)
Из
(3.19), (3.20) и (3.21) получим:
или
.
(3.22)
Уравнение
(3.22) называется нормированным
уравнением
прямой
(
- угол наклона вектора
,
)
к оси
,
- расстояние от начала координат
до
).
Приведем без доказательства следующее утверждение.
Теорема
3.
Расстояние
от точки
до прямой
равно абсолютной величине результата
подстановки координат этой точки
и
в левую часть нормированного уравнения
прямой
:
.
Замечание. Если прямая задана общим уравнением
, (3.23)
то
для перехода к уравнению вида (3.22) нужно
обе части (3.23) умножить на нормирующий
множитель
.
Знак
выбирается противоположным знаку
в (3.23).
В
самом деле, пусть уравнения
и
определяют одну и ту же прямую
.
Тогда (см. замечание в 3.2) существует
такое число
,
что
,
,
,
а
.
Из
равенства
следует, что знаки
и
противоположны (
).
Пример
4.
Найти расстояние от точки
до прямой
.
Имеем
.
Нормированное уравнение заданной
прямой:
,
.