1.4. Проекция вектора на ось
Осью назовем прямую с указанным на ней направлением.
Определение 10. Пусть
- произвольный вектор,
- ось. Проведем через начало и конец
вектора
плоскости, перпендикулярные оси
,
пусть точки пересечения этих плоскостей
с осью –
и
.
Рис. 1.16 поясняет определение 10.
Определение 11. Углом наклона вектора к оси называется наименьший угол между двумя выходящими из произвольной точки лучами, один из которых имеет направление, совпадающее с направлением оси , другой – направление, совпадающее с направлением вектора .
На рис. 1.17, поясняющем определение 11,
угол наклона
к оси
,
который в дальнейшем будем обозначать
,
отмечен двумя дугами.
Теорема 8. Пусть
– произвольная ось,
.
Тогда
.
Доказательство. Обозначим через
– ось, проходящую через точку
,
начало вектора
,
и имеющую направление оси
.
Тогда углом наклона вектора
к оси
будет согласно определению 11, угол
(рис.
1.18).
Случай 1.
Направление
совпадает с направлением оси
(а следовательно, и
).
Тогда
.
Случай 2. Направление противоположно направлению оси (т.е. и тоже). Тогда
.
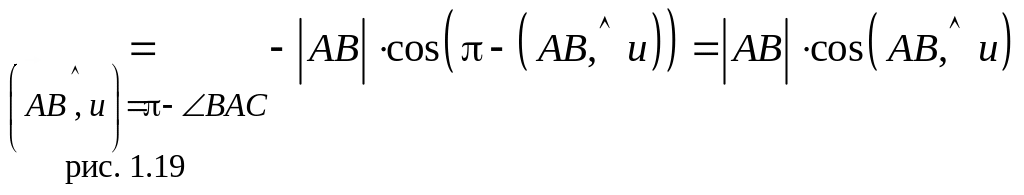Теорема 8 доказана.
1.5. Декартов базис и декартовы координаты
Определение 12. Углом между векторами и будем называть наименьший из двух углов, образованных выходящими из произвольной точки лучами, один из которых имеет направление, совпадающее с направлением , другой – направление, совпадающее с направлением .
Если векторы коллинеарны, угол считаем
равным нулю, если их направления
совпадают, и равным
,
если направления
и
противоположны.
Рис. 1.20 поясняет определение 12.
У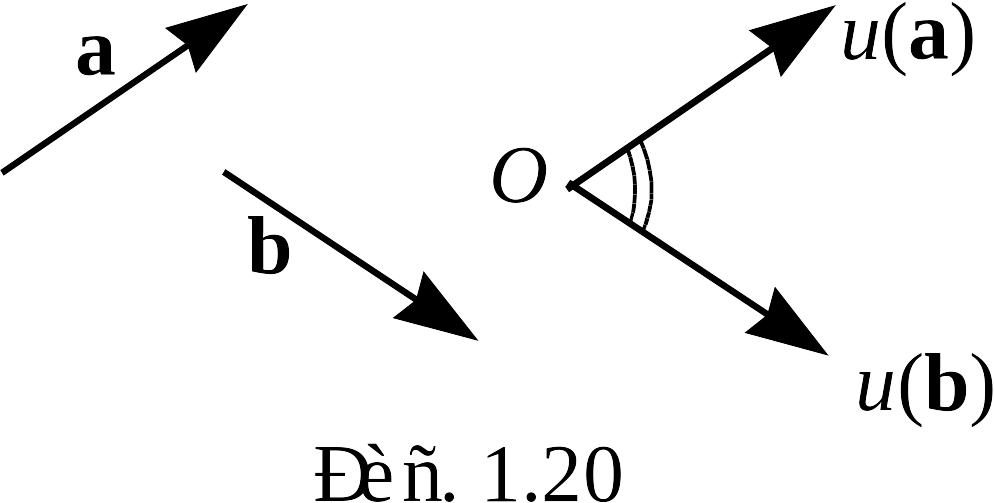
гол
между векторами
и
в дальнейшем будем обозначать
,
на рис. 1.20 угол
отмечен двумя дугами.
Определение 13. Базис , , называется декартовым прямоугольным базисом, если:
1)
,
и
;
2)
.
Обычно в литературе векторы декартова
базиса обозначают через
,
,
и слово «прямоугольный» опускают.
Пусть
,
,
– некоторый декартов базис,
.
Тогда найдутся числа
такие, что
.
(1.12)
Числа
называют декартовыми прямоугольными
координатами вектора
.
Будем использовать в дальнейшем запись
,
равносильную записи (1.12) в виде разложения
вектора по базису.
Декартова система координат определяется в пространстве заданием декартова базиса , , и некоторой точки – точки приложения векторов базиса. Точка называется началом координат.
Определение 14. Пусть задана
декартова система координат. Декартовыми
координатами произвольной точки
называются координаты вектора
относительно базиса
,
,
.
По доказанной теореме 6 координаты вектора относительно базиса , , определяются однозначно, поэтому, если задана система координат (точка – начало координат и декартов базис , , ), то каждой точке пространства однозначно соответствует тройка декартовых координат .
Отметим, что свойства базиса и декартовых координат точки на плоскости и прямой аналогичны случаю пространства.
Геометрический смысл декартовых координат вектора устанавливается следующей теоремой.
Теорема 9. Пусть
,
,
– декартов прямоугольный базис,
.
Тогда
,
,
.
Доказательство. Приведем векторы
,
,
и
к одному началу, некоторой точке
,
и через конец вектора
проведем плоскости, соответственно
параллельные парам векторов:
и
,
и
,
и
,
получим прямоугольный параллелепипед
,
в котором диагональ
(рис. 1.21).
В силу теоремы 6 о единственности разложения по базису
.
(1.13)
Имеем
(1.14)
В соответствии с определением 10
(1.15)
Если направление
совпадает с направлением
,
то в (1.13) по определению произведения
вектора на число
.
Тогда в (1.14)
,
и в (1.15)
.
Если направление
противоположно направлению
,
то в (1.13)
.
Следовательно, в (1.14)
,
а в (1.15)
.
Таким образом, в обоих случаях .
Аналогично,
,
.
Теорема 9 доказана.
Пусть задана произвольная декартова система координат (точка – начало координат и декартов базис , , ).
Обозначим через
,
,
– оси, направление которых совпадает
с направлением векторов
,
,
соответственно. Пусть
,
обозначим через
,
,
– углы наклона вектора
к осям
,
,
соответственно.
Числа
,
,
называются направляющими косинусами
вектора
.
Пусть . Имеем
,
,
.
(1.16)
Было доказано (см. теорему 6), что вектор однозначно определяется заданием своих координат. Равенства (1.16) означают, что однозначно определяется заданием длины и трех направляющих косинусов.
Получим еще некоторые полезные при решении задач соотношения.
Так как параллелепипед на рис. 1.21 прямоугольный, то
.
Тогда имеем,
,
,
,
откуда
(сумма квадратов направляющих косинусов
любого вектора равна единице).
Теорема 10 (линейные свойства проекции). Проекция суммы любых двух векторов на произвольную ось равна сумме проекций; при умножении вектора на число проекция умножается на это число.
Доказательство. Пусть
– произвольная ось,
и
– произвольные векторы.
Рассмотрим декартов прямоугольный
базис такой, что ось
совпадает с осью вектора
.
Пусть
,
.
Имеем
.
.
(1.17)
С другой стороны,
,
.
(1.18)
Сравнив (1.17) и (1.18) заключаем
.
Аналогично, если
– произвольное действительное число,
то
,
,
а, значит,
.