testy_ozz_OSENNIJ_SEMESTR

МОДУЛЬ 1.1.

1. Назовите виды статистической совокупности:

1) выборочная, минимальная;

2) генеральная, максимальная;

3) выборочная, генеральная;

4) атипичная, произвольная;

5) генеральная, типичная.

2. Дайте определение генеральной совокупности:

1) совокупность, состоящая из большого числа единиц наблюдения;

2) множество качественно однородных единиц наблюдения, объединенных одним или группой признаков;

3) множество единиц наблюдения;

4) совокупность, которая позволяет выявить общие закономерности изучаемого явления;

5) множество статистических величин.

3. Что является объектом статистического исследования?

1) единица наблюдения;

2) атрибутивные признаки;

3) количественные признаки;

4) статистическая совокупность;

5) факторные и результативные признаки.

4. С чего начинается статистическое исследование?

1) с разработки программы и рабочего плана исследования;

2) разработки программы сбора и обработки данных;

3) выработки управленческих решений;

4) определения единиц наблюдения;

5) определения объекта наблюдения.

5. Чем определяется выбор единицы наблюдения?

1) программой исследования;

2) заданием руководителя органа управления здравоохранением;

3) рабочим планом;

4) объемом статистической совокупности;

5) видом статистического исследования.

6. Какие из перечисленных характеристик относятся только к количественным учетным признакам единиц наблюдения?

1) диагноз, время госпитализации, место рождения, место госпитализации;

2) возраст, дата поступления и выписки, количество койко-дней, данные лабораторных исследований, пульс, давление, частота дыхания, доза лекарственных препаратов;

3) диагноз, фамилия, пол, исход лечения, семейное положение;

4) исход лечения, количество койко-дней, пол, методы лечения, семейное положение;

5) диагноз, методы лечения, доза лекарственных препаратов, время госпитализации.

7. Назовите виды статистических наблюдений в зависимости от полноты охвата:

1) сплошное, выборочное;

2) полное, неполное;

3) выборочное, полное;

4) сплошное, неполное;

5) генеральное, случайный отбор.

8. Макет какой таблицы изображен на рисунке?

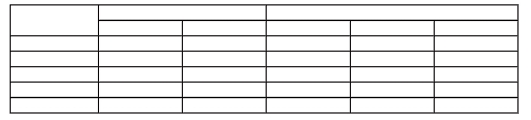
1) простой;

2) сложной;

3) групповой;

4) комбинационной;

5) единичной.

9. В содержание первого этапа статистического исследования входит все нижеперечисленное, кроме:

1) определения цели и задач исследования;

2) выбора единицы наблюдения;

3) определения объекта исследования;

4) контроля входных данных;

5) составления плана исследования.

10. В содержание второго этапа статистического исследования входит все нижеперечисленное, кроме:

1) формирования баз данных;

2) выкопировки данных;

3) анкетирования или опроса;

4) контроля входных данных;

5) статистического анализа данных.

11. В содержание третьего этапа статистического исследования входит все нижеперечисленное, кроме:

1) подготовки данных;

2) группировки данных;

3) априорного анализа данных;

4) визуализации данных;

5) составления программы исследования.

12. В содержание четвертого этапа статистического исследования входит все нижеперечисленное, кроме:

1) разработки альтернативных вариантов решения проблемы;

2) экономического обоснования выбранного решения;

3) составления макетов статистических таблиц;

4) согласования выбранного решения с вышестоящим органом управления;

5) контроля за выполнением управленческого решения.

13. Макет какой таблицы изображен на рисунке?

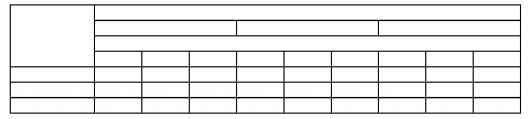
1) простой;

2) сложной;

3) групповой;

4) комбинационной;

5) единичной.

14. Что предусматривает рабочий план статистического исследования?

1) определение объекта исследования;

2) способы формирования выборочной совокупности;

3) формулировку гипотез;

4) составление сетевого графика;

5) постановку цели и задач исследования.

15. Макет какой таблицы изображен на рисунке?

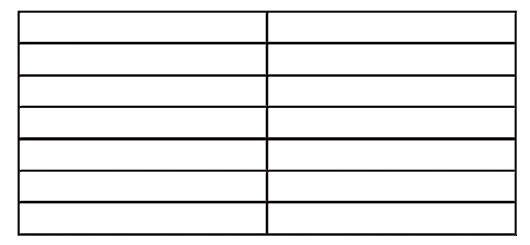
1) простой;

2) сложной;

3) групповой;

4) комбинационной;

5) единичной.

МОДУЛЬ 1.2.

1. Что такое абсолютный статистический показатель?

1) показатель, имеющий определенную размерность и единицу измерения;

2) показатель, дающий качественную характеристику изучаемого явления;

3) показатель, используемый для сравнения и сопоставления совокупностей;

4) наиболее точный, достоверный показатель, характеризующий данное явление;

5) показатель, используемый для обобщающей характеристики совокупности.

2. Для характеристики частоты явления следует применять показатели:

1) соотношения;

2) экстенсивные;

3) интенсивные;

4) наглядности;

5) динамические ряды.

3. Для чего используют экстенсивные показатели?

1) чтобы наглядно показать различия сравниваемых групп;

2) дать характеристику ряда, состоящего из однородных сопоставляемых величин;

3) показать долю части в целом;

4) судить о частоте явления;

5) показать частоту явления в динамике.

4. Назовите способ вычисления экстенсивного показателя:

1) отношение числа, выражающего величину данного явления к величине всей совокупности;

2) отношение значений двух самостоятельных совокупностей;

3) отношение ряда чисел к одному из них, принимаемому за 100%;

4) отношение абсолютного уровня последующего числа к предыдущему в процентах;

5) отношение каждой последующей относительной величины к последующей в процентах.

5. Назовите способ вычисления показателя наглядности:

1) отношение числа, выражающего величину данного явления, к величине всей совокупности;

2) отношение части явления к целому явлению;

3) отношение ряда сравниваемых однородных величин к одной из них, принятой за 100%;

4) отношение абсолютного уровня последующего числа к предыдущему, выраженное в процентах.;

5) отношение каждой последующей относительной величины к предыдущей, выраженное в процентах.

6. Укажите, какому из приведенных ниже определений соответствует показатель соотношения:

1) изменение явления во времени;

2) распределение целого по частям;

3) уровень, распространенность явления в среде, непосредственно (биологически) не связанного с данной средой;

4) сопоставление ряда однородных величин, имеющих разный характер;

5) частота явления в среде, непосредственно с ним связанной.

7. Укажите, какому из приведенных ниже определений соответствует интенсивный показатель:

1) изменение явления во времени;

2) распределение целого по частям;

3) уровень, распространенность какого-либо явления в среде, непосредственно связанного с данной средой;

4) характеристика явления в среде, непосредственно с ним не связанной;

5) сопоставление ряда однородных, но имеющих разный размер величин.

8. Какой показатель можно использовать для изучения распределения больных по возрасту?

1) интенсивный;

2) экстенсивный;

3) наглядности;

4) соотношения;

5) динамические ряды.

9. Назовите показатель, характеризующий частоту случаев заболеваний среди населения:

1) экстенсивный;

2) интенсивный;

3) динамические ряды;

4) соотношения;

5) наглядности.

10. Назовите показатель, характеризующий обеспеченность населения койко-местами в лечебных учреждениях:

1) интенсивный;

2) экстенсивный;

3) наглядности;

4) соотношения;

5) динамические ряды.

11. Дайте определение относительного статистического показателя:

1) показатель, характеризующий структуру явлений;

2) показатель, выражающий количественное соотношение между явлениями;

3) показатель взаимодействия двух величин;

4) показатель, отражающий свойства генеральной совокупности;

5) показатель, характеризующий размер количественных и качественных признаков.

12. Численность населения города - 150 000 человек. Врачей - 110. Какой показатель можно рассчитать из приведенных данных?

1) интенсивный;

2) экстенсивный;

3) соотношения;

4) наглядности;

5) динамические ряды.

13. Из 4000 случаев заболеваний, зарегистрированных в поликлинике, 300 - сердечно-сосудистые. Какой показатель можно рассчитать из приведенных данных?

1) интенсивный;

2) экстенсивный;

3) соотношения;

4) наглядности;

5) динамические ряды.

14. Численность населения города - 120 000 человек. Зарегистрировано 5190 случаев заболеваний. Какой показатель можно рассчитать из приведенных данных?

1) интенсивный;

2) экстенсивный;

3) соотношения;

4) наглядности;

5) динамические ряды.

Модуль 1.3.

1. Дайте определение средней величины:

1) число, выражающее общую меру количественного признака в совокупности;

2) величина, отражающая общее свойство статистической совокупности;

3) величина, представляющая собой обобщенную количественную характеристику статистической совокупности;

4) величина, показывающая размер признаков в расчете на единицу однородной совокупности;

5) величина, дающая серединную характеристику признака.

2. Дайте определение вариационного ряда:

1) ряд наблюдений (выборка), все элементы которого упорядочены по возрастанию;

2) два ряда величин, изменяющихся в убывающем или возрастающем порядке;

3) ряд числовых значений какого-то определенного количественного порядка;

4) статистический ряд, характеризующийся распределением чисел в убывающем или возрастающем порядке;

5) ряд чисел, характеризующий определенный признак.

3. Дайте определение средней арифметической простой:

1) средняя, которая определяет количество вариант в вариационном ряду;

2) средняя, которая характеризует распределение вариант в вариационном ряду;

3) средняя, которая получается как частное от деления суммы вариант на сумму частот;

4) средняя вариационного ряда, вычисляемая по формуле:

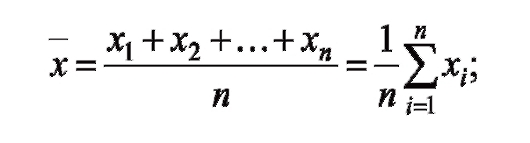
5) средняя вариационного ряда, вычисляемая по формуле:

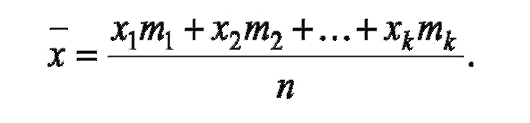
4. Какая из перечисленных величин не относится к средним величинам?

1) мода;

2) медиана;

3) средняя арифметическая;

4) средняя простая;

5) средняя геометрическая.

5. Вариантой называют:

1) любое числовое значение нескольких признаков;

2) элемент характеристики изучаемых признаков;

3) элемент вариационного ряда;

4) частоту вариационного ряда;

5) числовое значение абсолютных величин.

6. Дайте определение средней арифметической взвешенной:

1) средняя, которая определяет количество вариант в вариационном ряду;

2) средняя, которая характеризует распределение вариант в вариационном ряду;

3) средняя, которая получается как частное от деления суммы вариант на сумму частот;

4) средняя вариационного ряда, вычисляемая по формуле:

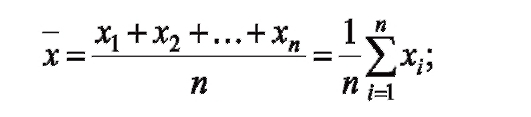
5) средняя вариационного ряда, вычисляемая по формуле:

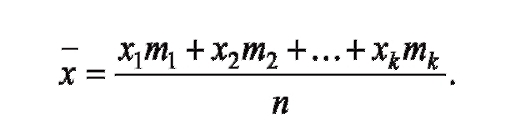
7. Средние величины используются:

1) для анализа показателей частоты распространения явлений в своей среде;

2) получения обобщенной характеристики изучаемого признака;

3) определения уровней здоровья населения;

4) изучения структуры изучаемых совокупностей;

5) изучения структуры изучаемых явлений.

8. Какая характеристика общественного здоровья выражается средними величинами?

1) рождаемость;

2) заболеваемость;

3) средняя продолжительность предстоящей жизни;

4) физическое здоровье;

5) инвалидность.

Модуль1.4.

1. Какая совокупность называется генеральной?

1) достоверные данные, необходимые для исследования;

2) отдельные единицы совокупности, отличающиеся друг от друга в силу различных случайных причин;

3) неограниченное число единиц наблюдения;

4) множество статистических элементов;

5) множество качественно однородных единиц наблюдения, объединенных по одному или группе признаков.

2. Часть единиц наблюдения генеральной совокупности, которая подвергается выборочному исследованию, называют:

1) частичной совокупностью;

2) случайной совокупностью;

3) выборочной совокупностью;

4) общей совокупностью;

5) фрагментарной совокупностью.

3. Назовите важнейшее условие объединения единиц наблюдения в выборочную совокупность:

1) репрезентативность;

2) однородность;

3) разнообразие;

4) конгруэнтность;

5) случайность.

4. Какие ошибки возникают вследствие того, что выборочная совокупность не воспроизводит в точности характеристики генеральной совокупности?

1) ошибки выборки;

2) ошибки регистрации;

3) непреднамеренные ошибки;

4) логические ошибки;

5) систематические ошибки.

5. Возможное расхождение характеристик выборочной и генеральной совокупностей измеряют:

1) средним квадратическим отклонением;

2) дисперсией;

3) ошибкой выборки;

4) корреляцией;

5) ошибкой регистрации.

6. Чем обеспечивается репрезентативность выборки?

1) случайным отбором;

2) ошибкой выборки;

3) предельной ошибкой;

4) средним квадратическим отклонением;

5) случайной ошибкой.

7. Что такое серийный отбор?

1) отбор копи-пар единиц наблюдения;

2) отбор единиц наблюдений с помощью генератора случайных чисел;

3) отбор целых групп единиц наблюдения;

4) многоступенчатый отбор единиц наблюдения;

5) типологический отбор единиц наблюдения.

8. Укажите формулу для вычисления предельной ошибки выборки:

Ответ 4

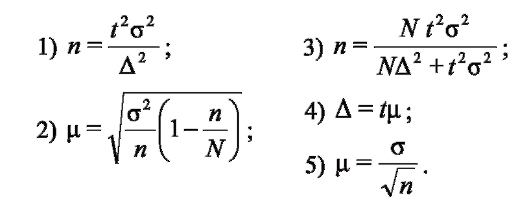
9. В каких случаях используется когортный метод?

1) для изучения заболеваемости населения;

2) анализа причинно-следственных связей заболеваемости и факторов риска;

3) разработки целевых медико-социальных программ;

4) изучения статистической совокупности относительно однородных групп лиц, объединенных наступлением определенного демографического события;

5) анализа социальной эффективности деятельности системы здравоохранения.

10. Необходимый объем выборки, обеспечивающий заданную точность, определяется по формуле:

ОТВЕТ 3

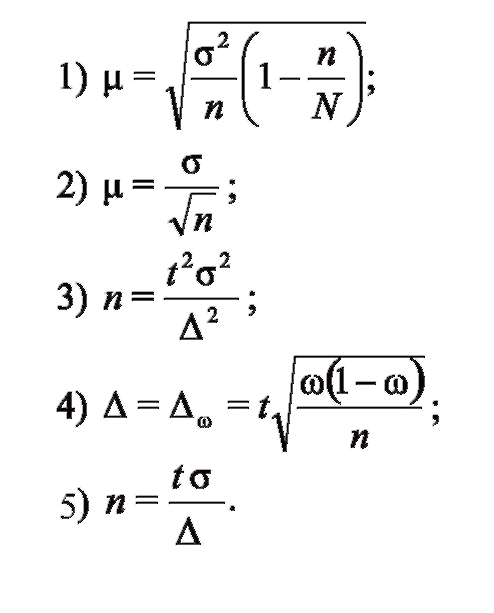
МОДУЛЬ 1.5.

1. Доверительными границами средних и относительных величин называют:

1) границы средних или относительных величин, выход за пределы которых вследствие случайных колебаний имеет незначительную вероятность;

2) границы средних и относительных величин, выход за пределы которых имеет большую вероятность;

3) пределы, в которых может быть любая величина выборочной совокупности;

4) пределы, в которых не может быть искомой величины генеральной совокупности;

5) статистическое распределение случайной величины.

2. По какой формуле можно рассчитать среднюю ошибку относительной величины?

ОТВЕТ 3

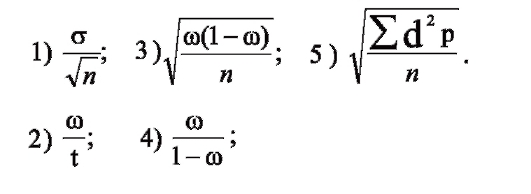
3. Назовите все условия, определяющие достоверность результатов исследования:

1) разнообразие признака в статистической совокупности, надежность;

2) разнообразие признака в статистической совокупности, число наблюдений, надежность;

3) число наблюдений, надежность, доверительные границы;

4) надежность, доверительные границы, критерий соответствия;

5) число наблюдений, разнообразие признака в статистической совокупности, доверительные границы.

4. По какой формуле можно рассчитать среднюю ошибку при оценке математического ожидания?

ОТВЕТ 4

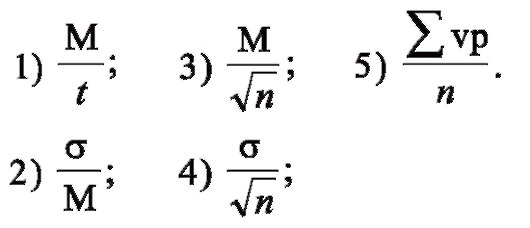
5. Какое значение доверительной вероятности чаще всего используется в медико-биологических исследованиях?

1) 0,68;

2) 0,75;

3) 0,80;

4) 0,95;

5) 0,85.

6. По какой формуле рассчитываются доверительные границы для средних величин?

ОТВЕТ 2

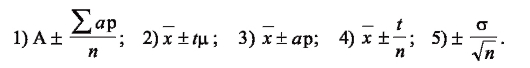
7. По какой формуле рассчитываются доверительные границы для вероятностей?

ОТВЕТ 3

8. При каком объеме единиц наблюдения выборка считается малой?

1) до 100;

2) до 70;

3) до 40;

4) до 30;

5) до 15.

9. Если критерий Стьюдента больше или равен 2, то различия двух средних величин:

1) незначимы;

2) значимы;

3) сравнимы;

4) несравнимы;

5) случайны.

10. Оценить достоверность результатов исследования означает:

1) определить, с какой надежностью возможно перенести результаты, полученные при выборочном исследовании на всю генеральную совокупность;

2) определить, с какой вероятностью возможно перенести результаты генеральной совокупности на выборочную;

3) сравнить результаты исследования с некими средними статистическими величинами;

4) оценить оптимальный объем выборки;

5) определить их достоверность искомым величинам.

11. По какой формуле можно рассчитать среднюю ошибку при оценке вероятности?

ОТВЕТ 3

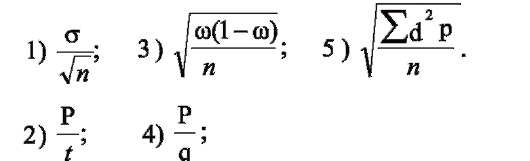
12. С помощью какой формулы определяется статистическая значимость различий между двумя средними (М₁ и М₂) или между двумя вероятностями (Р₁ и Р₂)?

ОТВЕТ 3

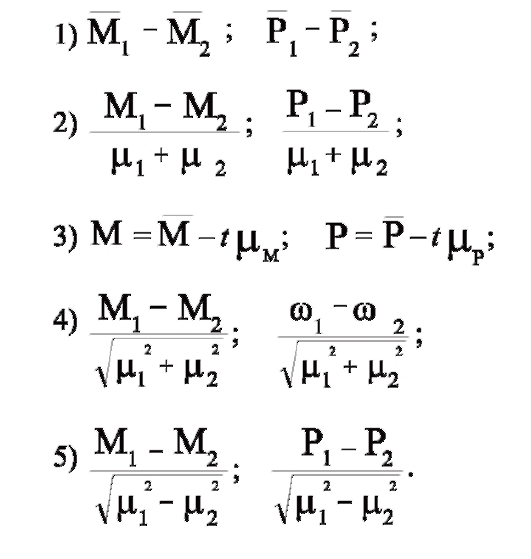
13. При каком значении Т с надежностью γ = 0,9544 можно утверждать, что между сравниваемыми величинами (средними или вероятностями) имеются существенные различия?

1) 1,0;

2) 1,5;

3) 2,0;

4) 2,5;

5) 3,0.

14. Если полученное при выборочном исследовании различие между сравниваемыми средними или вероятностями незначимо, то для увеличения надежности вывода следует:

1) использовать другие методы оценки достоверности;

2) увеличить число наблюдений;

3) использовать другие способы формирования выборочной совокупности;

4) изучить структуру генеральной совокупности;

5) провести априорный (разведочный) анализ данных.

МОДУЛЬ 1.6

1. В каких случаях применяются стандартизованные коэффициенты?

1) для определения существенных различий в интенсивных показателях;

2) сравнения относительных величин в неоднородных по составу совокупностях;

3) сравнения показателей рождаемости, смертности, заболеваемости в неоднородных по возрастному и половому составу совокупностях;

4) изучения влияния какого-либо фактора на интенсивные показатели сравниваемых совокупностей;

5) сравнительного анализа средних величин.

2. Условные гипотетические величины, используемые для анализа неоднородных совокупностей, - это:

1) коэффициент регрессии;

2) статистический критерий Стьюдента;

3) коэффициент корреляции;

4) стандартизованный коэффициент;

5) средние величины.

3. Назовите методы вычисления стандартизованных коэффициентов:

1) прямой, косвенный, обратный;

2) прямой, обратный, дискретный;

3) косвенный, дискретный, непрямой;

4) обратный, косвенный, непрямой;

5) прямой, непрямой, обратный.

4. Перечислите этапы для расчета стандартизованных коэффициентов:

1) выбор стандарта; вычисление интенсивных показателей; расчет стандартизованных коэффициентов; сопоставление и анализ полученных показателей;

2) вычисление интенсивных показателей; выбор стандарта; расчет стандартизованных коэффициентов; определение причин несоответствия полученных показателей;

3) выбор стандарта; расчет стандартизованных коэффициентов; вычисление интенсивных показателей;

4) изучение структуры совокупностей; вычисление интенсивных показателей; выбор стандарта; расчет стандартизованных коэффициентов;

5) вычисление интенсивных показателей; выбор стандарта; расчет стандартизованных коэффициентов.

5. При анализе каких показателей общественного здоровья наиболее часто возникает необходимость расчета стандартизованных коэффициентов?

1) физического здоровья;

2) медико-демографических процессов;

3) инвалидности;

4) социальной обусловленности здоровья;

5) всех перечисленных.

6. Какие различия определяются стандартизованными коэффициентами?

1) уровень доходов населения;

2) численность населения;

3) число случаев смерти;

4) возрастно-половой состав;

5) по числу случаев рождений.

7. Какие коэффициенты используются для сравнительного анализа уровней смертности в неоднородных по возрастно-половому составу совокупностях?

1) коэффициенты корреляции;

2) коэффициенты регрессии;

3) стандартизованные коэффициенты;

4) общий коэффициент смертности;

5) коэффициент младенческой смертности.

МОДУЛЬ 1.7.

1. Дайте определение временного (динамического) ряда:

1) научно обоснованное предположение о поведении показателя в определенный момент времени;

2) последовательность числовых значений статистического показателя, записанных в хронологическом порядке;

3) числовые значения статистического показателя;

4) последовательность результатов воздействия определенно направленных факторов;

5) результат действия множества факторов, имеющих случайный характер.

2. Как называются численные значения статистического показателя временного ряда?

1) прогностические значения;

2) тренды;

3) уровни ряда;

4) случайные составляющие;

5) закономерные составляющие.

3. Характеристика, выражающая основную тенденцию изменения уровней ряда, - это:

1) случайная составляющая;

2) закономерная составляющая;

3) прогноз;

4) средняя величина;

5) тренд.

4. Дайте определение закономерной составляющей временного ряда:

1) числовые значения статистического показателя;

2) последовательность числовых значений статистического показателя, записанных в хронологическом порядке;

3) научно обоснованное предположение о поведении показателя в определенный момент времени;

4) результат воздействия долговременных определенно направленных факторов;

5) результат действия множества факторов, имеющих случайный характер.

5. Какими величинами может быть представлен временной ряд?

1) абсолютными, относительными, средними;

2) только абсолютными;

3) только относительными;

4) абсолютными, средними, дискретными случайными;

5) средними, относительными, дискретными случайными.

6. Назовите типы временных рядов:

1) интервальные, относительные;

2) моментные, интервальные;

3) моментные, абсолютные;

4) моментные, средние;

5) абсолютные, интервальные.

7. По формуле ∆i_j = y_j - y_i; определяется:

1) темп прироста;

2) коэффициент роста;

3) значение 1% прироста;

4) абсолютный прирост;

5) темп роста.

8. Какие бывают виды абсолютного прироста?

1) базисные, абсолютные;

2) абсолютные, относительные;

3) базисные, цепные;

4) относительные, средние;

5) средние, цепные.

9. По формуле Т_пр% = Т_р% - 100% определяется:

1) темп роста;

2) абсолютный прирост;

3) значение 1% прироста;

4) средний темп прироста;

5) темп прироста.

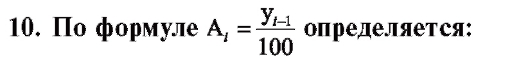
1) коэффициент опережения;

2) пункт роста;

3) средний темп прироста;

4) абсолютное значение 1% прироста;

5) темп роста.

МОДУЛЬ 1.8.

1. Дайте определение стохастической зависимости:

1) изменение одной случайной величины приводит к изменению закона распределения другой;

2) изменение двух случайных величин приведет к изменению одной из них;

3) изменение одной случайной величины не всегда приводит к изменению другой величины;

4) изменение одной из случайных величин приводит к изменению среднего другой случайной величины.

5) изменение двух случайных величин приведет к изменению третьей величины.

2. Если изменение одной из случайных величин приводит к изменению среднего другой случайной величины, то стохастическую зависимость называют:

1) случайной;

2) линейной;

3) достоверной;

4) корреляционной;

5) функциональной.

3. Назовите непараметрические методы оценки корреляционной зависимости:

1) критерий Колмогорова-Смирнова; коэффициент контингенции Пирсона;

2) коэффициент регрессии; критерий соответствия;

3) коэффициент ассоциации Юла; коэффициент контингенции Пирсона;

4) коэффициент ассоциации Юла; критерий соответствия;

5) коэффициент контингенции Пирсона; критерий Вилкоксона.

4. Укажите значения, которые может принимать коэффициент ассоциации:

1) от 0 до +1;

2) от -2 до +2;

3) от -1 до 0;

4) от -1 до +1;

5) от -1,5 до +1,5.

5. Какое значение имеет шкала Чеддока?

1) позволяет дать качественную оценку силы связи согласно коэффициентам ассоциации Юла и контингенции Пирсона, а также коэффициента корреляции пирсона;