
лекции / лекция 2 ММОСУ
.pdfЛекция 2. Системы линейных алгебраических уравнений
2.1 Решение систем линейных алгебраических уравнений
2.1.1 Определения и основные свойства матриц
Для начала напомним некоторые сведения из линейной алгебры. Рассмотрим систему из n линейных алгебраических уравнений (СЛАУ) с
n неизвестными x1, ,xn :
a11x1 a12x2 a1nxn b1, |
|
|
|
|
|
||||||||||||||
|
|
|
|
a22x2 a2nxn b2, |
|
|
|
|
|
||||||||||
a21x2 |
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
n1 |
a |
n2 |
x |
2 |
a |
nn |
x |
n |
b . |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|||||
Запишем СЛАУ в матричной форме, для этого введем векторы |
|||||||||||||||||||
|
x |
|
|
|
b |
|
|
|
|
|
a |
|
a |
|
|||||
|
|
|
1 |
|
|
|
1 |
|
|
|
|
|
|
11 |
|
1n |
|||
x |
,b |
|
и матрицу A |
|
|
|
. |
||||||||||||
|
x |
n |
|
|
|
b |
|
|
|
|
|
a |
n1 |
a |
|
|
|||
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
nn |
|||||
Тогда СЛАУ примет вид |
|
|
|
|
|
||||||||||||||
Ax b. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Определение: A 1 |
– обратная матрица для квадратной матрицы А, если |
||||||||||||||||||
AA 1 I , где I |
– единичная матрица. |
|
|
|
|
|
|||||||||||||
Определение: А — невырожденная, если для А существует A 1. Теорема: следующие утверждения эквивалентны:
1.А — невырождена;
2.det A 0;
3.линейная однородная система Ax 0 имеет единственное решение
x0;
4.для любого b система Ax b имеет единственное решение;
5.столбцы (строки) матрицы А линейно независимы, то есть для любой
комбинации чисел 1, 2, n , не все из которых равны нулю, линейная комбинация

|
a11 |
|
|
|
a12 |
|
|
|
a1n |
|
|
|
0 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a21 |
|
|
|
a22 |
|
|
|
a2n |
|
|
|
0 |
|
|
|||
|
|
|
2 |
|
|
|
n |
|
|
|
|
|
|
|
||||
1 |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
an1 |
|
|
|
an2 |
|
|
|
ann |
|
|
|
|
|
||||
Определение: ранг матрицы – |
|
rank(A) – число линейно независимых |
||||||||||||||||
столбцов (строк). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Следствие: А — невырожденная, если и только если А — полного ранга |
||||||||||||||||||
(rank(A)=n). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Определение: комплексное или вещественное число и вектор |
x 0, |
|||||||||||||||||
x Rn |
|
называются |
собственным |
значением и собственным вектором |
||||||||||||||
матрицы А, если они удовлетворяют алгебраическому уравнению
Ax x
Собственный вектор — это такой вектор, который, будучи умножен на матрицу А, изменяет лишь свою длину.
Из определения собственного значения следует:
Ax x 0 A I x 0.
Так как x — собственный вектор и по определению x 0, то в соответствии с теоремой A I — вырожденная матрица, а det A I 0.
Левая часть последнего выражения — полином степени n относительно комплексной переменной , называемый характеристическим полиномом матрицы, следовательно собственные значения матрицы есть корни характеристического полинома матрицы A, их ровно n с учетом кратности.
Определение: совокупность всех собственных значений i in 1 матрицы
А называется спектром матрицы А, а величина
A max i
1 i n
называется спектральным радиусом. Определение: нормой матрицы А называется
A |
|
|
|
sup |
|
|
Ax |
|
|
AT A1 2. |
||
|
|
|
|
|
|
|||||||
|
|
|||||||||||
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
x |
|
|
|
|||
|
|
|
|
|
|
|
||||||
|
|
|
|
x Rn |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
||
Решение СЛАУ методом исключения
Одной из наиболее распространенных задач является задача решения СЛАУ
Ax b,
для заданных квадратной матрицы А и вектора b.
Если А — невырожденная матрица, то для нее существует обратная A 1.
Умножая СЛАУ на A 1 слева, получим решение: x A 1b.
Полученный метод решения СЛАУ неэффективен в силу большого времени вычислений.
Рассмотрим более эффективный алгоритм решения СЛАУ – метод исключения Гаусса. Этот алгоритм с некоторыми модификациями используют для решения СЛАУ до двухсотого порядка.
Вначале продемонстрируем работу алгоритма на примере следующей СЛАУ:
4x1 9x2 2x3 6, |
|
|
|
|
|||||||
|
|
|
4x3 6, |
|
|
|
|
||||
2x1 4x2 |
|
|
|
|
|||||||
x 2x |
2 |
2x 1, |
|
|
|
||||||
|
1 |
|
3 |
|
|
|
|
|
|||
которую запишем в матричной форме |
|
||||||||||
4 |
9 |
|
2 x1 |
|
|
6 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
4 |
|
4 |
x2 |
|
|
6 |
. |
|
|
|
1 2 |
|
2 |
x |
3 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Введем расширенную матрицу системы: |
|
||||||||||
|
4 |
9 |
|
2 |
6 |
|
|
|
|
|
|
|
2 |
4 |
|
4 |
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
1 |
2 |
|
2 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
На |
первом |
шаге |
алгоритма исключим x1 из второго |
и третьего |
|||||||
уравнений системы. |
Для исключения x1 во втором уравнении, |
из второго |
|||||||||
уравнения вычтем первое, умноженное на l21 2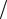 4. Для исключения x1 в
4. Для исключения x1 в
третьем уравнения из него вычтем первое, умноженное на l31 1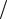 4. В результате после первого шага исключения получим
4. В результате после первого шага исключения получим
|
|
9 |
|
|
|
|
|
||
|
4 |
2 |
6 |
|
|||||
|
|
|
1 |
|
|
|
|
|
|
|
0 |
|
3 |
3 |
. |
||||
2 |
|
||||||||
|
|
|
|
|
|
|
|
||
|
0 |
1 |
|
5 |
|
5 |
|
||
|
|
|
|
|
|
|
|
|
|
4 |
|
2 |
|
2 |
|||||
|
|
|
|
|
|||||
На втором шаге алгоритма исключим x2 в третьем уравнении, для чего из третьего уравнения вычтем первое, умноженное на l32 1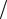 2. После второго шага исключения получим
2. После второго шага исключения получим
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
9 |
2 |
6 |
|
|
|
0 |
|
0 |
0 |
|
|||||
|
|
|
|
||||||||||||||
|
|
|
1 |
|
|
|
|
|
|
||||||||
|
0 |
|
3 3 |
|
, |
L |
|
1 |
|
0 |
0 |
. |
|||||
2 |
|
2 |
|
||||||||||||||
|
0 |
|
4 |
4 |
|
|
|
|
|
1 |
|
|
|||||
|
0 |
|
|
|
|
|
|
1 |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
4 |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|||
За два шага закончилась первая часть алгоритма — приведение системы к треугольной форме. Решение полученной треугольной системы осуществляется снизу вверх
x3 44 1;
x2 2 3 3x3 0;
x1 14 6 2x3 9x2 1.
Перейдем к построению алгоритма исключения для СЛАУ общего вида
a11x1 a12x2 a1nxn b1, |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
a21x2 a22x2 a2nxn b2, |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
n1 |
a |
n2 |
x |
2 |
a |
nn |
x |
n |
b . |
|
|
|
|
|
n |
|||||
Шаг 1: исключим x1 из уравнений с номерами 2,…, n путем вычитания:
из второго уравнения первого, умноженного на l21 a21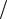 a11 ;
a11 ;

…
из n-ого уравнения первого, умноженного на ln1 an1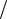 a11 . После первого шага система уравнений преобразуется к виду
a11 . После первого шага система уравнений преобразуется к виду
|
a11x1 a12x2 a1nxn b1, |
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
a 1 x |
|
|
a |
1 x |
|
|
|
b 1 , |
|
|
|
|
|
||||||
|
|
|
|
2 |
n |
|
|
|
|
|
|
||||||||||||
|
|
|
22 |
|
|
|
|
2n |
|
2 |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a 1 x |
2 |
|
a 1 x |
n |
b 1 . |
|
|
|
|
|
|||||||||
|
|
|
|
n2 |
|
|
|
|
|
nn |
|
n |
|
|
|
|
|
|
|||||
где |
a 1 |
a |
ij |
l |
a |
|
|
,b 1 |
b l |
b ,l |
i1 |
a |
a ,i, j 2, ,n |
||||||||||
ij |
|
|
i1 |
1j |
i |
|
|
i |
|
|
i1 1 |
|
|
|
i1 |
11 |
|||||||
|
Шаг 2: исключим |
x2 |
из уравнений с номерами 3,…, n путем вычитания: |
||||||||||||||||||||
|
Из третьего уравнения второго, умноженного на l32 a32 a22 |
||||||||||||||||||||||
|
…. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Из n-ого уравнения второго‚ умноженного на ln2 an2 a22 . |
||||||||||||||||||||||
|
После второго шага получим |
|
|
|
|
|
|
|
|||||||||||||||
|
a11x1 a12x2 a13x3 a1nxn b1, |
|
|||||||||||||||||||||
|
|
|
|
a 1 x |
|
|
a |
1 x a 1 x |
|
|
b 1 , |
|
|||||||||||
|
|
|
|
2 |
n |
|
|||||||||||||||||
|
|
|
22 |
|
|
23 |
3 |
|
|
|
|
2n |
|
2 |
|
||||||||
|
|
|
|
|
|
|
|
|
a |
2 x a 2 x |
n |
b |
2 |
, |
|||||||||
|
|
|
|
|
|
|
|
|
33 |
3 |
|
|
|
|
3n |
|
|
3 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|
2 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xn |
|
|
|||||||
|
|
|
|
|
|
|
|
|
an3 x3 |
ann |
bn |
. |
|||||||||||
После n-1 шага исключения исходная система придет к треугольной
форме
a11 |
a12 |
|
|
0 |
a221 |
|
||
|
|
|
|
|
|
|
|
|
|
0 |
0 |
|
||
где
a1n |
x1 |
|
|
|
|
b1 |
|
||
1 |
|
|
|
|
|
|
|
1 |
|
a2n |
x2 |
|
|
|
b2 |
|
|||
|
|
|
|
|
|
|
|
||
|
|
|
|||||||
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
||||
a n 1 x |
n |
|
|
b |
n 1 |
||||
nn |
|
|
|
|
|
n |
|
||
a k 1
lik aikk 1 ,bik bik 1 likbkk 1 ,aijk aijk 1 likaijk 1 , kk
k=1,…n–1– номер шага исключения, i=k+1, …, n – номер строки, j=k+1, …, n - номер столбца.
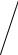
Решение треугольной системы осуществляется путем обратной подстановки k=n, n-1, …, 1.
|
|
|
n |
k 1 |
|
k 1 |
|
|
|
|
xk |
k-1 |
|
|
|
. |
|
|
|
||
bk |
akj |
xj |
akk |
|
|
|
||||
|
|
|
j k 1 |
|
|
|
|
|
|
|
При |
реализации |
алгоритма |
в виде программы элементы |
a k |
и |
b k |
||||
|
|
|
|
|
|
|
|
ij |
|
i |
обычно хранят на месте исходных элементов aij , bi , поэтому их прежние значения будут изменены. Приведем программу, реализующую алгоритм решения СЛАУ методом исключения.
LU-факторизация матриц
Впроцессе исключения по Гауссу исходная матрица СЛАУ А приведена
кверхней треугольной матрице
u11 |
u12 |
u1n |
|
|
|
|
u22 |
|
|
|
0 |
u2n |
|
|
U |
|
|
|
, |
|
|
|
|
|
|
|
|
||
|
0 |
0 |
|
|
|
unn |
|
||
где элементы матрицы, расположенные ниже главной диагонали, равны нулю. Введем в рассмотрение нижнюю треугольную матрицу, на главной диагонали которой расположены единицы, а под главной диагональю помещены lij, полученные в процессе приведения А к верхнетреугольному виду
1 |
0 |
|
0 |
|
|
|
|
|
|
|
|
l21 |
1 |
|
0 |
|
|
L |
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
||
|
|
ln2 |
|
1 |
|
ln1 |
|
||||
Можно показать, что
A LU ,
то есть в процессе решения СЛАУ с использованием метода исключения получено разложение (факторизация) исходной матрицы на нижнетреугольную с единичной главной диагональю и верхнетреугольную.
Если проведена LU-факторизация матрицы СЛАУ Ax b, то решение системы может быть получено следующим образом. Исходную систему перепишем в виде
LUx b.
Введем обозначение Ux y, тогда исходная система сведется к двум СЛАУ
Ly b, Ux y,
каждая из которых проще, чем исходная, так как имеет треутольную матрицу.
Решение первой системы -
1 |
|
0 |
0 y1 |
|
|
b1 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
l21 |
|
1 |
0 |
y2 |
|
|
b2 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
||||
|
l |
|
1 |
|
|
|
|
|||||
l |
n1 |
n2 |
y |
n |
|
|
b |
|
||||
|
|
|
|
|
|
|
|
n |
|
|||
легко вычисляется прямой подстановкой
y1 b1,
y2 b2 l21y1,
yn bn ln1y1 ln,n 1yn 1,
или, в общем виде:
k 1
yk bk lki yi i 1
После того как получен вектор у, можно решить вторую треугольную систему

u11 |
u12 |
u1n x1 |
|
|
y1 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
0 |
u22 u2n x2 |
|
|
y2 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|||
|
|
|
|
|
|||||
|
0 |
0 |
|
|
|
|
|
|
|
|
unn xn |
|
|
yn |
|
||||
путем обратной подстановки
xn u1nn yn ,
xn 1 |
|
|
1 |
|
yn 1 un 1,nxn , |
|
|
|
|
||||
|
|
un 1,n 1 |
|
|||
… |
|
|
|
|
|
|
|
1 |
|
|
|
n |
|
|
|
|
|
|
|
|
x1 u |
|
y1 |
u1jxj . |
|||
|
11 |
|
j 2 |
|
||
или, в общем виде:
xk u1kk yk j nk u1kjxj , k n,n 1, ,1.
Таким образом, применение LU-факторизации сводит решение исходной СЛАУ к последовательному решению двух СЛАУ c треугольными матрицами. Если требуется решить несколько СЛАУ о одной и той же матрицей А и различными правыми частями
Ax b ; x |
,b Rn, |
i 1, ,n, |
i i i |
i |
|
то предварительная LU-факторизация матрицы системы А позволяет существенно сократить трудоемкость решения n систем, сводя задачу к решению 2n СЛАУ с треугольными матрицами
Lyi bi ,
Uxi yi .
Вычисление определителя и обратной матрицы
Определитель матрицы А является побочным продуктом LU-факторизации матрицы А, действительно:
det A det LU det L det U .
Второе равенство получено на основании того, что определитель произведения матриц равен произведению определителей сомножителей.
Вычислим определитель каждого из сомножителей. Определитель треугольной матрицы равен произведению диагональных элементов,
|
|
1 |
0 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l21 |
1 |
|
0 |
|
1, |
|
|
|
|
|
||
det |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
ln2 |
|
1 |
|
|
|
|
|
|
|
|
|
ln1 |
|
|
|
|
|
|
|
|
||||
|
u11 |
u12 |
u1n |
|
|
|
|
|
|
||||
|
|
|
u22 |
|
|
|
|
|
|
|
|
|
|
det |
|
0 |
u2n |
u |
u |
|
u |
|
, |
||||
|
|
|
|
|
|
|
22 |
nn |
|||||
|
|
|
|
|
|
11 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
unn |
|
|
|
|
|
|
|||||
следовательно
det A in 1uii .
В MATLAB реализована функция вычисления определителя матрицы
D = det(A).
Перейдем к рассмотрению вопроса о вычислений обратной матрицы. По определению обратная матрица X удовлетворяет матричному алгебраическому уравнению
AX I
Представим матрицы X и I в виде наборов их столбцов
X x | x |
2 |
| | x |
n |
; |
x |
Rn; |
|||
1 |
|
|
|
|
|
i |
|
||
I e |e |
2 |
| |e |
n |
; |
|
e Rn; |
|||
1 |
|
|
|
|
|
i |
|
||
где ei – вектор, который имеет все нулевые элементы за исключением i-ого, равного 1. Тогда матричное уравнение для обратной матрицы можно переписать в виде
A x1 | x2 | | xn e1 |e2 | |en ,
то есть представляет собой n СЛАУ вида
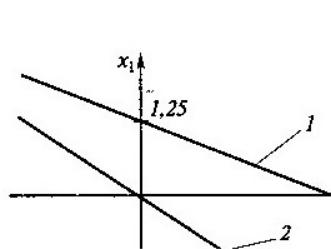
Axi ei, i 1, ,n.
Таким образом, для вычисления обратной матрицы необходимо решить n СЛАУ и составить из полученных решений матрицу. Учитывая, что все n СЛАУ имеют одинаковую матрицу А, целесообразно произвести ее LUфакторизацию и свести задачу вычисления обратной матрицы к решению 2n СЛАУ с треугольными матрицами
Lyi ei, |
|
Uxi yi, |
i 1, ,n. |
Обусловленность СЛАУ. Анализ ошибок решения СЛАУ
Определение: СЛАУ плохо обусловлена, если малые изменения элементов матрицы А или вектора b приводят к большим изменениям в решении.
Рассмотрим пример плохо обусловленной СЛАУ:
0,8x1 0,4x2 1, 0,79x1 0,41x2 .
Решения этой системы x0 для 0 и x для малого значения будут сильно отличаться. Это связано с тем, что на плоскости x1x2 уравнения системы задают “почти” параллельные прямые 1 и 2 (рис. 2.1). Следовательно, уравнения являются “почти” линейнозависимыми, и при их малом изменении относительно друг друга точка пересечения прямых будет значительно меняться.
