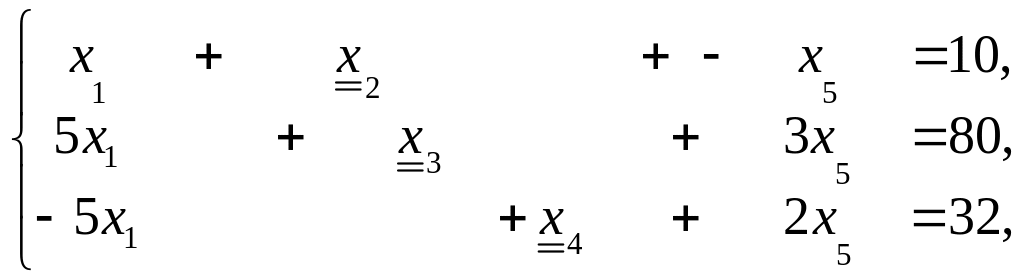- •Оглавление
- •1. Предмет математического программирования. Линейное программирование
- •1.1. Введение. Предмет математического программирования
- •1.2. Линейное программирование. Общие понятия
- •1.3. Построение математических моделей простейших экономических задач
- •1.4. Замена неравенств уравнениями
- •1.5. Основные виды записи задач линейного программирования
- •Задание для самостоятельной работы
- •2. Графическое решение задачи линейного программирования
- •2.1. Свойства решений задач линейного программирования
- •2.2. Основные случаи графического решения задач линейного программирования
- •Задания для самостоятельной работы
- •3. Симплексный метод решения задач линейного программирования
- •3.1. Построение начального опорного плана
- •3.2. Симплексные таблицы. Признак оптимальности опорного плана
- •3.3. Переход к нехудшему опорному плану
- •1 Итерация:
- •Задания для самостоятельной работы
- •4. Двойственность в линейном программировании
- •4.1. Понятие двойственности
- •4.2. Двойственный симплексный метод
- •Задания для самостоятельной работы
- •5. Элементы теории матричных игр
- •5.1. Матричные игры с нулевой суммой
- •5.2. Максиминные и минимаксные стратегии игроков
- •5.3. Чистые и смешанные стратегии и их свойства
- •5.4. Приведение матричной игры к задаче линейного программирования
- •1 Стр доминирует над 3 стр
- •Задание для самостоятельной работы
- •6. Транспортная задача линейного программирования
- •6.1. Постановка транспортной задачи и ее математическая модель
- •6.2. Закрытая и открытая модели транспортной задачи
- •6.3. Построение исходного опорного плана
- •1. Метод северо-западного угла
- •2. Метод «минимального элемента»
- •6.4. Метод потенциалов решения транспортной задачи, признак оптимальности опорных планов
- •6.5. Решение транспортной задачи с открытой моделью
- •Задания для самостоятельной работы
- •7. Элементы сетевого планирования
- •7.1. Основные понятия
- •7.2. Временные параметры сети (рассмотрим на примере)
- •Задания для самостоятельной работы
- •8. Решение задач линейного программирования с использованием эвм
- •Задание для самостоятельной работы
- •Список используемой литературы
- •400005, Г. Волгоград, просп. Им. В. И. Ленина, 28, корп. 1.
- •403874, Г. Камышин, ул. Ленина, 5.
3.1. Построение начального опорного плана
1.
Пусть задача линейного программирования
представлена целевой функцией Z=c1х1
+с2х2
+...+сnхn
=
![]() сjхj
и системой ограничений, заданной в
каноническом виде
сjхj
и системой ограничений, заданной в
каноническом виде
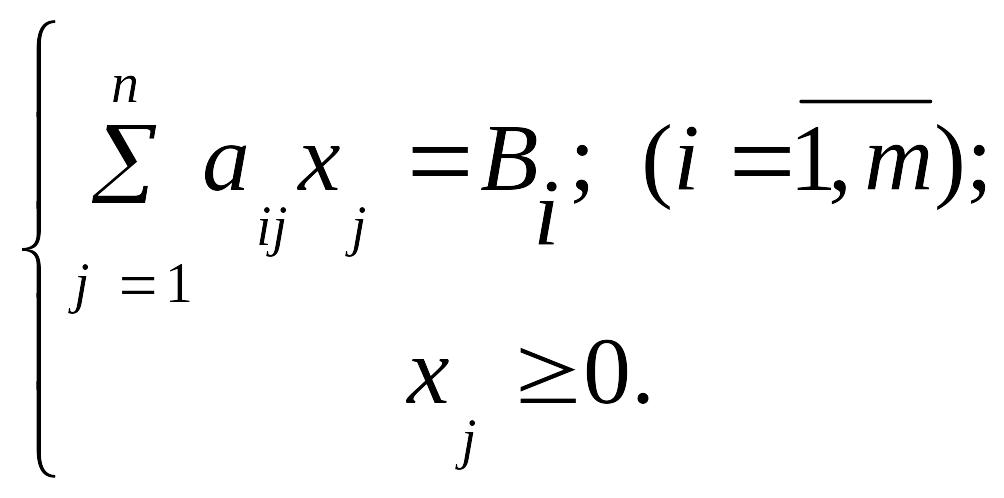
Говорят, что ограничение задачи линейного программирования имеет предпочтительный вид, если вi 0 и левая часть этого ограничения содержит переменную с коэффициентом 1, а в остальные ограничения – равенства она входит с коэффициентом равным 0.
Пример
7.

Первое и второе ограничения имеют предпочтительный вид, а третье – нет.
Если каждое ограничение – равенство задачи линейного программирования имеет предпочтительный вид, то и система ограничений представлена в предпочтительном виде. В этом случае легко найти ее опорное решение: все свободные переменные приравниваются к нулю, тогда базисные переменные равны свободным членам.
Пример 8.
|
|
а)
предпочтительными, т. е. базисными
переменными являются х2,
х3,
х4,
а свободными – х1
и х5
х1
= 0, х5
= 0, а х2
= 10, х3
= 0, х4
= 2. Тогда начальный опорный план
![]() =(0;
10; 80; 32; 0) –
угловая точка (согласно теореме 1).
=(0;
10; 80; 32; 0) –
угловая точка (согласно теореме 1).
б)
пусть
система ограничений имеет вид
![]() вi;
вi
0 (i
=
вi;
вi
0 (i
=
![]() )
в задаче линейного программирования
на max (задача об использовании сырья).
Сведем задачу к каноническому виду, для
этого добавим к левым частям неравенств
дополнительные переменные хn
+ i
0 (i
=
),
тогда получим систему равенств
)
в задаче линейного программирования
на max (задача об использовании сырья).
Сведем задачу к каноническому виду, для
этого добавим к левым частям неравенств
дополнительные переменные хn
+ i
0 (i
=
),
тогда получим систему равенств
![]() вi;
вi
0 (i
=
),
которая
будет
иметь предпочтительный вид и, следовательно,
начальный опорный план будет
вi;
вi
0 (i
=
),
которая
будет
иметь предпочтительный вид и, следовательно,
начальный опорный план будет
![]() =
(0,...0, в1,
в2,…,
вm)
(так как в этой системе все дополнительные
переменные будут базисными, а в целевую
функцию дополнительные переменные
входят с коэффициентом равным 0), то Z
= c1x1
+ c2x2
+ … cnxn
+ 0xn+1
+ …0xn+m.
=
(0,...0, в1,
в2,…,
вm)
(так как в этой системе все дополнительные
переменные будут базисными, а в целевую
функцию дополнительные переменные
входят с коэффициентом равным 0), то Z
= c1x1
+ c2x2
+ … cnxn
+ 0xn+1
+ …0xn+m.
в)
в задачах линейного программирования
на min (задача о составлении рациона)
система ограничений имеет вид
![]() вi;
вi
0, (i
=
).
Если мы сведем эту задачу к каноническому
виду, то надо из каждого неравенства
(из левой части) вычесть дополнительные
переменные хn+i
0 (i
=
).
Получим систему
вi;
вi
0, (i
=
).
Если мы сведем эту задачу к каноническому
виду, то надо из каждого неравенства
(из левой части) вычесть дополнительные
переменные хn+i
0 (i
=
).
Получим систему
![]() вi;
вi
0, (i
=
),
однако теперь система ограничений не
имеет предпочтительного вида, так как
дополнительные переменные хn
+ i
входят в левую часть с коэффициентами
(–
1). В этом случае вводится так называемый
искусственный базис: к левым частям
ограничений равенств, не имеющих
предпочтительного вида, добавляют
искусственные переменные i.
вi;
вi
0, (i
=
),
однако теперь система ограничений не
имеет предпочтительного вида, так как
дополнительные переменные хn
+ i
входят в левую часть с коэффициентами
(–
1). В этом случае вводится так называемый
искусственный базис: к левым частям
ограничений равенств, не имеющих
предпочтительного вида, добавляют
искусственные переменные i.
В целевую функцию переменные i вводят с коэффициентом М в случае решения задачи на min и с коэффициентом (– M) для задачи на max, где М – большое положительное число. Полученная задача называется М-задачей, которая соответствует исходной. Она всегда имеет предпочтительный вид.
Пусть исходная задача линейного программирования имеет вид:
max(min)
Z
=
![]() ,
,
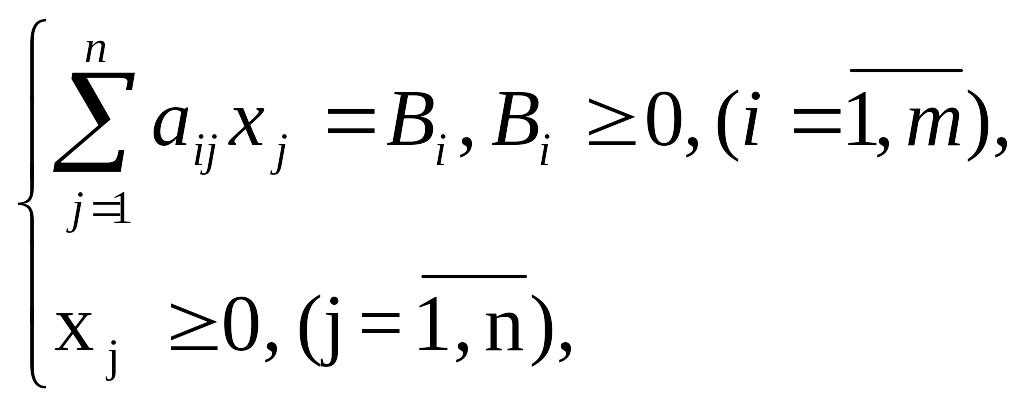
причем ни одно из ограничений не имеет предпочтительной переменной. Тогда М-задача запишется так:
max
(min)
=
![]() –
(+)
–
(+)![]() ,
,
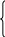
![]() вi
,(i
=
),
вi
,(i
=
),
хj
0, (j
=![]() ),
i
0 , (i
=
).
),
i
0 , (i
=
).
Эта
система ограничений имеет предпочтительный
вид, ее начальный опорный план
![]() = (0,...0, в1,
в2,
…, вm).
Если некоторые из уравнений исходной
системы ограничений имеют предпочтительный
вид, то в них не следует вводить
искусственные переменные. Итак, если в
оптимальном плане
= (0,...0, в1,
в2,
…, вm).
Если некоторые из уравнений исходной
системы ограничений имеют предпочтительный
вид, то в них не следует вводить
искусственные переменные. Итак, если в
оптимальном плане
![]() = (х1,
x2,
.., xn,
1,
2,
.., m)
М-задачи все искусственные переменные
I
= 0 (i
=
),
то план
=
(х1,
x2,
.., хn)
является оптимальным планом исходной
задачи. Можно сказать, что если в
результате применения симплексного
метода к М-задаче получен оптимальный
план, в котором все искусственные
переменные I
= 0, то его первые n-компоненты дают
оптимальный план исходной задачи. Если
же в оптимальном плане М-задачи хотя бы
одна из i
0, то исходная задача не имеет допустимых
планов, т. е. ее условия не совместны.
= (х1,
x2,
.., xn,
1,
2,
.., m)
М-задачи все искусственные переменные
I
= 0 (i
=
),
то план
=
(х1,
x2,
.., хn)
является оптимальным планом исходной
задачи. Можно сказать, что если в
результате применения симплексного
метода к М-задаче получен оптимальный
план, в котором все искусственные
переменные I
= 0, то его первые n-компоненты дают
оптимальный план исходной задачи. Если
же в оптимальном плане М-задачи хотя бы
одна из i
0, то исходная задача не имеет допустимых
планов, т. е. ее условия не совместны.