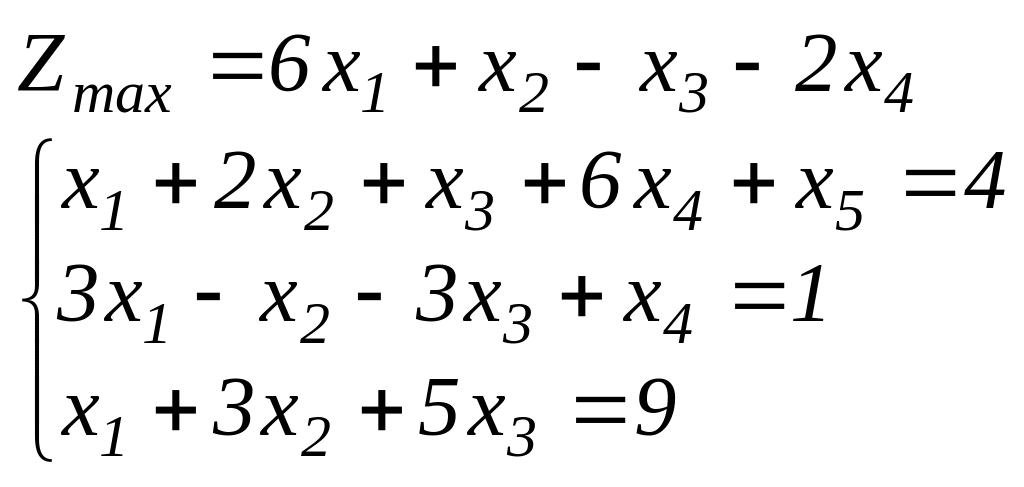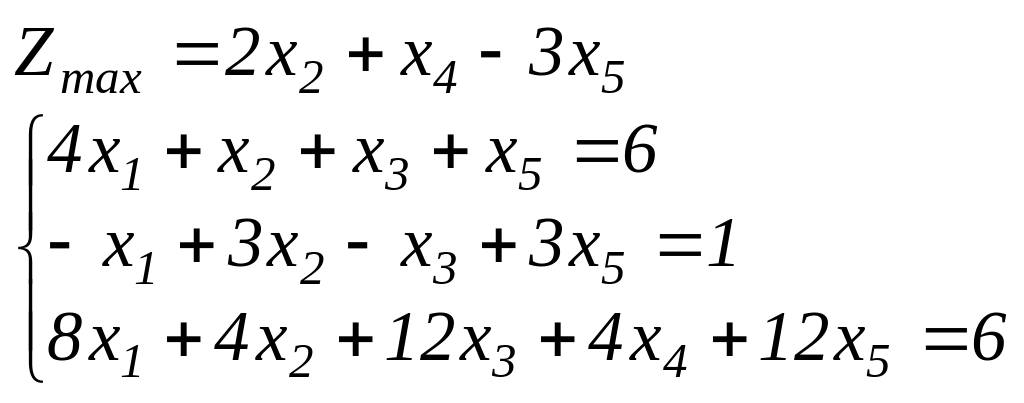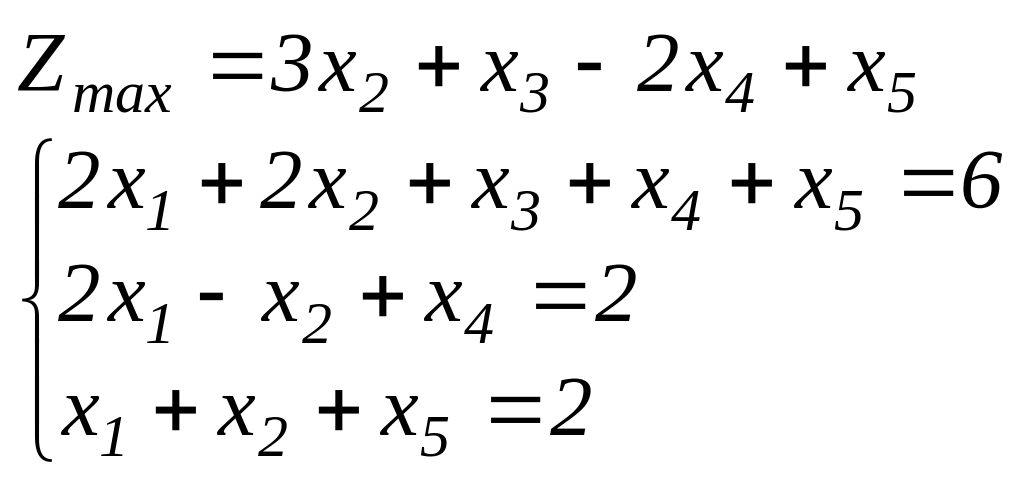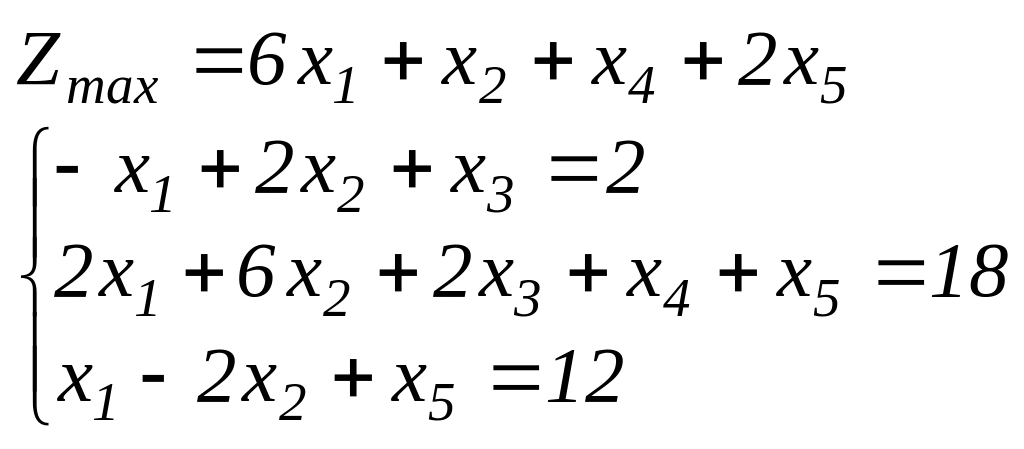- •Оглавление
- •1. Предмет математического программирования. Линейное программирование
- •1.1. Введение. Предмет математического программирования
- •1.2. Линейное программирование. Общие понятия
- •1.3. Построение математических моделей простейших экономических задач
- •1.4. Замена неравенств уравнениями
- •1.5. Основные виды записи задач линейного программирования
- •Задание для самостоятельной работы
- •2. Графическое решение задачи линейного программирования
- •2.1. Свойства решений задач линейного программирования
- •2.2. Основные случаи графического решения задач линейного программирования
- •Задания для самостоятельной работы
- •3. Симплексный метод решения задач линейного программирования
- •3.1. Построение начального опорного плана
- •3.2. Симплексные таблицы. Признак оптимальности опорного плана
- •3.3. Переход к нехудшему опорному плану
- •1 Итерация:
- •Задания для самостоятельной работы
- •4. Двойственность в линейном программировании
- •4.1. Понятие двойственности
- •4.2. Двойственный симплексный метод
- •Задания для самостоятельной работы
- •5. Элементы теории матричных игр
- •5.1. Матричные игры с нулевой суммой
- •5.2. Максиминные и минимаксные стратегии игроков
- •5.3. Чистые и смешанные стратегии и их свойства
- •5.4. Приведение матричной игры к задаче линейного программирования
- •1 Стр доминирует над 3 стр
- •Задание для самостоятельной работы
- •6. Транспортная задача линейного программирования
- •6.1. Постановка транспортной задачи и ее математическая модель
- •6.2. Закрытая и открытая модели транспортной задачи
- •6.3. Построение исходного опорного плана
- •1. Метод северо-западного угла
- •2. Метод «минимального элемента»
- •6.4. Метод потенциалов решения транспортной задачи, признак оптимальности опорных планов
- •6.5. Решение транспортной задачи с открытой моделью
- •Задания для самостоятельной работы
- •7. Элементы сетевого планирования
- •7.1. Основные понятия
- •7.2. Временные параметры сети (рассмотрим на примере)
- •Задания для самостоятельной работы
- •8. Решение задач линейного программирования с использованием эвм
- •Задание для самостоятельной работы
- •Список используемой литературы
- •400005, Г. Волгоград, просп. Им. В. И. Ленина, 28, корп. 1.
- •403874, Г. Камышин, ул. Ленина, 5.
Задания для самостоятельной работы
Задание 1. Решите графическим методом задачу линейного программирования (x1 ≥ 0, x2 ≥ 0):
1. |
|
6. |
|
11. |
|
|||||
2. |
|
7. |
|
12. |
|
|||||
3. |
|
8. |
|
13. |
|
|||||
4. |
|
9. |
|
14. |
|
|||||
5. |
|
10. |
|
15. |
|
|||||
16. |
|
21. |
|
26. |
|
|||||
17. |
|
22. |
|
27. |
|
|||||
18. |
|
23. |
|
28. |
|
|||||
19. |
|
24. |
|
29. |
|
|||||
20. |
|
25. |
|
30. |
|
|||||
Задание 2. Найти графическим методом оптимальный план задач линейного программирования (хj 0).
1. |
|
8. |
|
2. |
|
9. |
|
3. |
|
10. |
|
4. |
|
11. |
|
5. |
|
12. |
|
6. |
|
13. |
|
7. |
|
14. |
|
15. |
|
23. |
|
16. |
|
24. |
|
17. |
|
25. |
|
18. |
|
26. |
|
19. |
|
27. |
|
20 |
|
28. |
|
21 |
|
29. |
|
22. |
|
30. |
|
3. Симплексный метод решения задач линейного программирования
Доказано,
что оптимальное решение задачи линейного
программирования связано с угловыми
точками многогранника решений, поэтому
возникает мысль о следующем пути решения
задачи линейного программирования
с любым числом переменных. Найти
каким-нибудь способом все угловые точки
многогранника планов (а их
![]() =
=![]() ,
если каждый план определяется системой
m-линейно независимых векторов,
содержащихся в данной системе из n
векторов Ā1,
Ā2
,...,
Ān)
и сравнить в них значения целевой
функции. Но найти оптимальный план,
перебирая все опорные планы задачи
трудно, поэтому необходимо иметь схему,
позволяющую переходить к не худшему
опорному плану и иметь признак того,
что лучших крайних точек, чем данная
крайняя точка нет. В этом и состоит идея
наиболее широко применяемого в настоящее
время симплексного метода (метода
последовательного улучшения плана).
,
если каждый план определяется системой
m-линейно независимых векторов,
содержащихся в данной системе из n
векторов Ā1,
Ā2
,...,
Ān)
и сравнить в них значения целевой
функции. Но найти оптимальный план,
перебирая все опорные планы задачи
трудно, поэтому необходимо иметь схему,
позволяющую переходить к не худшему
опорному плану и иметь признак того,
что лучших крайних точек, чем данная
крайняя точка нет. В этом и состоит идея
наиболее широко применяемого в настоящее
время симплексного метода (метода
последовательного улучшения плана).
Итак, симплексный метод предполагает: умение находить начальный опорный план, наличие признака оптимальности (неоптимальности) опорного плана, умение переходить к нехудшему опорному плану.