1 Итерация:

1) выбираем разрешающий элемент из условия: max {|Δ₁|, |Δ₅|} = max (4; 1) = 4 – это соответствует 1 столбцу, поэтому его выбираем за разрешающий то есть X₁ будем вводить в базис. Для определения разрешающей строки находим минимальное симплексное отношение:

_{= =}

итак, 1 – строка разрешающая =>элемент а₁₁ = 1 – разрешающий;

2) переменную х₂ выведем из базиса, а х₁ введем в базис;

3) разрешающую строку делим на разрешающий элемент;

4) элементы разрешающего столбца заполняем нулями;

5) остальные элементы пересчитываем по правилу прямоугольника и делим на разрешающий элемент.

Делаем контрольные проверки:

14 – 5 + 216 – 1 40 = 62; 14 – 10 – 5 + 5 = 4;

14 + 0 + 0 – 14 = 0; 0 + 2 + 0 – 2 = 0;

0 + 0 – 1 + 1 = 0; – 14 + 16 + 1 – 8 = – 5 < 0.

Так как существует отрицательная оценка ∆₅ = – 5, план = (5; 0; 16; 40; 0) не оптимальный, Z(x₁) = 62 > Z ( ) = 42.

2 итерация:

1) разрешающий столбец 5, переменную. х₅ ,будем вводить в базис.

2) определяем разрешающую строку: min симплексное отношение _{= = 2 соответствует 2-ой строке, значит переменную х3} выводим из базиса. Разрешающий элемент а₂₅ = 8;

3) разрешающую строку делим на 8;

4) в разрешающем столбце проставляем нули;

5) остальные элементы пересчитываем;

6) делаем контрольные проверки, так же как и в итерации 1, так как все _j  0, опорный план – оптимален

Ответ: = (7; 0; 0; 42; 2), Z( ) = 72.

Пример 11. Решить М-задачу линейного программирования:

Найти: min Z = 3x₁ + 2х₂ + 3х₃, если

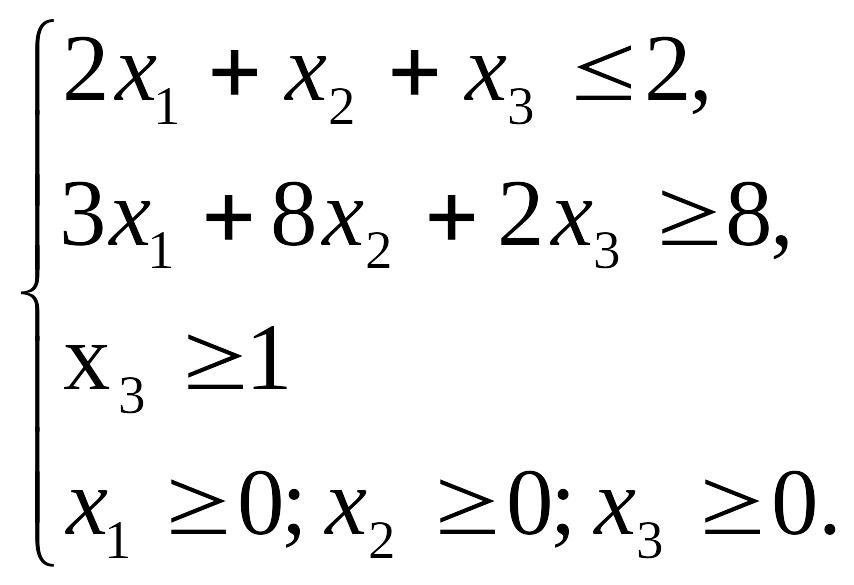
Решение:

Сведем задачу к каноническому виду и введем искусственные переменные и :

Занесем условие М-задачи в симплексную таблицу (индексную строку записываем в две строки: в первой – слагаемые без М, во второй – слагаемые с М) (табл. 20).

Таблица 20

№		БП	СБ		В	х1	х2	х3	х4	х5	х6	1	2	Q
						3	2	3	0	0	0	M	M
0		х4 1 2	0 М М		2 8 1	2 3 0	1 [8] 0	1 2 1	1 0 0	0 – 1 0	0 0 – 1	0 1 0	0 0 1	2/1 = 2 8/8 = [1]
					0	– 3	– 2	– 3	0	0	0	0	0
					9M	3M	[8M]	3M	0	– M	– M	0	0
1	х4 х2 2			0 2 М	1 1 1	13/8 3/8 0	0 1 0	3/4 1/4 [1]	1 0 0	1/8 – 1/8 0	0 0 – 1	– – –	0 0 1	1/ 1/ 1/1=[1]
					2	– 9/4	0	– 7/2	0	– 1/4	0	–	0
					М	0	0	[M]	0	0	-М	–	0

Окончание табл. 20

2	х4 х2 х3	0 2 3	1/4 3/4 1	13/8 3/8 0	0 1 0	0 0 1	1 0 0	1/8 – 1/8 0	3/4 1/4 – 1	– – –	– – –
			9/2	– 9/4	0	0	0	– 1/4	– 5/2

Примечание: по мере вывода из базиса искусственных переменных соответствующие им столбцы можно опускать.

Так как все _j ≤ 0, то план оптимален,

Ответ: = (0; 3/4; 1; 1/4; 0; 0), Z( ) = 9/2.

Замечания:

1. Если в индексной строке последней симплексной таблицы, содержащей оптимальный план, имеется хотя бы одна нулевая оценка, соответствующая свободной переменной, то задача линейного программирования имеет бесконечное множество оптимальных планов.

2. Если в индексной строке симплексной таблицы задачи линейного программирования на max содержится отрицательная оценка _j < 0, а в соответствующем столбце переменной х_j. нет ни одного положительного элемента, то целевая функция на множестве допустимых планов задачи не ограничена сверху.

Если же задача линейного программирования на min и в индексной строке содержится положительная оценка _j > 0, а в столбце переменной х_j нет ни одного положительного элемента, то на множестве допустимых планов целевая функция не ограничена снизу.

С экономической точки зрения неограниченность целевой функции задачи линейного програм­мирования говорит только об одном; разработанная модель недоста­точно точна (бессмысленно говорить о бесконечной прибыли). Типичными ошибками, приводящими к построению моделей такого рода, являются:

а) неполный учет ограничений, которые являются существенными в данной задаче;

б) небрежные оценки параметров, которые участвуют в ограничениях.