
MathCadProg4
.pdf
Програмування в MathCad
Лабораторна робота № 4
Програмування циклічних обчислювальних процесів.
Програмування циклів з передумовою. Оператор циклу while .
Оператор while можна застосовувати, як для циклів з невідомою кількістю повторень, так і для циклів з відомою кількістю. Якщо кількість повторень наперед не відома, то переважно використовують оператор while , а не for .
Цикл з передумою
Шаблон оператора
ні |
умова |
так |
тіло |
циклу |
while  <логічний вираз>
<логічний вираз>
<оператори тіла циклу>
При використанні оператора while тіло циклу виконується доти, поки логічний вираз не стане рівним нулю (хибним). В іншому випадку цикл виконуватиметься безліч разів і зупинити його можна клавішею Esc.
Для внесення циклу з оператором while у робочий аркуш потрідно виконати такі дії: - натиснути кнопку while на панелі Програмування (не набирати while з клавіатури!)
-у верхньому полі ввести логічний вираз;
-у наступних полях вводимо оператори тіла циклу
-додаткові поля вводу створюємо натисканням на кнопку Add Line.
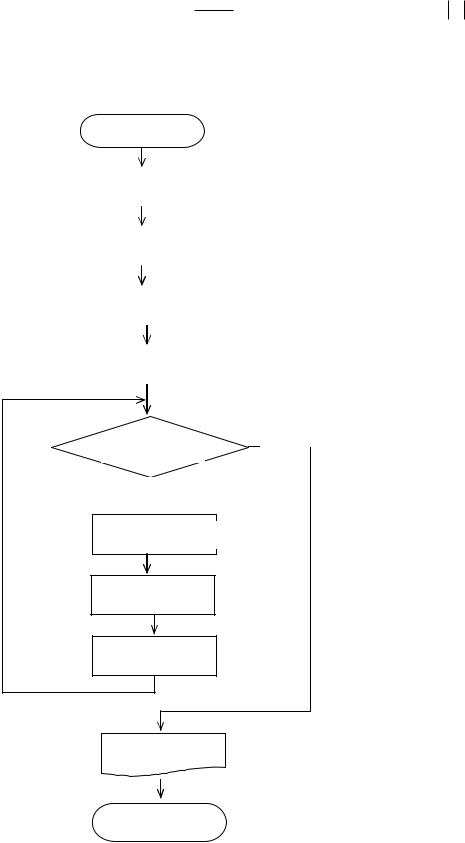
Приклад. Задана функція z =sinkxk . Визначити k, при якому z < ε .
Вхідні дані: x, ε .
|
|
|
|
|
|
K(x) := |
ε ← 0.01 |
||||||
|
|
|
K(x) |
|
|
||||||||
|
|
|
|
|
|
k ← 1 |
|||||||
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
d ← x |
||||||
|
|
|
ε=0,01 |
|
|
||||||||
|
|
|
|
|
|
|
z ← sin(x) |
||||||
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
while |
|
z |
|
≥ ε |
||
|
|
|
k = 1 |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
k ← k + 1 |
|||||
|
|
|
|
|
|
|
|
||||||
|
|
|
d = x |
|
|
|
d ← d x |
||||||
|
|
|
|
|
|
|
|
z ← |
sin(d) |
||||
|
|
|
|
|
|
|
|||||||
|
|
|
z = sin(x) |
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
return k |
||||||
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|||||||
ні
| z | ≥ ε
 так
так
k = k + 1
d = d * x
z=sin(d)/k
k
кінець

Завдання Обчислення часткової суми нескінченного ряду.
Скласти блок-схему і програмний блок для обчислення часткової суми нескінченого ряду відкинувши доданки менші по модулю за ε .


Приклад виконання завдання
Обчислити часткову суму нескінченого ряду ∑∞ (−1)n (1 + x)2n
n=1 n
відкинувши доданки менші по модулю за ε
ε= 0,001 x= - 1,34
Суму нескінченного ряду позначимо буквою s і присвоїмо їй початкове значення, яке дорівнює нулю. Кожний член ряду позначимо буквою u. Перед циклом змінній u присвоїмо значення, яке відповідає першому доданку суми.
suma := x ← −1.34 ε ← 0.001 s ← 0
n ← 1
u ← −(1 + x)2 while u > ε s ← s + u n ← n + 1
u ← (−1)n
return s
suma = - 0.109
(1 + x)2 n
n
Сумуємо значення n-го члену ряду.
Обчислюємо наступний доданок.
Цикл працює до тих пір поки черговий доданок по модулю більший за ε
