Механіка

Стоділка М.І.

Якщо в цих рівняннях зліва і справа згрупувати члени з одинаковими масами, а птім перше рівняня поділии на друге, отримаємо систему двох лінійних рівнянь, з яких легко знайти швидкості куль після удару:

Напрям швидкостей враховують знаками : ‘+’ – рух у правий бік; ‘-‘- рух у лівий.

Абсолютно непружний удар:

Після абсолютно непружного удару обидва тіла залишаються здеформрваними і рухаються як одне ціле. Нехай кулі масами m1 і m2 рухаються в одному напрямі з швидкостями u1 і u2 . Знайдемо їх спільну

швидкість u після удару. У цій ситемі тіл виконується закон збереження

імпульсу, який для центрального удару запишемо скалярним рівнянням m1ur1 + m2ur2 =(m1 + m2 )ur

звідки

ur = m1u1 + m2ur2 (3.13); m1 + m2

Внаслідок непружної деформації куль при ударі частина кінетичної енергії перетворюється у внутрішню. Цю втрату механічної енергії можна визначити по різниці кінетичних енергій до і після удару:

Тіла під час непружного удару нагріваються.

Стоділка М.І.

4. МЕХАНІКА ТВЕРДОГО ТІЛА.

§ 4.1. Момент сили відносно точки.

Нехай в точці A прикладена сила F і задана певна точка О (рис 4.1). Найкоротша віддаль l від точки О до прямої вждовж

Як видно з (рис.4.1)

l = r sinα ,

отже

[rrF ]= F l = M .

Напрям вектора [rrF ]співпадає з напрямом вектора M .

Оскільки векторний добуток дистрибутивний, тобто

[Ar(Br +C +K)]= [AB]+[AC]+K,

то момент суми сил, які мають загальну точку прикладання дорівнює сумі

моментів силr , щоr додаютьсяr r : r

M = rrF = [rr(F1 + F2 +K)]= [rrF1 ]+[rrF2 ]+K= M1 + M 2 +K.

§ 4.2. Момент пари сил.

Парою сил називають дві рівні за величиною протилежно направлені сили, які не діють вздовж однієї і тієї ж прямої.

Віддаль l між прямими, вздовж яких діють сили називається плечем пари.

Покажемо, що момент пари сил відносно довільної точки буде один і той самий.

Рис.4.2 Зробимо це спочатку для точки в площині, на якій діють сили (рис.4.2). Позначимо

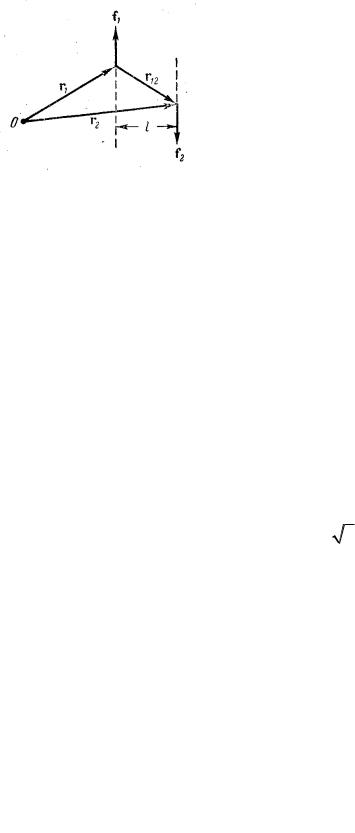
Стоділка М.І.

Розрахувати момент інерції легко тоді, коли тіло однорідне і симетричне, а момент інерції шукати відносно осі симетрії.

Знайдемо момент інерції однорідного диска відносно осі, яка перпендикулярна до площини диска і проходить через його центр (рис.4.4).

Наприклад, для диска радіуса R і товщини b :

J = ∫r 2 dm = ∫r 2 ρ dV .

Розіб'ємо диск на кільцеві шари товщиною dr . Всі точки одного шару будуть на однаковій віддалі від осі обертання, рівній r . Об'єм такого шару dV = 2π r b dr . Диск однорідний, тому ρ виносимо за знак інтегралу:

Теорема Штейнера: момент інерції відносно довільної осі дорівнює сумі моменту інерції J 0 відносно осі, яка паралельна до даної і проходить

через центр інерції тіла, і добутку маси тіла на квадрат віддалі між осями:

В таблиці 4.1 наведені формули обчислення моментів інерції для деяких однорідних тіл з масою m .

§ 4.4. Основне рівняння динаміки обертального руху.

Розіб'ємо тіло на елементарні маси та застосуємо до кожної з них другий закон Ньютона:

Fi = mi ai

і введемо замість тангенціального прискорення кутове

Стоділка М.І.

Отриманий вираз є основним законом динаміки обертального руху.

§4.5. Момент імпульсу. Закон збереження моменту імпульсу.

Зосновного закону можна зробити ряд практичних висновків.

M = Jε = J ddtω ; Mdt = Jdω = d( Jω )

Для вияснення фізичного змісту Jω розглянемо рух матеріальних точок тіла, яке обертається. Кожна з цих точок масою mi рухається по

колу радіусом ri , її швидкість ui . Вектор швидкості і вектор імпульсу miui перпендикулярні до ri . Отже, ri є плечем по відношенню до miuri ; можна

(аналогічно з моментом сили) ввести поняття моменту імпульсу точки:

Li = miuiri .

Алгебраїчна сума моментів імпульсу всіх точок тіла, яке обертається носить назву моменту імпульсу відносно осі:

L = ∑Li .

Стоділка М.І.

§ 4.6. Кінетична енергія тіла, яке обертається навколо нерухомої осі.

Кінетична енергія i -ї матеріальної точки:

Для тіла, яке обертається і рухається поступально:

§ 4.7. Робота і потужність зовнішніх сил при обертанні твердого тіла.

За час dt i -та елементарна маса проходить шлях dsi : dsi = ri dϕ , де dϕ - кут, на який повернеться тіло за час dt .

Робота сили Fi визначається проекцією сили на напрям переміщення,

яке, очевидно, дорівнює тангенціальній складовій: dAi = Fτ idSi = Fτ iridϕ .

Але Fτ iri дорівнює модулеві моменту сили:

M i = Fτ i ri ,

а

dϕ =ω dt .

Отже:

dAi = M i dϕ .

Робота всіх сил дорівнює сумі:

Це робота за час dt .

За скінчений проміжок часу

ϕt

A = ∫dA = ∫Mdϕ = ∫Mω dt .

Якщо M = const :

t

A = M ∫ω dt ,

0

A = Mϕ .

Згідно з законом збереження робота повинна дорівнювати збільшенню кінетичної енергії dT . Переконаємося в цьому:

Потужність чисельно дорівнює роботі, яка виконується за одиницю часу:

N = dAdt = M ddtϕ = Mω.

Зіставимо закономірності і основні величини поступального і обертального рухів:

Стоділка М.І.

5. Механіка рідин

§ 5.1. Статика

Рідина, як і газ приймає форму посудини. Але в рідинах на відміну від газів віддалі між молекулами залишаються майже незмінними, тому рідина має практично завжди постійний об’єм.

Зовнішню дію на межу рідини чи газу зручніше характеризувати не вектором сили, як це робиться в механіці, а створеним цією силою тиском.

Тиском називають величину, яка дорівнює відношенню сили, що діє нормально на елемент поверхні, до її площі, тобто

p = ∆∆FS

За цим виразом визначають середнє значення тиску. Якщо сила, з якою рідина діє на поверхню площею ∆S розподілена нерівномірно, то вводять поняття тиску в даній точці рідини (або газу). Його величина визначається формулою:

Тиск величина скалярна і для заданої точки рідини або газу не залежить від орієнтації площини . З означення випливає одиниця тиску в

СІ: Н м2 , яку називають “паскаль” (Па). Тиск 1 Падуже малий, тому на практиці використовують кПа, МПА і позасистемні одиниці.

Позасистемні одиниці тиску:

1 атм = 1,0332 ат = 760 мм.рт.ст = 10 332 мм.вод.ст

Закон Паскаля (1623 – 1662)

Тиск в довільному місці нерухомої рідини однаковий по всіх напрямках, причому тиск однаково передається по всьому об’єму.

При поперечному перерізі S стовпа рідини і його висоті h та густині ρ вага

P = ρgSh ,

а тиск на нижню основу

p = ρgShS = ρgh ,

тобто тиск змінюється лінійно з висотою.

Стоділка М.І.

Тиск ρgh називається гідростатичний.

Згідно з цією формулою тиск на нижні шари буде більшим ніж на поверхні, тому на тіло, занурене в рідину діє виштовхувальна сила, яка дорівнює вазі витісненої тілом рідини: FA = ρgV , де: ρ - густина рідини;

V – об’єм зануреної частини тіла.

§ 5.2. Гідродинаміка

Гідродинамікаце розділ механіки, у якому вивчаєтьсч рух нестисливих рідин і взаємодія їх з твердими тілами.

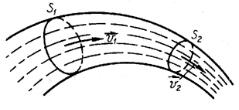
Потік, в якому поле швидкостей з часом залишається незмінним називається стаціонарним.

Графічно потік зображають не векторами, а лініями потоку. Вони проводяться так, щоб у кожній точці вектор швидкості був дотичною до лінії потоку. Цих ліній проводять стільки, щоб густина їх була пропорційна величині швидкості в усіх місцях потоку.

Зауважимо, що лінії потоку не треба ототожнювати з траєкторіями частинок; лише для стаціонарного потоку лінії потоку збігаються з трвєкторіями частинок.

Частину рідини або газу, обмежену лініями потоку, називають трубкою потоку.

S u ρ будуть шукані кількості рідин. У стаціонарному потоці ці кількості

рідини або газу повинні бути однакові:

ρ1u1S1 = ρ2u2S2 ,

бо інакше між розглядуваними перерізами кількість рідини весь час змінювалася б і не існувало б стаціонарного потоку.

Розрахунки показують, що в стаціонарному потоці змінами густини не тільки рідини, але і газу можна знехтувати. Тому:

S1u1 = S2u2 ,

Це теорема про нерозривність потоку.

З теореми про нерозривність потоку видно, що швидкість потоку менша там де трубка ширша і навпаки. Отже при переході з ширшого перерізу у вужчий рідина або газ переміщуються з додатнім прискоренням. Постає питання – під дією якої сили? Відповідь на це питання дає рівняння Бернуллі.

Стоділка М.І.

§ 5.3. Рівняння Бернуллі

Звичайно рідини і гази в потоках перебувають під тиском, який створюється насосними станціями, власною силою тяжіння. Тиск міняється при переході з ширшого перерізу у вужчий. Але ці зміни істотно не впливають на об’єм і густину речовини в стаціонарному потоці. Коефіцієнт стисливості рідин дуже малий, наприклад, для води при 15ºС і тисках до 100 ат. він дорівнює 0,00005 1/ат. Для газів швидкості яких менші від швидкості звуку, змінами густини в потоці теж можна знехтувати. Можна знехтувати і в’язкістю, тобто розглядати ідеальну рідину – абсолютно нестисливу і нев’язку.

Для стаціонарного потоку ідеальних рідин і для газів справджується рівняння Бернуллі.

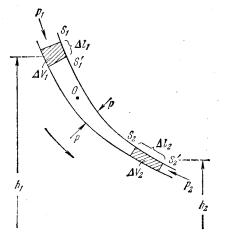
Виділимо з потоку вузьку трубку рідини, обмежену перерізами S1 і S2 . За час t розглядувана рідина зміститься в трубці і верхня межа S1 переміститься в S1' , а нижня межа S2

займе положення S2' (рис.5.2).

Зміна енергії рідини повинна дорівнювати роботі, виконаній силами тиску над рідиною. Знайдемо ці величини.

Енергія рідини дорівнює сумі кінетичної і потенціальної енергій окремих її частинок. З рис.5.2 видно, що енергія рідини змінилась за рахунок тих

Рис.5.2 частинок поблизу верхньої і нижньої меж (у заштрихованих об’ємах), які за

час t залишили місця.

Енергія частинок, які залишилися в не заштрихованій області (через час t ) така сама, як і тих, що займали цю частину об’єму на початку.

Із сказаного випливає, що зміна енергії дорівнюватиме різниці енергій частинок у заштрихованих областях ∆V1 і ∆V2 . Оскільки потік

неперервний і рідина нестислива, то ∆V1 = ∆V2 = ∆V .

Нехай ці об’єми настільки малі, що для частинок у кожному з них можна вважати однаковою швидкість v, висоту h і тиск p. Тоді для різниці енергій матимемо:

нижньої меж рідини.