
- •2.1. Выполнить расчет потенциала и напряженности поля в конденсаторе.
- •Часть 1. Расчёт электрического поля в пространстве между электродами сферического конденсатора без объёмного заряда. 7
- •Часть 2. Расчёт электрического поля в пространстве между электродами сферического конденсатора с объёмным зарядом. 16
- •Теоретическое обоснование
- •Часть 1. Расчёт электрического поля в пространстве между электродами сферического конденсатора без объёмного заряда.
- •1.1. Расчёт потенциала и напряжённости поля в конденсаторе.
- •1.2. Определение радиуса границы раздела r12, при котором напряжение делится поровну между слоями.
- •1.3. Определение поверхностной плотности зарядов электродов и ёмкости
- •Часть 2. Расчёт электрического поля в пространстве между электродами сферического конденсатора с объёмным зарядом.
- •2.1. Расчёт потенциала и напряжённости поля в конденсаторе.
- •Список используемой литературы
1.3. Определение поверхностной плотности зарядов электродов и ёмкости
Для определения
поверхностной плотности заряда
воспользуемся одним из граничных
условий:
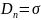 ,
где
,
где
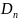 –
нормальная к поверхности электрода
часть электрического смещения.
–
нормальная к поверхности электрода
часть электрического смещения.
Учитывая симметрию
поля относительно оси конденсатора
получаем, что на внутреннем электроде
поверхностная плотность заряда
определяется выражением: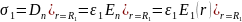 (1)
(1)
Подставляя числа, получим:

Аналогично получим
поверхностную плотность заряда на
внешнем электроде, с учётом знака
,
так как вектор
направлен к внешнему электроду:
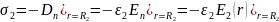 (2)
(2)
Подставляя значения, получим:
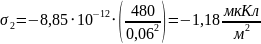
Найдем заряды электродов и суммарный заряд конденсатора
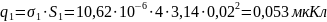 (3)
(3)
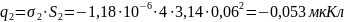 (4)
(4)
Суммарный заряд конденсатора равен сумме зарядов на обкладках конденсатора:
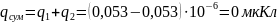
Ёмкость определяется следующим образом:
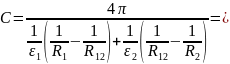
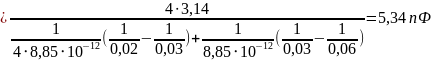

Часть 2. Расчёт электрического поля в пространстве между электродами сферического конденсатора с объёмным зарядом.
2.1. Расчёт потенциала и напряжённости поля в конденсаторе.
Дано:
|
|
|
|
|
, кВ |
ρ, 10—4 Кл/м3 |
0,02 |
0,06 |
0,03 |
|
|
10 |
20 |
Решение:
Область расчёта электрического поля конденсатора представляет собой пространство между его электродами и состоит из двух подобластей: 1 – внутренний слой диэлектрика и 2 – внешний слой. Согласно условию задачи, во внутреннем слое диэлектрика присутствует объёмный заряд, и распределение потенциала находится с помощью уравнения Пуассона. Принимая во внимание условие, что поле конденсатора изменяется вдоль координаты, перпендикулярной поверхности электродов (координаты r) выбираем сферическую систему координат для записи уравнения:
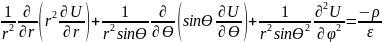
Учитывая симметрию
поля относительно оси конденсатора,
принимаем Eφ=0
и, следовательно,
 Кроме того, поле сферического конденсатора
является плоскопараллельным (картина
поля во всех плоскостях, перпендикулярных
оси конденсатора, одинакова), и,
следовательно, Ez=0
и
Кроме того, поле сферического конденсатора
является плоскопараллельным (картина
поля во всех плоскостях, перпендикулярных
оси конденсатора, одинакова), и,
следовательно, Ez=0
и
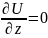 .
Таким образом, уравнение Пуассона
принимает вид:
.
Таким образом, уравнение Пуассона
принимает вид:

Для внешнего слоя распределение потенциала находится с помощью уравнения Лапласа, так как там нет объёмного заряда. И оно принимает вид:
Рассмотрим зависимость потенциала от радиуса сферы.
Вследствие наличия между обкладками двухслойного диэлектрика необходимо рассмотреть два случая. Однако, так как во внутреннем слое присутствует объёмный заряд, то зависимости будут различными.
При ≤ r ≤ :
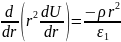
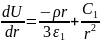

При ≤ r ≤ после двукратного интегрирования уравнения Лапласа по переменной r получаем функцию:
При этом, используя формулу
находим распределение напряжённости электрического поля:
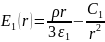
Для определения постоянных интегрирования воспользуемся граничными условиями:
1.
При r=
потенциал
равен U=
,
тогда:
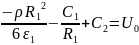
2.
При r=
потенциал равен U=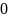 ,
тогда:
,
тогда:
3. При r= на границе раздела двух диэлектриков нормальные составляющие вектора электрического смещения равны, тогда: D1n=D2n→
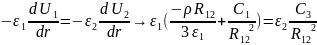
4.
При r=
на границе раздела двух диэлектриков
потенциалы
и
равны, тогда:
;
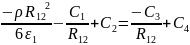
Запишем систему уравнений для нахождения постоянных:
 (1)
(1)
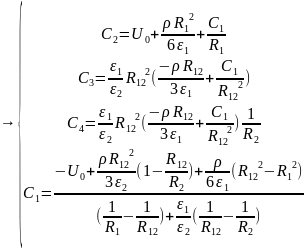
Подставим численные значения:
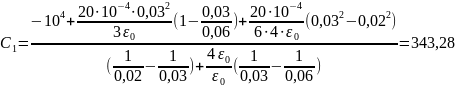 В
В
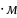 ;
;
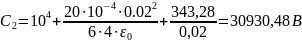 ;
;
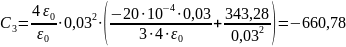 В
;
В
;
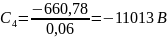
Таким образом, выражения распределения потенциала и напряжённости электростатического поля между электродами сферического конденсатора будет иметь вид:
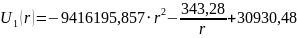
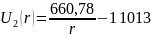

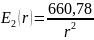
Для определения поверхностной плотности заряда на электродах, воспользуемся формулами (1) и (2), которые представлены в пп1.3:
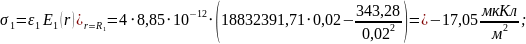
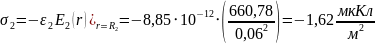
Для определения заряда на электродах, воспользуемся формулами (3) и (4), которые представлены в пп1.3:
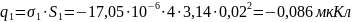
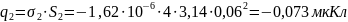
Для нахождения объемного заряда, распределенного во внутреннем слое диэлектрика, найдем объем данной области:
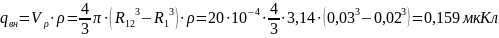
Суммарный заряд конденсатора равен сумме зарядов на обкладках конденсатора и заряда, распределенного во внутреннем слое диэлектрика:

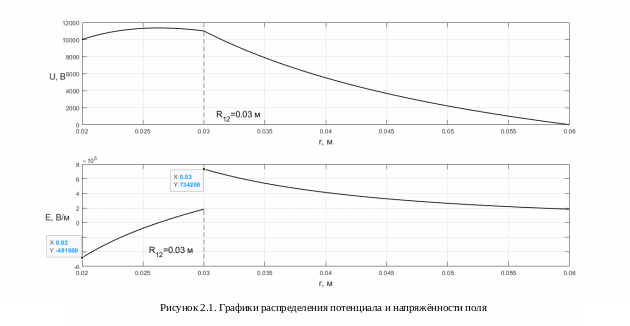 Максимальное
по модулю значение напряженности поля
конденсатора достигается при
:
|Emax|=734200 В/м.
Максимальное
по модулю значение напряженности поля
конденсатора достигается при
:
|Emax|=734200 В/м.
2.2. Расчёт потенциала и напряжённости при изменённом значении радиуса границы раздела R12 (R12 = 1,2R1 и R12 = 0,8 R2).
Используем
выражениями для постоянных интегрирования
из п. 2.1
и подставим
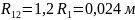 :
:
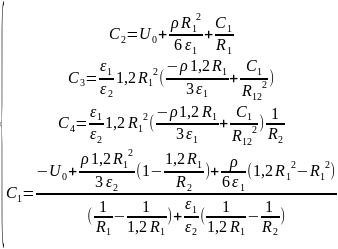
Подставим численные значения:
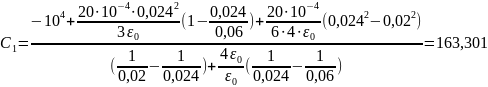 В
;
В
;
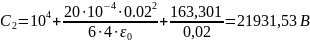 ;
;
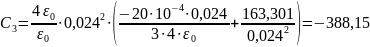 В
;
В
;
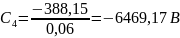
Таким образом, выражения распределения потенциала и напряжённости электростатического поля между электродами сферического конденсатора будет иметь вид:
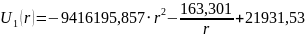
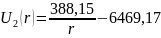
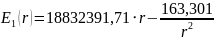
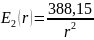
Для определения поверхностной плотности заряда на электродах, воспользуемся формулами (1) и (2):
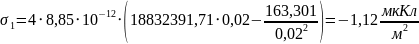

Для определения заряда на электродах, воспользуемся формулами (3) и (4), которые представлены в пп1.3:
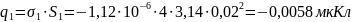
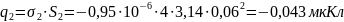
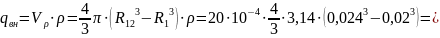
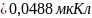
Суммарный заряд конденсатора:
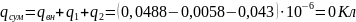
Аналогично
при
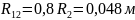 :
:
Подставим численные значения:
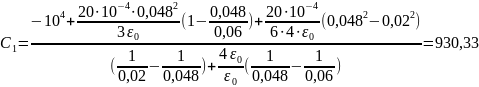 В
;
В
;
 ;
;
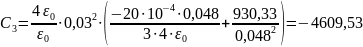 В
;
В
;
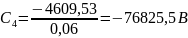
Таким образом, выражения распределения потенциала и напряжённости электростатического поля между электродами сферического конденсатора будет иметь вид:

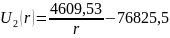


Для определения поверхностной плотности заряда на электродах, воспользуемся формулами (1) и (2):
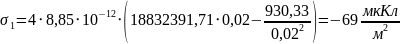
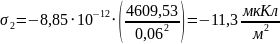
Для определения заряда на электродах, воспользуемся формулами (3) и (4), которые представлены в пп1.3:

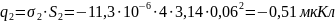
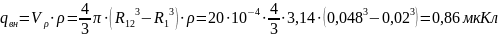
Суммарный заряд конденсатора:
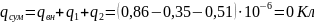
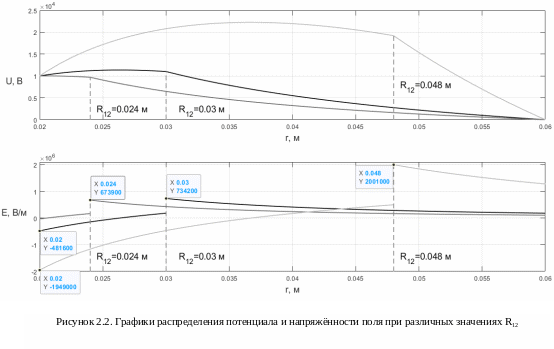
При максимальное по модулю значение напряженности поля конденсатора достигается при : |Emax|=673900В/м.
При
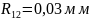 аксимальное
по модулю значение напряженности поля
конденсатора достигается при
:
|Emax|=734200 В/м.
аксимальное
по модулю значение напряженности поля
конденсатора достигается при
:
|Emax|=734200 В/м.
При максимальное по модулю значение напряженности поля конденсатора достигается при : |Emax|=2001000 В/м.
2.3. Расчёт потенциала и напряжённости при изменённом значении диэлектрической проницаемости внутреннего слоя изоляции ε1 (ε1 = ε0 и ε1 = 6ε0).
Используем
выражениями для постоянных интегрирования
из п. 2.1
и подставим
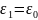 :
:
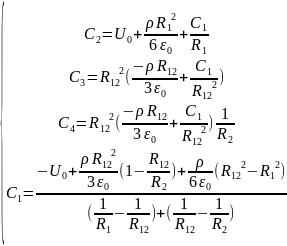
Подставим численные значения:
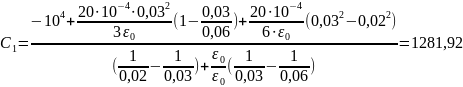 В
;
В
;
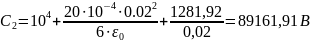 ;
;
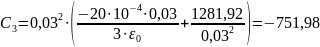 В
;
В
;
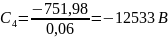
Таким образом, выражения распределения потенциала и напряжённости электростатического поля между электродами сферического конденсатора будет иметь вид:
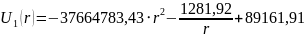
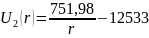
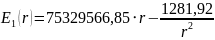
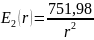
Для определения поверхностной плотности заряда на электродах, воспользуемся формулами (1) и (2):
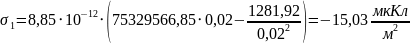
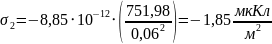
Для определения заряда на электродах, воспользуемся формулами (3) и (4), которые представлены в пп1.3:
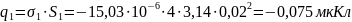
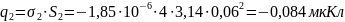
Суммарный заряд конденсатора:
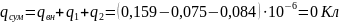
Аналогично
при
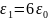 :
:
Подставим численные значения:
 В
;
В
;
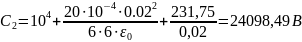 ;
;
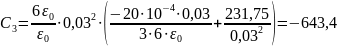 В
;
В
;
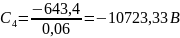
Таким образом, выражения распределения потенциала и напряжённости электростатического поля между электродами сферического конденсатора будет иметь вид:
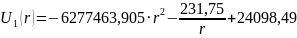
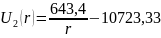

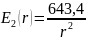
Для определения поверхностной плотности заряда на электродах, воспользуемся формулами (1) и (2):
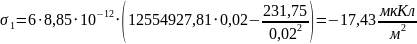
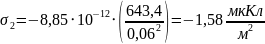
Для определения заряда на электродах, воспользуемся формулами (3) и (4), которые представлены в пп1.3:
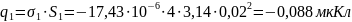
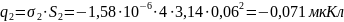
Суммарный заряд конденсатора:
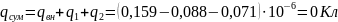
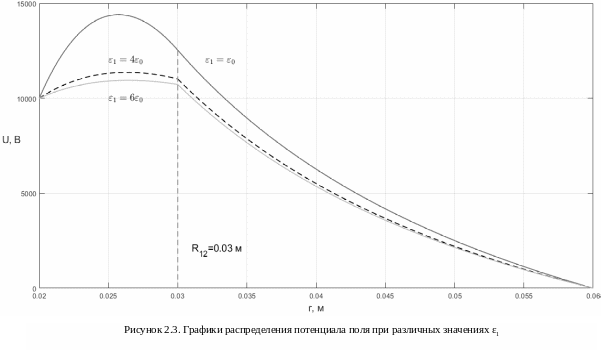
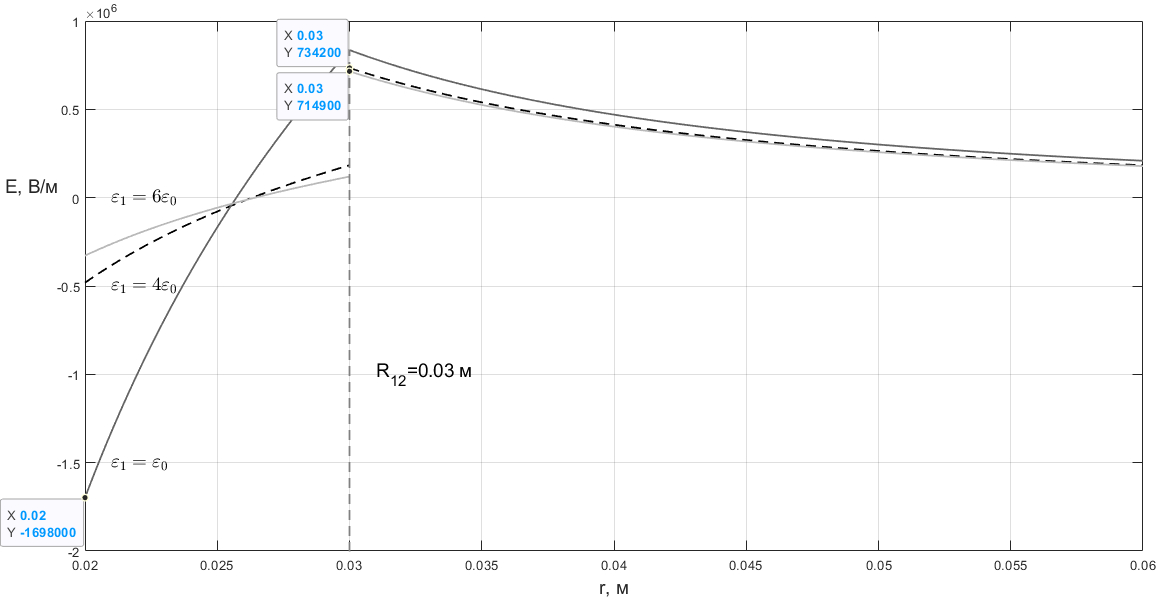
Рисунок 2.4. Графики распределения напряженности поля при различных значениях ε1
При максимальное по модулю значение напряженности поля конденсатора достигается при : |Emax|=1698000 В/м.
При
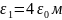 аксимальное
по модулю значение напряженности поля
конденсатора достигается при
:
|Emax|=734200 В/м.
аксимальное
по модулю значение напряженности поля
конденсатора достигается при
:
|Emax|=734200 В/м.
При максимальное по модулю значение напряженности поля конденсатора достигается при : |Emax|=714900 В/м.
Выводы
В сферическом
конденсаторе с двухслойной изоляцией
с различной диэлектрической проницаемостью
слоёв и без объёмного заряда, потенциал
и напряженность убывают (рисунок 1.1).
Были рассчитаны поверхностные плотности
заряда на электродах, заряды электродов,
суммарный заряд конденсатора и определена
его ёмкость (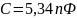 ).
).
При внесении объёмного заряда во внутренний слой изоляции, форма кривых потенциала и напряжённости изменилась (рисунок 2.1). На участке
≤ r ≤ потенциал возрастает, а на ≤ r ≤ убывает. Модуль напряженности на первом участке сначала убывает, затем возрастает. А после скачка напряженность убывает. Также рассчитанные поверхностные плотности заряда на электродах одного знака, заряды электродов одного знака, суммарный заряд конденсатора с учетом объёмного заряда равен нулю. Максимальный модуль напряжённости электрического поля увеличился.
Были построены графики распределения потенциала и напряжённости при различных значениях радиуса границы раздела R12 (рисунок 2.2). Чем больше R12, тем при большем r напряжённость поля меняет своё направление. Также, чем меньше R12, тем меньше максимальный модуль напряжённости. Кривые имеют большую крутизну при большем R12.
Были построены графики распределения потенциала и напряжённости при различных значениях диэлектрической проницаемости внутреннего слоя изоляции ε1 (рисунок 2.3, рисунок 2.4). При ε1 = ε0 нет разрыва на графике напряжённости. Чем меньше значение ε1, тем больше крутизна U(r) и E(r). При меньшем значении ε1 максимальный модуль напряжённости больше.
