ИЭ / 4 семестр / Лекции / Лекц 04

7

Лекция 4

Метод зеркальных изображений.

Метод применим для расчета полей, созданных системой источников поля (зарядов в электростатическом поле либо токов в магнитном поле и в электрическом поле постоянных токов), расположенных вблизи плоской бесконечно протяженной границы, разделяющей области с различными характеристиками среды (, , ). Рассмотрим метод на примере электростатического поля, созданного системой зарядов вблизи плоской проводящей границы.

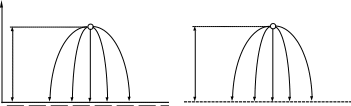
Пусть в диэлектрике на высоте h над проводящей плоскостью находится заряженное тело с зарядом +q (рис.4–1а).

jy

+q jy +q

h h

 x  x

  U = const  U = const

а) h

–q

б)

Рисунок 4–1

Поле, созданное зарядом q , приведет к уходу с поверхности проводника одноименных зарядов, т.е. к появлению на поверхности слоя зарядов противоположного знака, распределенных по поверхности с некоторой плотностью (), величина которой в разных точках различна. Линии напряженности начинаются на теле с положительным зарядом (+q) и заканчиваются на проводящей плоскости с зарядом (– ), причем линии напряженности будут подходить к проводящей равнопотенциальной поверхности под прямым углом. Рассчитать такое поле можно, лишь зная закон распределения поверхностного заряда  на проводящей плоскости:  = D = E = . Для этого необходимо знать зависимость потенциала от координат U (x, y, z) , что невозможно не зная закон распределения заряда  (x, y, z).

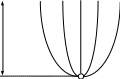
Рассмотрим поле в диэлектрике, созданное двумя заряженными одинаковыми телами с равными и противоположными по знаку зарядами (+q, – q ), расположенными на расстоянии 2h друг от друга (рис. 4–1б). Созданная такой системой зарядов картина поля симметрична относительно плоскости, все точки которой равноудалены от заряженных тел. Линии напряженности электрического поля в силу симметрии перпендикулярны этой плоскости. Поэтому плоскость симметрии является поверхностью равного потенциала.

Сопоставляя полученную (рис.4–1б) и исходную (рис.4–1а) картины полей, можем утверждать, что из-за одинаковой геометрии и граничных условий картины поля в верхней полуплоскости идентичны, а, следовательно, все характеристики поля полностью совпадают.

Таким образом, метод зеркальных изображений позволяет заменить проводящую среду, ограниченную плоской поверхностью, диэлектриком с зеркальным изображением заряженного тела и с изменением знака заряда на противоположный. При этом поле в исходной области остается неизменным.

Расчет поля системы двух зарядов в диэлектрике существенно проще, чем в исходной задаче, т.е. метод зеркальных изображений позволяет упростить расчет поля. Этот метод применим для любого количества заряженных тел, а в плоскопараллельных полях для любого числа параллельных земле проводов с зарядами.

Рассчитав потенциал этим методом, легко определить через его производную на плоскости симметрии распределение зарядов на поверхности проводника.

| _y=0

Применение метода зеркальных изображений возможно и в случае, когда заряды находятся внутри диэлектрика между гранями двугранного угла «», образованного проводящими поверхностями, если , где «n» целое число. Для угла (рис.4–2) имеем:

-₂ +₁

+₂¹ -₁¹

Рисунок 4-2

Отразим заряд +₁ от вертикальной стенки, вследствие чего появится второй заряд противоположного знака –₂ , и оба эти заряда оказались расположенными над горизонтальной проводящей плоскостью. Отразим эти заряды в горизонтальной плоскости и получим еще два заряда ( ₂¹ и –₁¹). Полная система из четырех зарядов образует картину поля в диэлектрике, часть которой в первом квадранте совпадает с исходной картиной поля.

Метод зеркальных изображение применяется и при отражении зарядов в цилиндрических и в сферических проводящих поверхностях. Он также применим при отражении в поверхностях раздела диэлектриков с различными диэлектрическими проницаемостями для плоской, цилиндрической и сферической границы. Более подробно эти вопросы рассматриваются в курсе «Расчет электромагнитных полей».

Метод конформных отображений.

Расчет поля методом конформных отображений основан на том, что существует возможность отобразить с помощью некоторого математического преобразования заданную область в комплексной плоскости « z » (x + jy) на так называемую каноническую область в комплексной плоскости « ω » ( ξ+j).

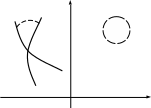
В качестве канонической области обычно используется верхняя полуплоскость, а также круг либо полоса. Преобразование называется конформным, так как при переходе от одной области к другой либо обратно сохраняются углы в точках пересечения между любыми линиями в обеих областях _z = _ω (рис.4-3).

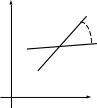
jy j

z _ω

1 _z 1 2

ω

2

z_k ω_k

x ξ

Рисунок 4–3

Для изучения полей это очень важно, так как мы знаем, что линии равного потенциала и линии напряженности всегда пересекаются под прямым углом.

Существует общий подход к преобразованию произвольной многоугольной области, ограниченной ломаной линией на верхнюю полуплоскость и обратно с помощью интеграла Кристоффеля-Шварца.

Для многих часто встречающихся конфигураций областей получены соотношения, необходимые для преобразования, они приведены в справочной литературе. Рассмотрим некоторые простые примеры.

1. Двугранный угол () – поле между двумя проводящими плоскостями, сходящимися под углом (рис. 4–4а).

j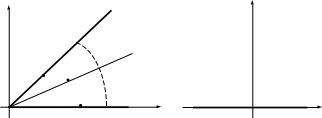 y j

z

U = 0 ω

 C

B C

A U = 0 x B A ξ

0 а) 0 б)

Рисунок 4–4

П роводящие грани имеют одинаковый потенциал (U = 0), совместим ось (x) со следом одной из граней. Преобразование такой области на верхнюю полуплоскость (ω) осуществляется по формуле:

Положение любой точки на первой грани (точка А), координаты которой в исходной системе координат записываются в виде: , в области ω определяется координатой и располагаются на положительной части вещественной оси ξ. (рис. 4–3б). Изменяется лишь линейный масштаб. Положение любой точки на второй грани (точка B), координаты которой в исходной системе координат записываются в виде: , в области ω определяется координатой и располагаются на отрицательной части вещественной оси ξ. 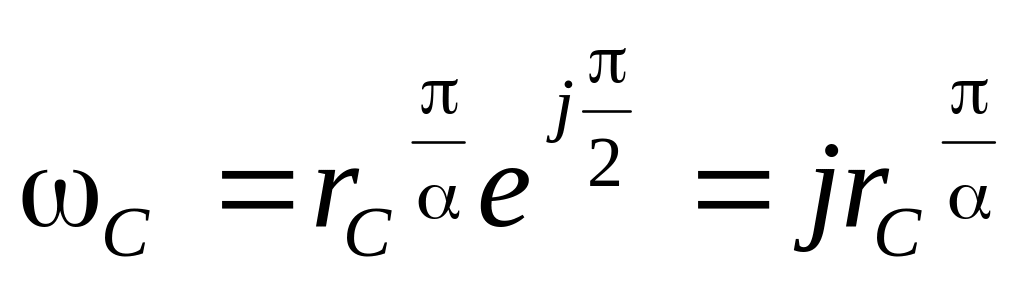Положение любой точки на биссектрисе угла (точка С), координаты которой в исходной системе координат записываются в виде: , в области ω определяется координатой и располагаются на мнимой оси j (см. рис.4–4б).

2. Бесконечно глубокий проводящий паз, шириной (d) (рисунок 4–5а).

jy j

A F D z ω

E

E F

d

x ξ

B 0 C A B 0 C D

а) б)

Рисунок 4–5

П ометим начало координат посредине дна паза и направим ось (x) вдоль дна вправо. Преобразование такой области на верхнюю полуплоскость (ω) осуществляется по формуле:

.

Положение угловых точек (В и С), координаты которых в исходной системе координат записывается в виде: , в области ω также расположены на вещественной оси ξ и определяется координатами:

.

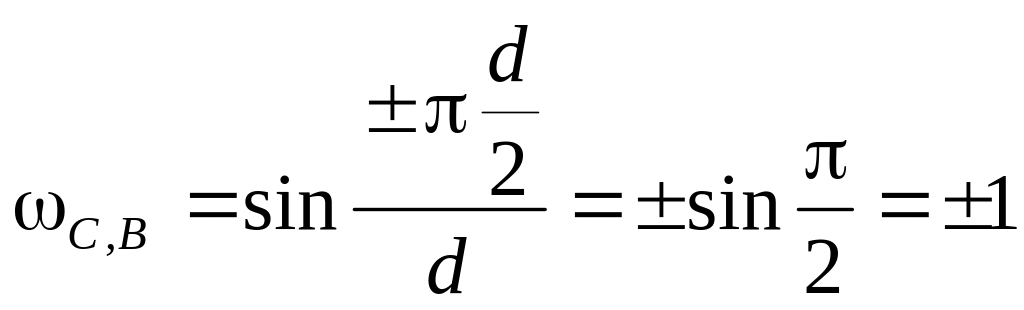Положение точек (A и D), координаты которых в исходной системе координат записывается в виде: , в области ω расположены на вещественной оси ξ и определяется координатами:

.

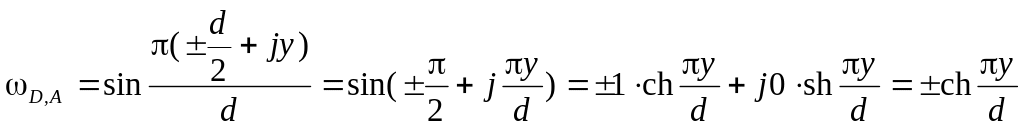Положение точки (E), координата которой в исходной системе записывается в виде: , в области ω расположена на мнимой оси j и определяется координатой:

. (см. рис.4–5б).

3. Плоскость с вертикальным выступом (стеной), высотой (h) (рисунок 4–6а).

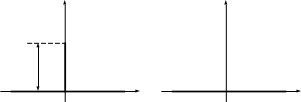jy j

B z ω

C B ω₀

z₀

h

x ξ

A 0 D A 0 C 0 D

а) б)

Рисунок 4–6

Н ачало координат поместим у основания выступа и направим ось (x) вдоль горизонтальной плоскости. Преобразование такой области на верхнюю полуплоскость (ω) осуществляется по формуле:

.

Положение точки (С), координата которой в исходной системе записывается в виде: , в области ω расположена в начале координат, так как определяется координатой:

. Положение точки (0), координата которой в исходной системе записывается в виде: , в области ω вследствие двузначности корня дает два значения на вещественной оси ξ и определяется координатами: . Положение точек (A и D), координаты которых в исходной системе записывается в виде: , в области ω расположены на вещественной оси ξ и определяется координатами: Положение точки (B), координата которой в исходной системе записывается в виде: (y>h), в области ω расположена на мнимой оси j и определяется координатой: (см. рис.4–6б).

Получение выражения для комплексного потенциала в исходной области на плоскости (z) и определение зависимости плотности заряда () на поверхности проводников рассмотрим на примере плоскости с выступом.

Пусть в исходной системе заряженный провод с зарядом (+) находится в точке с координатой (z₀ = x₀ + jy₀). После преобразования исходной области на каноническую область на основе используемой формулы преобразования найдем место расположения заряженного провода в области ω (рис.4-6): . Затем, используя метод зеркальных изображений, заменим проводящую среду диэлектриком с проницаемостью  и с зеркально расположенным зарядом (–) . Его координата является сопряженной с координатой исходного заряда: .

Запишем известное выражение для комплексного потенциала в системе двух заряженных осей (проводов).

,

здесь ω – координата произвольной точки поля. В области ω линии равного потенциала и линии напряженности являются, как мы уже знаем, окружностями. Для перехода к исходной области выразим ω через z, тогда получим:

.

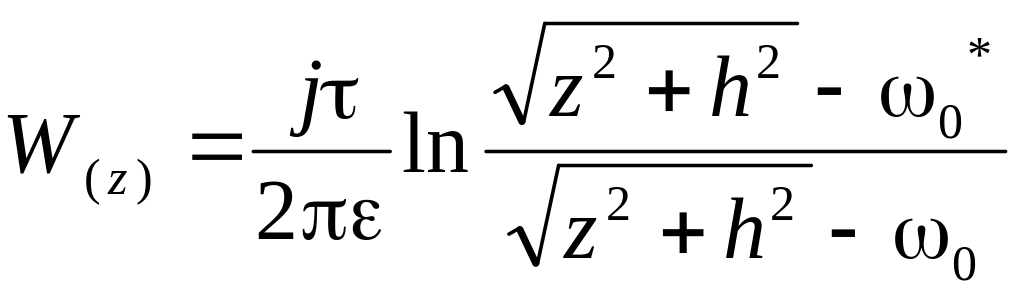Величину напряженности в любой точке определяем через производную от комплексного потенциала:

.

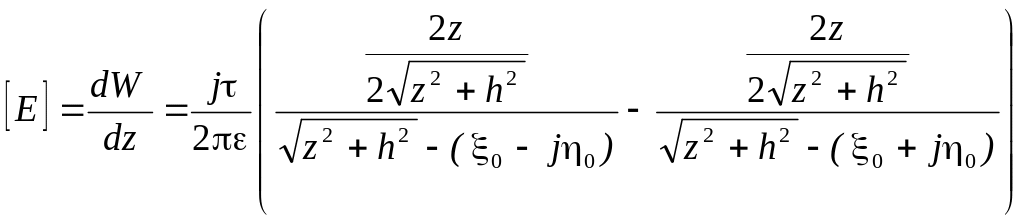После упрощения получим:

.

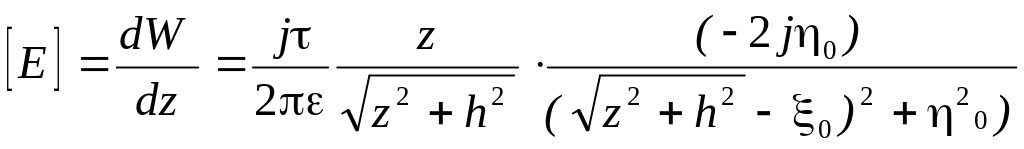Подставляя координаты поверхности проводников и умножая на , получим значения поверхностной плотности заряда на поверхности проводников:  = D =  E .

Графический метод построения картины плоскопараллельного поля.

Очень часто границы проводящих поверхностей не могут быть описаны математическими выражениями, поэтому аналитический расчет полей в этих условиях оказывается невозможным. В этом случае необходимо воспользоваться графическим методом построения картины поля. При графическом построении необходимо соблюдать одновременно три условия.

1. Ортогональность линий равного потенциала и линий напряженности во всех точках их пересечения

2. Линии напряженности должны подходить перпендикулярно к поверхности проводящих тел.

3. Ячейки ортогональной сетки, образованной линиями U = const и V = const должны быть подобны друг другу.

Два первых условия нам уже известны. Третье условие вызвано необходимостью построения картины поля с постоянным приращением потенциала между любыми соседними линиями равного потенциала (U = const) и постоянным приращением функции потока между любыми соседними линиями напряженности (V = const). Запишем величину модуля напряженности через приращения в криволинейной ортогональной системе координат, связанной с линиями поля:

, откуда: = k = const.

Это означает, что все ячейки при построении картины поля должны быть подобными (рис. 4–7). Удобнее выбирать  V = U, тогда  a = n , при этом все ячейки должны быть криволинейными квадратами (k = 1).

U₁ V₁

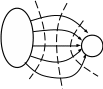
U₂ a

V₂

+ n

–

Рисунок 4–7