Лекция 3
Учебник К.С.Демирчян, Л.Р.Нейман, Н.В.Коровкин, В.Л.Чечурин «Теоретические основы электротехники» , том 3, изд.4, 2003 (или любое другое издание этого учебника).
Понятия о плоскопараллельном поле, функции потока, комплексном потенциале поля изложены в параграфах 24.8, 24.9 (стр.44-49).
Поле двухпроводной линии передачи, поле несоосных цилиндров изложены в параграфах 24.12, 24.13 (стр.52-56).
Остальной материал лекции изложен ниже.
Применение функций комплексного переменного.
Если плоскость x,y рассматривать как плоскость комплексного переменного z = x+jy = r·e j, то функции U(x,y) и V(x,y) можно рассматривать как составляющие некоторой комплексной функции W = W(z) = W(x,y), называемой комплексным потенциалом плоскопараллельного электрического поля:
W = V + j U.
Здесь V и U – вещественная и мнимая части комплексного потенциала, а z – комплексная координата точки на плоскости x,y , а не третья координатная ось декартовой системы.
Учитывая, что составляющие вектора напряженности определяются через производные от потенциала и функции потока, модуль вектора напряженности можно определить через производную от комплексного потенциала:
Математический аппарат теории функции комплексного переменного развит достаточно глубоко, и его удобно использовать для расчета плоскопараллельных полей. Рассмотрим некоторые способы применения комплексного потенциала для анализа полей.
Метод заданного комплексного потенциала.
Этот метод расчета плоскопараллельных полей заключается в предварительном задании некоторой комплексной функции на плоскости – комплексного потенциала W(z) и последующего определения, какой геометрической области предложенная функция W(z) соответствует. Координаты точки на плоскости могут быть заданы в декартовой или полярной системе: z = x+jy = r·e j. Рассмотрим некоторые простые примеры.
. Пусть комплексный потенциал задан в виде:W(z) = az + b = (ax + b) + jay =
= V + jU , тогда:
V = ax + b = const уравнение линии напряженности, т.е. x = const вертикальные линии, а
U = ay = const уравнение линии равного потенциала т.е. y = const горизонтальные линии.
При а > 0 с ростом x и y растут соответственно V и U . Принимая постоянным приращения потенциала и функции потока (V = const и U = const), получаем постоянство приращения координат при переходе от линии к линии ( x = const и y = const ) (рис.3–4).
Совместив поверхности двух проводников с двумя линиями равного потенциала (U1 и U4), получаем картину поля между двумя плоскими проводящими пластинами (внутри плоского конденсатора). Таким образом, мы установили, какой геометрической области соответствует принятый комплексный потенциал.
. Пусть комплексный потенциал задан в виде:
W(z) = jA ln z = jA ln(r·ej) = jA ( ln r + j) = – A + jA ln r = V + jU, тогда:
V = – A = const уравнение линии напряженности, т.е. = const. Эти линии представляют собой лучи, исходящие из начала координат;
U = A ln r = const уравнение линии равного потенциала, т.е. r = const Эти линии представляют собой концентрические окружности с центром в начале координат.
Принимая
постоянным приращения потенциала и
функции потока (V
= const и U
= const), получаем постоянство
приращения координаты
= const при переходе от
одной к другой линии напряженности и
постоянство отношений радиусов соседних
линий равного потенциала
.
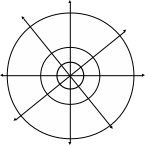
Совместив поверхность проводника с одной из линий равного потенциала, получим картину поля уединенного заряженного кругового цилиндра (рис. 3–5)
V3
V4 V2
U3 U2
V1
U1
Рисунок 3–5
При =2 получаем поверхность, охватывающую весь проводник с полным зарядом, тогда
; 
; 
; 
.
Окончательно выражения для функции потока и потенциала имеют вид:
; 
.
При положительном заряде на цилиндре ( >0) потенциал убывает с ростом радиуса (U1> U2> U3) , вектор напряженности направлен в сторону убывания потенциала, а функция потока возрастает с ростом угла , т. е. против часовой стрелки (V1< V2 < V3 …). Аналогичная картина поля создается тонкой заряженной нитью, расположенной в начале координат
Если заряженную нить (рис. 3–6) поместить не в начало координат (z = 0), а в точке с координатой (z = z0), то выражение для комплексного потенциала имеет вид:
W = j A ln( z – z0)
j y
z
z – z0
x
0
z0
Рисунок 3–6
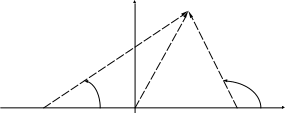
. Поле двух тонких заряженных нитей. Для двух заряженных нитей с зарядами 1 и 2, расположенных в точках с координатами z10 и z20 запишем выражение для комплексного потенциала, воспользовавшись принципом наложения:
W (z) = jA1 ln (z–z10) + jA2 ln (z–z20) + C1 + j C2.
Здесь C1 и C2 – произвольные постоянные, зависящие от выбора места расположения начальных (нулевых) линий функции потока и потенциала.
Учитывая,
что
;
и принимая, что на нитях расположены
равные по величине и противоположные
по знаку заряды (1
= – 2 = )
, получим:
Обозначим расстояние между заряженными осями через (2b). Поместим начало координат посредине между заряженными нитями (рис. 3–7), и направим ось x через центры нитей. В этом случае: z10 = – b ; z20 = + b.
y
r1 r2
z1 = (z + b) z z2 = (z – b)
1 2
x
– b 0 + b
Рисунок 3–7
Комплексный потенциал в произвольной точке имеет вид:
Записав
числитель и знаменатель подлогарифмического
выражения в полярной системе координат z1
= z + b
= r1
;
z2 =
z – b
= r2
,
получим:
;
=
V + j
U;
; 
.
Для построения линий равного потенциала (U = const) можем записать:
,
что означает: 
V1 V2 V3 V4 V5
y U1
U2
U3
U4
U5
x
Рисунок 3–4