Индуктивность трехфазной линии.

Векторный потенциал в системе из трех проводов с параллельными и одинаково направленными токами в любой точке равен:

,

причем сумма всех токов равна нулю (i₁+ i₂+i₃= 0) даже при отсутствии симметрии в системе токов.

Векторный потенциал в различных точках около проводов имеет различную начальную фазу. В связи с этим магнитные потоки, сцепленные с отдельными проводами трехфазной линии, не совпадают по фазе с токами в этих проводах, что приводит к перераспределению нагрузки между проводами и к переносу мощности между ними.

Покажем это, рассматривая уравнения трехфазной линии в комплексной форме:

.

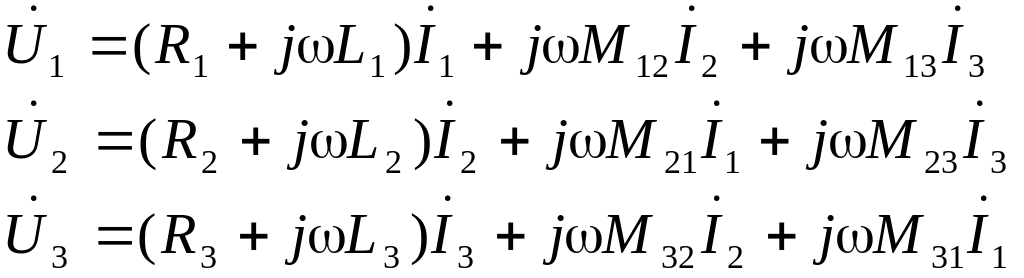
В симметричной системе токов прямой последовательности токи сдвинуты на 120⁰:

; ; ,

Учитывая симметрию системы токов: ; , получим:

I₁

.

I₃ I₂

Вещественные слагаемые в скобках различны, что свидетельствует о различных значениях активной мощности, потребляемой в разных проводах линии.

При использовании транспозиции проводов трехфазная линия становится симметричной, потому: M₁₂ = M₁₃ = M₂₃ = M, L₁ = L₂ = L₃ = L и R ₁ = R ₂ = R ₃ = R. В этом случае уравнения для различных фаз становятся идентичными:

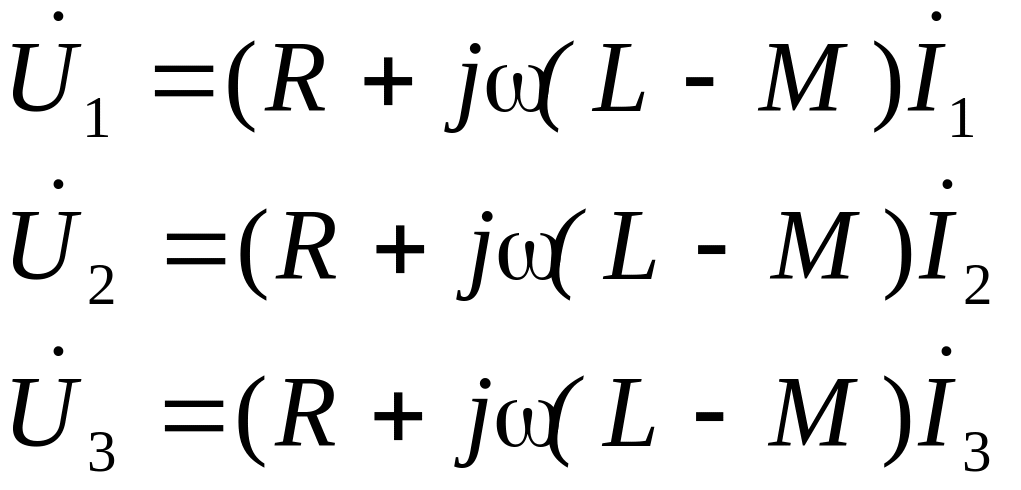
В любом проводе сдвиг фаз между током и напряжением одинаков, что позволяет исключить перенос мощности между проводами линии.

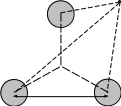
Рассмотрим трехфазную линию, провода которой расположены в вершинах равностороннего треугольника (рис.10–8): При таком расположении проводов линия симметрична без их транспозиции, если вблизи нет ферромагнитных поверхностей.

1 r₁ m

r₃ r₂

r₀

r₀ r₀

D

2 3

Рисунок 10–8

В рассматриваемой системе векторный потенциал равен нулю в бесконечности (при r_k -> ) и в центре симметрии ( r_k = r₀), так как сумма токов в скобках равна нулю:

Векторный потенциал на поверхности провода первой фазы, учитывая симметрию системы токов (i₂ + i₃ = – i₁), равен:

.

Определим внешний магнитный поток первой фазы, а затем индуктивность первой фазы, равную (из-за симметрии системы) индуктивности любой фазы:

; .