7

Лекция 10 Метод участков.

Если разбить тонкие контуры на отдельные участки (рис. 10–1а), то взаимную индуктивность между тонкими контурами можно записать в виде суммы интегралов по участкам:

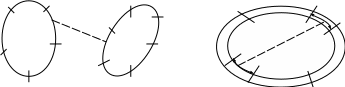
l_1k

l_1k r 1 2 r

l_2p

l_2p

а) б)

Рисунок 10–1

,

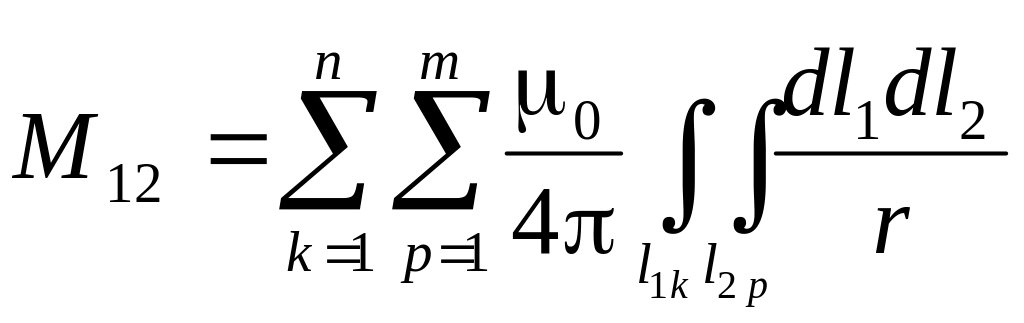Выражение, полученное под знаком двойной суммы, можно считать взаимной индуктивностью между двумя отрезками контуров:

; .

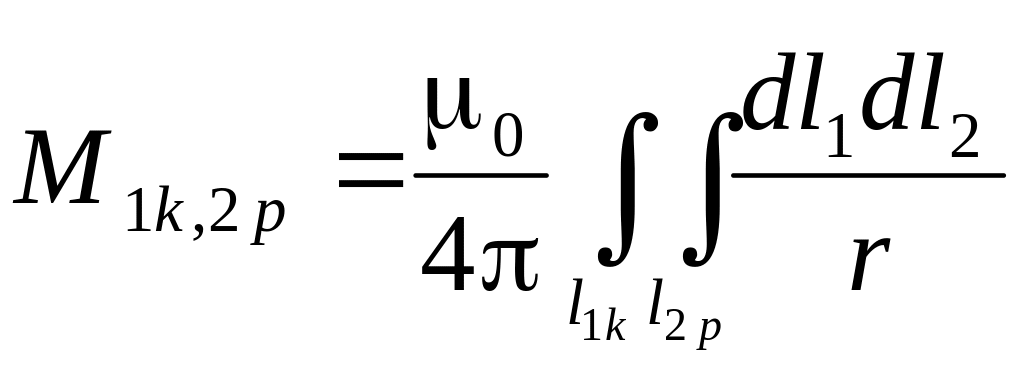Аналогично для вычисления индуктивности (рис 10–1б), учитывая, что m = n и проводя интегрирование один раз по оси, а другой по внутреннему контуру, можем записать:

.

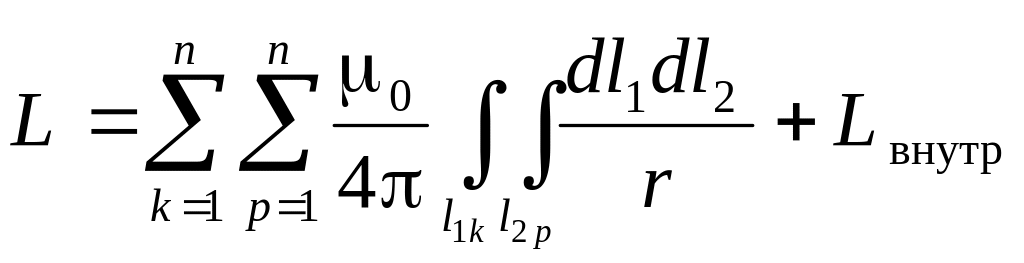Если сравнить формулы для участков, полученные для определения взаимных индуктивностей M_kp и формулы для взаимных потенциальных коэффициентов, полученные по методу средних потенциалов, то можно заметить их сходство:

; .

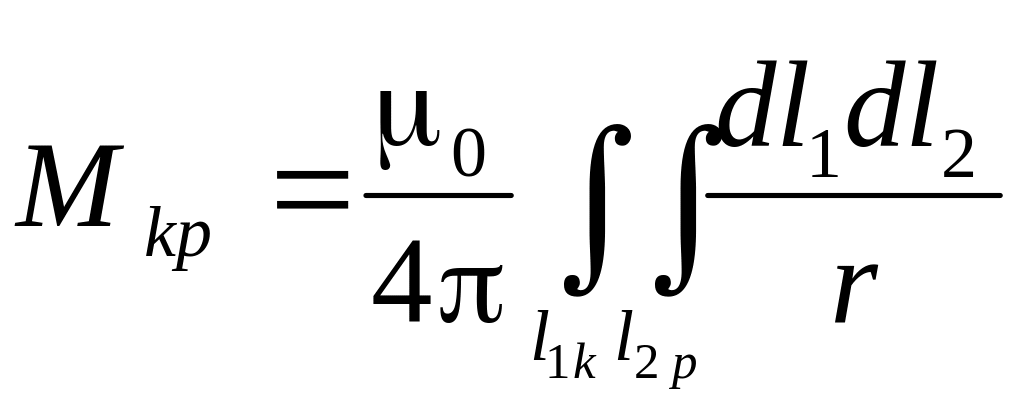Разница заключается в множителях, стоящих перед интегралами, а также в том, что при вычислении взаимной индуктивности под интегралом определяется скалярное произведение векторов элементарных отрезков: , а при вычислении взаимного потенциального коэффициента произведение модулей этих же величин (без необходимости учета косинуса угла  между ними).

Индуктивность контуров, составленных из прямолинейных отрезков.

Если отрезки прямолинейны, то cos может быть вынесен за знак интеграла, так как на всем интервале интегрирования угол  между прямолинейными отрезками остается постоянным. В этом случае выражение для взаимной индуктивности между двумя прямолинейными отрезками принимает вид:

.

Тогда для расчета взаимной индуктивности между прямолинейными отрезками можно пользоваться формулами, полученными для взаимных потенциальных коэффициентов таких же отрезков по методу средних потенциалов, используя для пересчета соотношение:

Для собственной внешней индуктивности прямолинейного отрезка, учитывая, что  = 0 и cos = 1, можем записать:

.

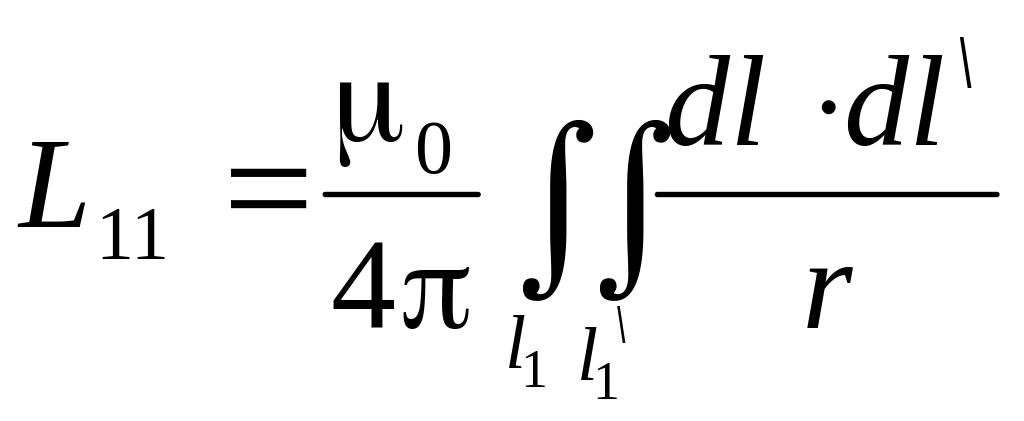Сравнивая это выражение с собственным потенциальным коэффициентом, найденным по методу средних потенциалов:

,

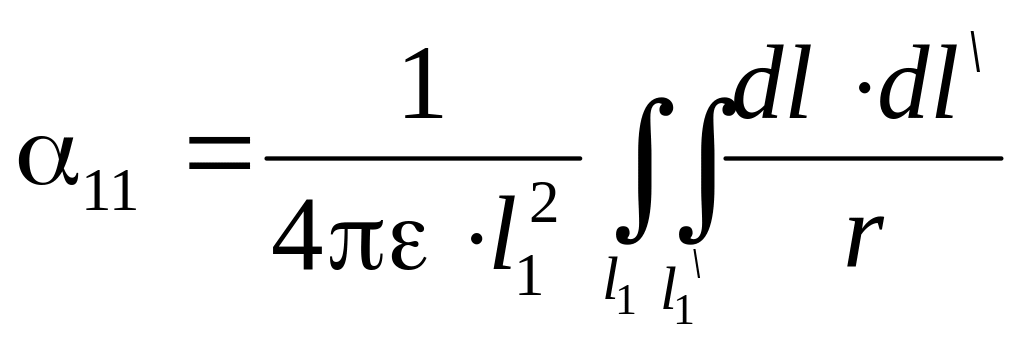легко показать, что соотношения отличаются только коэффициентами, стоящими перед интегралом, поэтому:

.

Следует подчеркнуть, что выражения для потенциальных коэффициентов, полученные по методу средних потенциалов, не позволяют обеспечить достаточно высокую точность из-за необоснованного предположения о равномерном распределении заряда вдоль отрезков проводников ( = const). Однако, аналогичные выражения для расчета индуктивностей по методу участков абсолютно точны, так как ток в проводнике во всех его сечениях одинаков (i = const).

Кроме того, необходимо иметь в виду, что дополнительный сомножитель (cos) , связывающий выражения для взаимных индуктивностей и взаимных потенциальных коэффициентов оказывает существенное влияние на результат. Если прямолинейные отрезки параллельны и направления токов в них совпадают, то cos = 1. Если токи направлены противоположно, то cos = – 1, а если отрезки перпендикулярны, то cos = 0, и взаимная индуктивность между ними будет равна нулю, хотя взаимный потенциальный коэффициент нулю не равен.

Определим в качестве примера взаимную индуктивность между двумя одинаковыми прямоугольными рамками, расположенными в параллельных плоскостях на некотором расстоянии x друг от друга (рис.10–2). Выберем направление обхода обоих контуров по часовой стрелке. При расчете взаимной индуктивности между первым и вторым контуром, разобьем каждый из них на четыре прямолинейных участка.

Определим взаимные индуктивности между всеми отрезками обоих контуров и сложим их. Таких слагаемых будет 16. Половина их этих слагаемых равна нулю из-за взаимной перпендикулярности отдельных отрезков (1a  2b, 2d; 1b  2a, 2c и т. д.). Остальные пары отрезков параллельны ( = 0⁰, 1a  2a; 1b  2b и т.д.) или антипараллельны ( = 180⁰, 1a  2c; 1b  2d и т.д.⁾ Взаимная индуктивность между этими отрезками зависит от их длины (вертикальная сторона рамки равна «a», а горизонтальная сторона рамки равна «b») и от расстояния между ними. Расстояние между параллельными отрезками равно x, а между антипараллельными определяется из соотношений и .

1b 2b

1c 2c

1a 1d 2a 2d

x

Рисунок 10–2

Для двух параллельных отрезков одинаковой длины, начало которых расположено на одном перпендикуляре к ним (рис. 10–3) можно определить взаимный потенциальный коэффициент или взаимную индуктивность:

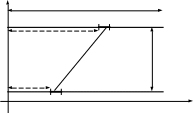l

dx₁

x₁

r D

x₂ dx₂

x

Рисунок 10–3

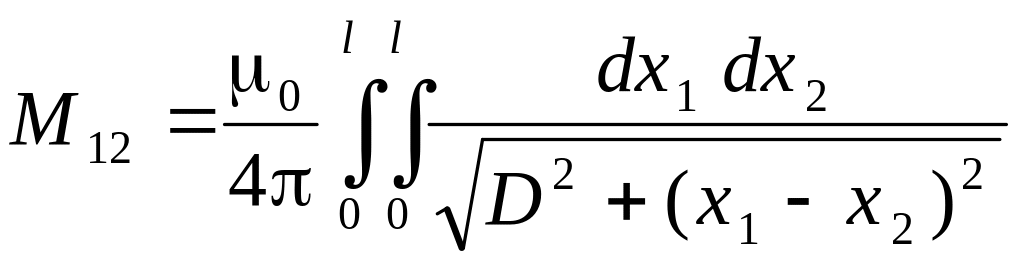
Вычисление подобных интегралов приведено в справочной литературе по расчету емкостей и индуктивностей (Иоссель; Калантаров и Цейтлин).