Добавил:

pro100durachok Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Санкт-Петербургский политехнический университет Петра Великого (бывш. СПбГПУ)

Предмет:

Высшая математика

Файл:

Криволинейные интегралы - теория

.pdf

Скачиваний:

Добавлен:

22.04.2021

Размер:

744.21 Кб

Скачать

☆

1 / 31 2 3 > Следующая >>>

Глава 2. Криволинейные интегралы

В главе 1 были рассмотрены кратные интегралы. В этой главе мы остановимся на новых разновидностях интеграла: криволинейных интегралах 1 и 2 рода. Из самого названия следует, что эти интегралы рассматриваются вдоль «кривых линий».

Под «кривой линией» (или просто кривой, или просто линией) на плоскости или в пространстве подразумевается непрерывная спрямляемая кривая без самопересечений. Такие кривые будем называть простыми кривыми. Заметим, что как частный случай, кривая может быть и отрезком прямой линии.

Спрямляемость означает, что кривая имеет конечную длину (см. [4], . ). Если кривая – замкнутая, то она называется контуром.

Изучение криволинейных интегралов начнем с интегралов 1 рода.

2.1. Криволинейный интеграл 1 рода

Здесь, как и в случае кратных интегралов, сначала введем новое понятие и изучим его свойства, затем выведем формулу для вычисления и в заключение рассмотрим некоторые его приложения.

2.1.1. Понятие криволинейного интеграла 1 рода

Рассмотрим простую кривую

на плоскости или в пространстве. Пусть на этой

кривой задана некоторая функция ( ).

−2

−1

Выполним следующие действия.

Разбиение кривой на частичные дуги

точками

≡ ,

, …, ,

≡ :

−1

(рис. 2.1),

…

- дуга

(

= 1, 2, … ,

где

−1

Выбор промежуточных точек:

= 1, 2, … , .

Рис. 2.1. Разбиение кривой

Вычисление суммы:

∑

(

) ∙ ∆

где ∆

= 1, 2, … , .

= | |

- длина частичной дуги ,

Сумма

называется интегральной суммой Римана функции ( ) по кривой .

Пусть λ =

∆ - наибольшая из длин частичных дуг - ранг разбиения.

1≤ ≤

Определение 2.1.

Число называется пределом интегральных сумм при λ → 0, если для > 0

> 0 такое, что для любого разбиения кривой с рангом разбиения λ < и при

любом выборе промежуточных точек {

}

выполняется неравенство:

− |

< .

Запись:

- означает, что при λ → 0 этот предел существует, он не

λ → 0

зависит ни от способа разбиения, ни от выбора промежуточных точек, и равен числу .

Определение 2.2.

Конечный предел интегральных сумм при λ → 0 называется криволинейным интегралом 1 рода (или криволинейным интегралом по длине дуги) от функции ( ) вдоль кривой .

Обозначения: ∫

( )

или: ∫

( , ) ,

∫ ( , , ) .

Встречаются также обозначения: ∫

( ) или: ∫ ( , ) ,

∫

( , , ) .

Таким образом, по определению имеем:

∫

( ) =

∑

(

) ∙ ∆

или:

λ → 0

∫

( , ) =

∑

( , ) ∙ ∆

- для плоской кривой

λ → 0

∫

( , , ) = ∑

(

)

∙ ∆

- для пространственной кривой.

λ → 0

Функция ( ), для которой существует криволинейный интеграл 1 рода, называется интегрируемой вдоль кривой .

Пример 2.1.

	∫	0∙ =	∑=1		0∙∆		= 0 = 0	∫ 0∙ = 0;
			λ → 0				λ → 0
			λ → 0				λ → 0
∫	1∙ =	∑=1		1∙∆ =			\| \| = \| \|	∫ 1∙ = \| \| - длина кривой .
		λ → 0				λ → 0
		λ → 0				λ → 0

Физический смысл криволинейного интеграла 1 рода.

Если ( , , ) – линейная плотность массы, распределенной вдоль кривой , то

= ∫	( , , ) – масса неоднородной кривой ;
если ( , , ) – линейная плотность электрического заряда, распределенного
вдоль кривой , то
= ∫	(, , – заряд всей кривой .
	)

Замечание 2.1.

Из определения криволинейного интеграла 1 рода вытекает следующее свойство:

∫̆	( ) = ∫̆ ( ) ,

т.е. величина интеграла не зависит от направления, выбранного на кривой . Условия интегрируемости.

Сформулируем теоремы об условиях интегрируемости функции вдоль кривой. Доказательства этих утверждений аналогичны случаю кратных интегралов.

Теорема 2.1 (Необходимое условие интегрируемости).

Если функция ( ) интегрируема вдоль кривой, то она ограничена на этой кривой.

Замечание 2.2.

Обратное утверждение неверно: есть ограниченные, но не интегрируемые функции. Теорема 2.2 (Достаточное условие интегрируемости).

Пусть - гладкая кривая (см. [4], . ), а функция ( ) непрерывна на ней. Тогда эта функция интегрируема вдоль кривой .

2.1.2. Свойства криволинейного интеграла 1 рода 1. Нормированность.

Криволинейный интеграл 1 рода от единицы вдоль кривой равен длине кривой:

∫ 1∙ = | |.

2. Линейность.

Пусть функции ( ) и ( ) интегрируемы вдоль кривой . Тогда а) постоянный множитель можно выносить за знак криволинейного интеграла 1 рода:

∫ ∙( ) = ∙∫ ( ) , = ;

б) криволинейный интеграл 1 рода от суммы функций равен сумме криволинейных интегралов 1 рода от этих функций:

∫ ( ( ) + ( )) = ∫ ( ) + ∫ ( ) .

Свойство линейности можно записать в следующем виде:

∫ (1 ∙ ( ) + 2 ∙ ( )) = 1∙∫

( ) + 2∙∫

( )

1, 2 = .

3. Аддитивность.

Пусть функция ( ) интегрируема вдоль кривой . Если кривая разбита на две дуги, то криволинейный интеграл 1 рода по всей кривой равен сумме криволинейных интегралов 1 рода по каждой из этих дуг:

∫	( ) = ∫	( ) + ∫	( ) ,	где = 1 2	и 1 ∩ 2 = .
	1	2

4. Интегрирование неравенств.

Пусть функции ( ), ( ) интегрируемы вдоль кривой и удовлетворяют неравенству: ( ) ≥ ( ) . Тогда справедливо неравенство:

∫		( ) ≥ ∫	( ) .
Следствие 2.1.
а) Если ( ) ≥ 0	, то ∫		( ) ≥ 0.
б) Пусть ( ) ≥ 0		, тогда для любых дуг 1, 2 справедливо
утверждение:
1 2		∫ ( ) ≤ ∫ ( ) .
		1	2

в) |∫ ( ) | ≤ ∫ |( )|.

5. Оценки криволинейного интеграла 1 рода.

Если значения подынтегральной функции ( ) на кривой ограничены величинами и , то значение интеграла ограничено величинами ∙| | и ∙| |, где | | - длина кривой:

≤ ( ) ≤ ∙| | ≤ ∫ ( ) ≤ ∙| |

6. Теоремы о среднем значении.

Теорема 2.3.

Пусть функция ( ) интегрируема вдоль кривой и пусть

= { ( ), };					= { ( ), }.
Тогда [ ; ]:		∫	( ) = ∙\| \|,		где \| \| - длина кривой.
Число =	1	∙∫		( ) - называется интегральным средним значением функции

	\| \|
( ) на кривой .
Теорема 2.4.
Пусть функция ( ) непрерывна на кривой . Тогда 0 :
		∫		( ) = (0)∙\| \|,		где \| \| - длина кривой.

Замечание 2.3.

Доказательство всех этих свойств аналогично случаю кратных интегралов.

2.2. Вычисление криволинейного интеграла 1 рода

Покажем, как вычисление криволинейного интеграла 1 рода ∫ ( , , ) сводится к вычислению определенного интеграла.

2.2.1. Сведе́ние к определенному интегралу

̆
На кривой = введем так называемую естественную параметризацию. Это
значит, что положение произвольной точки на кривой определяется длиной дуги
̆	(рис. 2.2). Тогда кривая будет задана
= \| \|, отсчитываемой от начальной точки	(рис. 2.2). Тогда кривая будет задана
параметрическими уравнениями:
= ( )
= ( )
{ = ( ), 0 ≤ ≤ \| \|,
{ = ( ), 0 ≤ ≤ \| \|,
= ( )
где параметр (длина дуги) называется
где параметр (длина дуги) называется
естественным параметром кривой .
При этом подынтегральная функция
( , , ) сведется к сложной функции:	0

( ( ), ( ), ( )).

По определению имеем:

∫

( , , ) =

∑

( )∙∆

Рис. 2.2. Иллюстрация к естественной

λ → 0

параметризации кривой

Здесь - промежуточная точка на дуге

= (

), где

и - точки деления кривой ,

∆

−

= ∆ -

−1

= | | =

−1

Промежуточная точка

(

, , ) соответствует

длина дуги , = 1, 2, … , .

некоторому значению естественного параметра = ,

= 1, 2, … , .

Введем обозначение: ( ) = ( ( ), ( ), ( )). Тогда интегральная сумма Римана

запишется в виде:

= ∑

(

)∙∆

= ∑

( (

), (

))∙∆ =

∑

(

)∙∆ .

Следовательно, имеем:

∫

( , , ) =

∑

(

)∙∆ .

λ → 0

Если вспомнить понятие определенного интеграла (см. [4], . ), то можно

заметить, что последнее выражение есть не что иное, как определенный интеграл от

функции ( ) по промежутку [0, | |]:

∫| | ( ) =

∑

( )∙∆ .

λ → 0

Таким образом, получаем формулу:

∫

( , , ) = ∫0| | ( ) = ∫0| | ( ( ), ( ), ( ))

Полученная формула показывает, что вычисление криволинейного интеграла 1 рода сводится к вычислению определенного интеграла.

Однако эта формула имеет чисто теоретический интерес: при вычислениях она мало пригодна, так как задать конкретную кривую с помощью естественной параметризации удается крайне редко. Необходимо получить формулу для вычисления криволинейного интеграла 1 рода при произвольной параметризации кривой.

2.2.2. Вычисление интеграла вдоль пространственной кривой

Рассмотрим гладкую кривую , заданную параметрическими уравнениями:

= ( )

{ = ( ), [ ; ], где ( ), ( ), ( ) - непрерывно-дифференцируемые функции.

= ( )

Для дальнейших выкладок нам потребуется формула для длины кривой. Как известно (см. [4], . ), длина кривой вычисляется по формуле:


		\| \| = ∫ √( ′)2 + ( ′)2 + ( ′)2			.
			̆				- имеем:
Соответственно, для длины дуги = \| \|, где ( ( ), ( ), ( ))							- имеем:
	= ( ) = ∫ √( ′)2 + ( ′)2 + ( ′)2			,		≤ ≤ .
При этом производная функции ( ) равна:

′( ) = √( ′( ))2 + ( ′( ))2 + ( ′( ))2 > 0			[ ; ], что обеспечивает строгое

возрастание функции ( ).

Теорема 2.5.

Пусть - гладкая кривая - задана параметрическими уравнениями:

= ( )

{ = ( ), [ ; ]; пусть функция ( , , ) непрерывна на кривой .

= ( )

Тогда справедлива формула:

∫

( , , ) = ∫ ( ( ), ( ), ( )) ∙ √( ′)2 + ( ′)2 + ( ′)2

Доказательство.
В пункте 2.2.1 получена формула: ∫	( , , ) = ∫0\| \| ( ( ), ( ), ( )) .

Сделаем замену переменной в этом определенном интеграле:

= ( ) = ′( ) = √( ′)2 + ( ′)2 + ( ′)2 [ ( ) = ( ( )) = ( ), ( ) = ( ( )) = ( ), ( ) = ( ( )) = ( )]

0 ≤ ≤ | | ≤ ≤

∫0| | ( ( ), ( ), ( )) = ∫ ( ( ), ( ), ( ))√( ′)2 + ( ′)2 + ( ′)2 .

Теорема доказана.

Пример 2.2.

Вычислить криволинейный интеграл 1 рода = ∫ , где - коническая

			= ∙
винтовая линия (винтовая линия на конусе):			{ = ∙ , [0; √2].
			=
Решение.
	= ∙ ,		= ∙ , =
∫ = [	′( ) = − ∙ ,	′( ) = + ∙ ,		′( ) = 1
∫ = [				] =

= √( ′)2 + ( ′)2 + ( ′)2 = √2 + 2

= ∫0√2 ∙√2 + 2 = 12 ∫0√2 √2 + 2 (2 + 2) = 13 √(2 + 2)3|√02 = 13 (8 − 2√2) = 23 (4 − √2). Ответ: = 23 (4 − √2).

2.2.3. Вычисление интеграла вдоль плоской кривой

= ( )

Вслучае плоской кривой , заданной параметрическими уравнениями: { = ( ),

[ ; ] - имеем следующую формулу для вычисления криволинейного интеграла 1 рода:

∫ ( , ) = ∫ ( ( ), ( ))∙√( ′)2 + ( ′)2 .

Если кривая задана явным уравнением: = ( ), [ ; ] - то формула принимает вид:

∫ ( , ) = ∫ ( , ( ))∙√1 + ( ′( ))2 .

Если кривая задана уравнением в полярных координатах: = ( ), [ ; ] - то формула примет вид:

∫ ( , ) = ∫ [ ( ) , ( ) ]∙√ 2 + ( ′ )2 .

Эти формулы являются следствием формул длины плоской кривой при различных способах задания этой кривой ([4], . ):

| | = ∫

| | = ∫ √1 + ( ′( ))2

| | = ∫ √ 2

+ ( ′ )2

√

( ′)2 + ( ′)2

Пример 2.3.

Вычислить криволинейный интеграл 1 рода = ∫

где – отрезок прямой,

соединяющей точки (1; 1)

и (2; 3).

Решение.

Уравнение отрезка прямой линии , проходящей через две заданные точки (1; 1) и

(2; 3) имеет вид (рис. 2.3):

= 2 − 1, [1; 2].

Применим формулу:

∫ ( , ) = ∫ ( , ( ))∙√1 + ( ′( ))2 ,

где = ( ) = 2 − 1,

′( ) = 2.

2 1

(

′)2

∫ =

∫1 ∙√1 +

= ∫1 (2 −1)∙√5 =

= √5∙∫1

= √5∙∫1 (

−

) =

(2 −1)

2 −1

∙ (

2 −1

) |2

= √5

= √5∙(

− 1) = √5

∙ 1,5.

Рис. 2.3. Иллюстрация

к Примеру 2.3

Ответ:

= √5∙ 1,5.

2.3. Приложения криволинейного интеграла 1 рода

Физические приложения

Масса кривой:

= ∫ ( , , ) - для пространственной кривой,

= ∫ ( , ) - для плоской кривой,

где ( , , ) или ( , ) - линейная плотность массы, распределенной вдоль кривой .

Электрический заряд кривой:

= ∫	(, , ) - для пространственной кривой,
= ∫	(, ) - для плоской кривой,

где ( , , ) или ( , ) - линейная плотность заряда, распределенного вдоль кривой .

Геометрические приложения

Длина кривой: \| \| = ∫	1∙ .
Длина кривой: \| \| = ∫	1∙ .
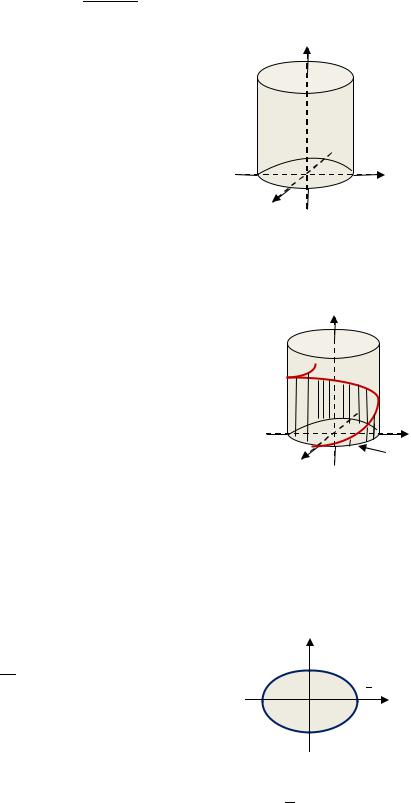
Площадь цилиндрической поверхности:
(цил.) = ∫ ( ) =	∫ ( , ) .		= ( , )
(цил.) = ∫ ( ) =	∫ ( , ) .

Здесь цилиндрическая поверхность цил.
(рис. 2.4) задается условиями:
- образующая параллельна оси ;
- направляющей служит кривая , лежащая				цил.
- направляющей служит кривая , лежащая
в плоскости ;
в плоскости ;
- сверху поверхность ограничена кривой:
- сверху поверхность ограничена кривой:
= ( , )		Рис. 2.4. Площадь цилиндрической
{ ( , ) .			поверхности

Механические приложения

Статические моменты плоской кривой относительно координатных осей и :

= ∫	)	,	= ∫	)	.
= ∫	∙(,	,	= ∫	∙(,	.

Статические моменты пространственной кривой относительно координатных плоскостей , и :

∫

)

∫

)

∫

)

∙(, ,

Координаты центра тяжести (0, 0) - плоской кривой

и (0, 0, 0) -

пространственной кривой:

∙ ,

∙

- для плоской кривой;

∙ ,

∙

- для пространственной кривой.

Моменты инерции плоской кривой относительно осей координат , и

точки - начала координат:

∫

)

∫

)

= + = ∫ (

)

∙(, ,

∙(,

Моменты инерции пространственной кривой относительно координатных плоскостей , и , относительно координатных осей , и и относительно точки - начала координат:

= ∫

)

∫

)

= ∫

)

∙(, , ,

∙(, ,

∫ (2 + 2)(, , ) ,

∫

( 2 + 2)(, , ) ,

∫ ( 2 + 2)(, , ) ,

( + + ) =

∫

( 2 + 2 + 2)∙(, , ) .

Пример 2.4.

Найти длину одного витка винтовой линии

= ∙

[0; 2 ] (рис. 2.5).

: { = ∙ ,

= ∙

Решение.

Применим формулу: | | = ∫

1∙ ,

где = √(′)2 + (′)2 + (′)2 . Здесь имеем:

′ = −∙ ,

′

Рис. 2.5. К Примеру 2.4

= ∙ ,

= ,

= √2 + 2

В результате получим: | | = ∫02 √2 + 2

= 2∙√2 + 2

Ответ: | | = 2∙√2 + 2

Пример 2.5.

Найти площадь боковой поверхности

прямого кругового цилиндра с радиусом

основания и высотой .

Решение.

Введем систему координат так, чтобы

основание цилиндра лежало в плоскости ,

начало координат совпадало с центром круга, а ось

была параллельна образующей цилиндра (рис. 2.6).

Рис. 2.6. К Примеру 2.5

Направляющей цилиндрической поверхности

будет окружность радиуса . Ограничивающая сверху кривая имеет уравнение:

= ( , ) = , где ( , ) .

Следовательно, получаем:

(цил.) = ∫

( , ) = ∫ = ∙∫

= ∙| | = 2∙ .

Ответ: бок.

цил. = 2∙ .

Пример 2.6.

Найти площадь той части боковой поверхности

прямого кругового цилиндра, которая лежит «под»

= ∙

винтовой линией: { = ∙ sin , [0; 2 ] (рис. 2.7).

= ∙

Рис. 2.7. К Примеру 2.6

Решение.

= ∙

( , ) = [ = ∙ sin ] = ∫02 ∙ √

(цил.) = ∫

(′)2

+ (′)2

= ∙

= ∫0 ∙ √(− ∙ sin )

+ ( ∙

= ∙ ∫0

= 2

Ответ: (

) = 22

цил.

Пример 2.7.

Найти массу эллипса 2 + 2 = 1, если

плотность массы в точке ( , ) равна (, ) = | |.

Решение.

Учитывая симметричность эллипса относительно осей координат (рис. 2.8) и четность функции | |, можно найти массу четверти эллипса и умножить результат на 4.

√2

Рис. 2.8. К Примеру 2.7

Эллипс можно задать параметрическими уравнениями: { = √2 ∙ , [0; 2 ].

Применим формулу для вычисления массы:

( , ) = ∫

= ∫

( ( ), ( ))∙√

(′)2 + (′)2

Вычислим массу первой четверти эллипса:

( ( ), ( ))∙√

(′)2 + (′)2

= ∫

( )∙√

(′)2

+ (′)2

= ∫2

																																( ) = ∫1
					∙√22 + 2																		= − ∫			√2 − 2									√2 − 2					=
		= ∫2			∙√22 + 2																		= − ∫		2	√2 − 2									√2 − 2					=
				0																				0										0
											1											) \|10 =		1				1			+		1	= 4∙(				1	) = + 2.
= (									+		1	∙ √2 − 2												1			+	1	=				1				+	1
											2
					√2																				√2			2		4
					√2																				√2			2		4	2				4			2
Ответ: = + 2.
Пример 2.8.
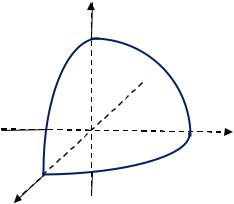
		Найти координаты центра масс контура
однородного сферического треугольника,
однородного сферического треугольника,
расположенного в первом октанте (рис. 2.9):																																2						1
	2	+	2	+			2			=			2	, ≥ 0, ≥ 0, ≥ 0.																		2
		+		+						=				, ≥ 0, ≥ 0, ≥ 0.
Решение.
		Пусть (0, 0, 0) - центр масс


заданного контура. Применим формулы:
заданного контура. Применим формулы:
		=					1		∙					=		1			∙∫ ∙(, , ) ,
							1									1
																																				3
			0																																	3

								1										1			∙∫ ∙(, , ) ,
		=						1		∙					=			1
		=								∙					=
				0

		=				1				∙					=		1			∙∫ ∙(, , ) ,												Рис. 2.9. К Примеру 2.8
		=								∙					=					∙∫ ∙(, , ) ,
			0

= ∫ ( , , ) .

Учитывая, что контур – однородный, т.е. ( , , ) = = , получаем:

= ∫

= ∙∫

= ∙| |,

∙∫

∙ =

∙ ∫

∙∫

∙| |

| |

∙∫

∙ =

∙ ∫

∙∫

∙| |

| |

∙∫

∙ =

∙

∫

∙∫

∙| |

| |

Вычислим ∫

. Разобьем контур на три кривые: = 1 2 3, где

{

2 + 2 = 2

: {

2 + 2 = 2

: {

+ 2

= 2

- четверти окружностей радиуса ;

= 0

следовательно: | | = 3∙

| |

По свойству аддитивности имеем:

∫

= ∫ 1 + ∫ 2 + ∫ 3 .

∫ 1 = ∫ 1 0 = 0;

{

= ∙

, 0 ≤ ≤

= ∙

∫ 2 = [

] = ∫0 ∙ ∙ = ∙ |0

= ;

= √(′)2 + (′)2 = ∙

= ∙

{ = ∙ ,

0 ≤ ≤ 2

∫

= [

] = ∫

∙ ∙ = 2∙ |2

= 2;

= √(′)2

+ (′)2

= ∙

∫ = 0 + 2 + 2 = 22.

Аналогично получим:

∫

= 22

и ∫

= 22.

Следовательно:

∙∫

∙22 =

| |

Ответ: (

) - центр масс.

2.4. Криволинейный интеграл 2 рода

Вначале рассмотрим задачу, которая приводит к понятию криволинейного интеграла 2 рода.

2.4.1. Задача о вычислении работы переменной силы вдоль кривой

Предположим, что материальная точка перемещается вдоль кривой под

(рис. 2.10).

действием переменной силы

Требуется найти работу , которую

при перемещении точки

( )

совершает сила

из пункта в пункт .

Частный случай этой задачи рассмотрен

в работе [4], . .

Из курса физики известно, что если

сила постоянна (по величине и направлению),

а линия = [ ] - отрезок прямой, то

работа равна скалярному произведению

вектора силы на вектор перемещения:

Рис. 2.10. Перемещение точки

= ∙ = | |∙| |∙ ,

вдоль кривой

где - угол между векторами

Для решения задачи в общем случае разобьем кривую на частичные дуги

точками ≡ , , … ,

−1

≡ :

- дуга

(

), = 1 ÷ .

…

где

−1

Далее на каждой частичной дуге выберем произвольную точку ̆ , = 1 ÷ (рис. 2.11).

Если частичные дуги имеют достаточно малые размеры, то вектор силы на этом участке можно считать постоянным и равным ( ), а дугу (−1 ) - можно считать отрезком прямой.

Тогда работа силы на этом участке приближенно равна: ≈ ( )∙∆ ,

( )

∆

−1

Рис. 2.11. Вычисление

работы на частичных дугах

где			,	= 1 ÷ .
где	∆	=	,	= 1 ÷ .
		−1
	Вся работа			равна сумме работ на частичных участках:

= ∑=1 ≈ ∑=1 ( )∙∆ .

Это приближенное равенство тем точнее, чем меньше размеры частичных дуг или модули векторов ∆ , = 1 ÷ ; другими словами, чем меньше ранг разбиения

λ = |∆ |, тем точнее эта приближенная формула.

1≤ ≤

В пределе при λ → 0 получим точное равенство:

=		∑
=		∑	=1	(	)∙∆ .
	λ → 0		=1
	λ → 0

2.4.2. Понятие криволинейного интеграла 2 рода

Пусть = ̆ - простая кривая на плоскости или в пространстве, на которой задана вектор - функция ( ), . Выберем направление на кривой, идущее от точки

к точке . Выполним следующие действия.

1. Разбиение кривой на частичные дуги точками 0 ≡ , 1, … , −1, ≡ :

1 / 31 2 3 > Следующая >>>

Соседние файлы в папке Теория и задачи

#
22.04.2021249.9 Кб10Кратные интегралы задачи.pdf
#
22.04.2021795.01 Кб7Кратные интегралы теория.pdf
#
22.04.2021218.25 Кб8Криволинейные интегралы - задачи.pdf
#
22.04.2021744.21 Кб8Криволинейные интегралы - теория.pdf
#
22.04.2021217.24 Кб7Поверхностные интегралы - задачи.pdf
#
22.04.2021758.24 Кб8Поверхностные интегралы - теория.pdf