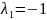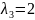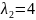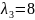Линадз1
.docxМинистерство науки и высшего образования Российской Федерации
К алужский
филиал федерального государственного
бюджетного образовательного учреждения
высшего профессионального образования
алужский
филиал федерального государственного
бюджетного образовательного учреждения
высшего профессионального образования
«Московский государственный технический университет имени Н.Э. Баумана
(Национальный Исследовательский Университет)»
(КФ МГТУ им. Н.Э. Баумана)
ФАКУЛЬТЕТ |
М-КФ «Машиностроительный» |
КАФЕДРА |
М10-КФ «Высшая математика» |
ДОМАШНЯЯ РАБОТА №1
«____________________________________»
ДИСЦИПЛИНА: |
"Линейная алгебра и ФНП" |
|
|
|
|
Выполнил: студент гр. |
_______________(Прудников А.Ф.) Подпись Ф.И.О.
|
Проверил: |
_______________(Емельянов Л.А.) Подпись Ф.И.О.
|
Дата сдачи (защиты): |
|
|
Результаты сдачи (защиты):
-Балльная оценка
-Оценка |
|
|
|
|
|
Калуга, 2020 г.
Вариант №21
Задание №1
Решить систему методом наименьших квадратов. Найти сумму квадратов невязок.
Решение:
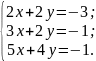
Разберем данную неоднородную СЛАУ на три матрицы:
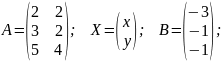
Приведем запись данной нСЛАУ в форме матричного уравнения:
AX=B
Домножим
получившееся уравнение на
 и выразим матрицу X:
и выразим матрицу X:
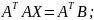
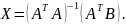
Найдем
матрицу
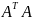 :
:
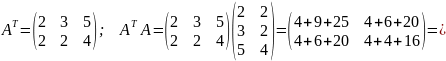
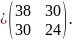
Теперь
найдём обратную матрицу
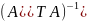 :
:
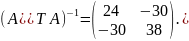
Найдём
матрицу
 :
:

Зная
и
,
найдём матрицу
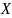 :
:
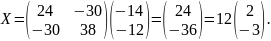
Из получившейся матрицы мы видим, что х=2, а у=-3. Теперь найдём невязки, а затем найдём квадрат суммы невязок Δ:
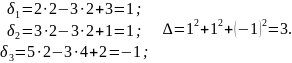
Задание №2
Решить
выражение
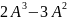 двумя способами и найти
двумя способами и найти
 ,
при
,
при
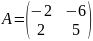 .
.
Решение:
Решим уравнение классическим методом :
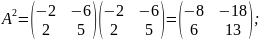
 ;
;
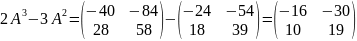 ;
;
Теперь решим методом приведения к диагональному виду:
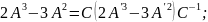
Решим
характеристическое уравнение:

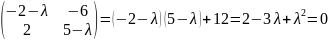 ;
;
Получившиеся
корни:

Матрицу
А
приведем к вертикальной матрице
 .
.
Найдём собственный вектор, если
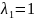 :
:
Составим систему:
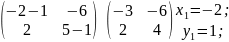
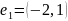 – первый
собственный вектор
– первый
собственный вектор
Найдём собственный вектор, если
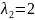 :
:
Составим систему:
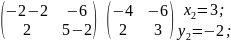
 – второй
собственный вектор.
– второй
собственный вектор.
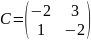 – матрица
перехода из собственных векторов
– матрица
перехода из собственных векторовНайдём обратную матрицу матрице С:
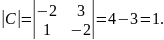
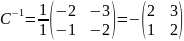
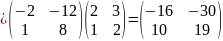 ;
;
Чтобы найти воспользуемся следующей формулой:
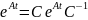 ;
;
 .
.
Задание №3
Приведите
квадратичную форму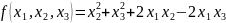 к каноническому виду. Укажите базис, в
котором квадратичная форма имеет
канонический вид.
к каноническому виду. Укажите базис, в
котором квадратичная форма имеет
канонический вид.
Решение:
-
Матрица квадратичной формы в исходном ортонормированном базисе имеет вид:

Найдем собственные значения матрицы A. Для этого решим характеристическое уравнение:
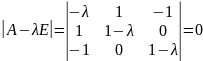 .
.
Вычисляя
определитель получаем уравнение
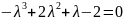 .
.
Попробуем
найти корень среди делителей свободного
члена -2.
Проверяем на корни делители:-1, 1, 2, -2.
Подставляя в уравнение
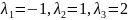 ,
убеждаемся, что это корни.
,
убеждаемся, что это корни.
Из
этого следует, что в новом ортонормированном
базисе из собственных векторов матрица
квадратичной формы примет вид
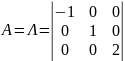 .
Следовательно, в этом базисе квадратичная
форма имеет канонический вид:
.
Следовательно, в этом базисе квадратичная
форма имеет канонический вид:
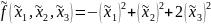
Решим систему:
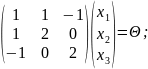
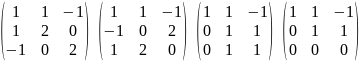
Ранг матрицы равен 2
В
качестве базисного минора берем 1-й и
2-й столбцы. Переменные
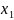 ,
,
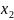 - главные,
- главные,
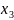 -свободная.
-свободная.
Пусть равно c. Выпишем систему:
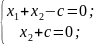
Тогда
получаем решение этой системы
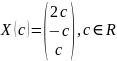 .
Это множество всех собственных векторов
для
.
Это множество всех собственных векторов
для
 .
.
В
качестве собственного вектора берем
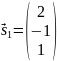 ,
при с=1.
,
при с=1.
Нормируем этот вектор:
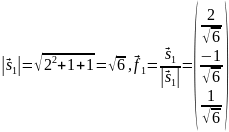 .
.
Получили
первый вектор ортонормированного базиса
 .
.
Решим систему:

Ранг матрицы равен 2.
В качестве базисного минора берем 1-й и 2-й столбцы.
Переменные и – главные, – свободная.
Пусть равно с. Выпишем систему:
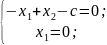
Тогда
получаем решение этой системы
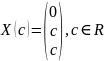 .
Это множество всех собственных векторов
для
.
.
Это множество всех собственных векторов
для
.
В
качестве собственного вектора берем
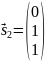 ,
при с=1.
,
при с=1.
Нормируем этот вектор:
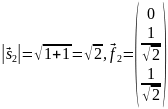 .
.
Получили
второй вектор ортонормированного базиса
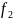 .
.
Решим систему:
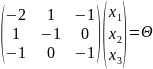 ;
;
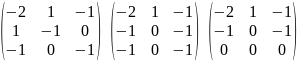 ;
;
Ранг матрицы равен 2.
В качестве базисного минора берем 1-й и 2-й столбцы.
Переменные и – главные, – свободная.
Пусть равно с. Выпишем систему:
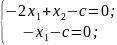
Тогда
получаем решение этой системы
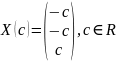 .
Это множество всех собственных векторов
для
.
.
Это множество всех собственных векторов
для
.
В
качестве собственного вектора берем
вектор
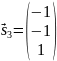 ,
при с=1.
,
при с=1.
Нормируем этот вектор:
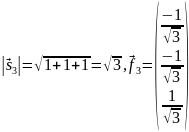 – получили
третий вектор ортонормированного базиса
.
– получили
третий вектор ортонормированного базиса
.
Задание №4
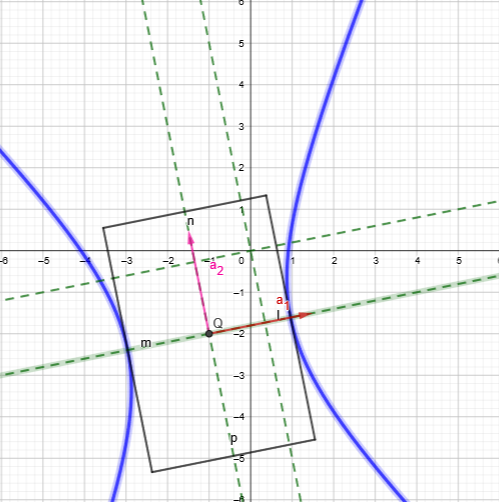
Приведите уравнение
кривой
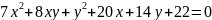 к каноническому виду. Изобразите осевой
прямоугольник и саму кривую
к каноническому виду. Изобразите осевой
прямоугольник и саму кривую
Решение:
Запишем
матрицу квадратичной части кривой
 .
.
Методом
ортогонального преобразования приведем
квадратичную форму
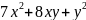 к каноническому виду.
к каноническому виду.
Найдём собственные значения матрицы А: для этого решим характеристическое уравнение
 .
Получаем корни
.
Получаем корни
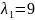 и
и
 .
.
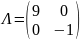 матрица
квадратичной формы базиса f
матрица
квадратичной формы базиса f
Найдём собственные векторы.
Если , то
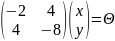 ;
;
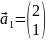 – первый
собственный вектор.
– первый
собственный вектор.
Сразу нормируем этот вектор:
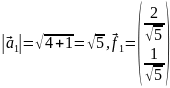 – первый
вектор ортонормированного базиса.
– первый
вектор ортонормированного базиса.
Если , то
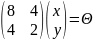 ;
;
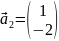 – второй
собственный вектор.
– второй
собственный вектор.
Нормируем этот вектор:
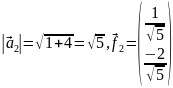 – второй
вектор ортонормированного базиса.
– второй
вектор ортонормированного базиса.
Получили
ортонормированный базис
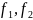 ,
в котором квадратичная форма имеет
канонический вид
,
в котором квадратичная форма имеет
канонический вид
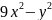 .
.
Запишем
матрицу ортогонального преобразования
координат. Эта матрица связывает старые
координаты с новыми по закону
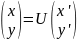 ,
или
,
или
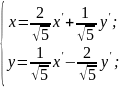
Изменение базиса привело к линейной замене переменных:
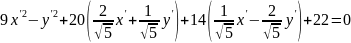
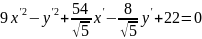 ;
;
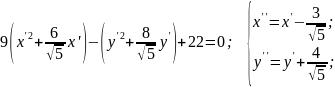
 ;
;
 – уравнение
гиперболы
– уравнение
гиперболы

Задание №3
Приведите
квадратичную форму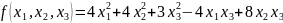 к каноническому виду. Укажите базис, в
котором квадратичная форма имеет
канонический вид.
к каноническому виду. Укажите базис, в
котором квадратичная форма имеет
канонический вид.
Решение:
-
Матрица квадратичной формы в исходном ортонормированном базисе имеет вид:

Найдем собственные значения матрицы A. Для этого решим характеристическое уравнение:
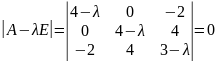 .
.
Вычисляя
определитель получаем уравнение
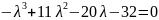 .
.
Попробуем
найти корень среди делителей свободного
члена -2.
Проверяем на корни делители:-1, 1, 2, -2, 4,
-4, 8, -8, 16, -16, 32, -32. Подставляя в уравнение
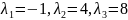 ,
убеждаемся, что это корни.
,
убеждаемся, что это корни.
Из
этого следует, что в новом ортонормированном
базисе из собственных векторов матрица
квадратичной формы примет вид
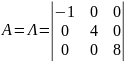 .
Следовательно, в этом базисе квадратичная
форма имеет канонический вид:
.
Следовательно, в этом базисе квадратичная
форма имеет канонический вид:
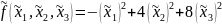
Решим систему:
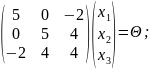

Ранг матрицы равен 2
В качестве базисного минора берем 1-й и 2-й столбцы. Переменные , - главные, -свободная.
Пусть равно c. Выпишем систему:
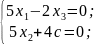
Тогда
получаем решение этой системы
 .
Это множество всех собственных векторов
для
.
.
Это множество всех собственных векторов
для
.
В
качестве собственного вектора берем
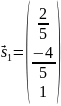 ,
при с=1.
,
при с=1.
Нормируем этот вектор:
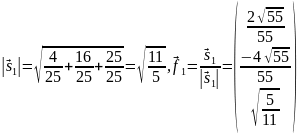 .
.
Получили первый вектор ортонормированного базиса .
Решим систему:
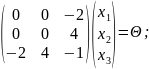
Ранг матрицы равен 2.
В качестве базисного минора берем 1-й и 2-й столбцы.
Переменные и – главные, – свободная.
Пусть равно с. Выпишем систему:
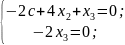
Тогда
получаем решение этой системы
 .
Это множество всех собственных векторов
для
.
.
Это множество всех собственных векторов
для
.
В
качестве собственного вектора берем
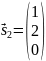 ,
при с=1.
,
при с=1.
Нормируем этот вектор:
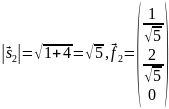 .
.
Получили второй вектор ортонормированного базиса .
Решим систему:
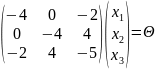 ;
;
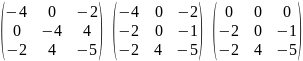 ;
;
Ранг матрицы равен 2.
В качестве базисного минора берем 1-й и 2-й столбцы.
Переменные и – главные, – свободная.
Пусть равно с. Выпишем систему:
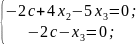
Тогда
получаем решение этой системы
 .
Это множество всех собственных векторов
для
.
.
Это множество всех собственных векторов
для
.
В
качестве собственного вектора берем
вектор
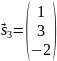 ,
при с=1.
,
при с=1.
Нормируем этот вектор:
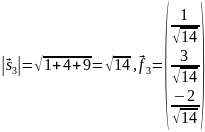 – получили
третий вектор ортонормированного базиса
.
– получили
третий вектор ортонормированного базиса
.
Задание №4
Приведите уравнение
кривой
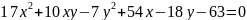 к каноническому виду. Изобразите осевой
прямоугольник и саму кривую
к каноническому виду. Изобразите осевой
прямоугольник и саму кривую
Решение:
Запишем
матрицу квадратичной части кривой
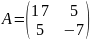 .
.
Методом ортогонального преобразования приведем квадратичную форму к каноническому виду.
Найдём собственные значения матрицы А: для этого решим характеристическое уравнение
 .
Получаем корни
.
Получаем корни
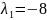 и
и
 .
.
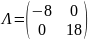 матрица
квадратичной формы базиса f
матрица
квадратичной формы базиса f
Найдём собственные векторы.
Если , то
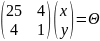 ;
;
 – первый
собственный вектор.
– первый
собственный вектор.
Сразу нормируем этот вектор:
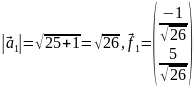 – первый
вектор ортонормированного базиса.
– первый
вектор ортонормированного базиса.
Если , то
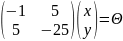 ;
;
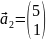 – второй
собственный вектор.
– второй
собственный вектор.
Нормируем этот вектор:
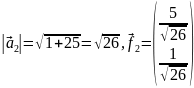 – второй
вектор ортонормированного базиса.
– второй
вектор ортонормированного базиса.
Получили
ортонормированный базис
,
в котором квадратичная форма имеет
канонический вид
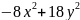 .
.
Запишем
матрицу ортогонального преобразования
координат. Эта матрица связывает старые
координаты с новыми по закону
,
или
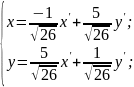
Изменение базиса привело к линейной замене переменных:
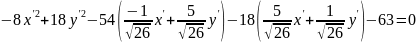
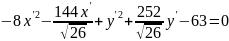 ;
;

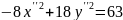 ;
;
 – уравнение
гиперболы
– уравнение
гиперболы