Линадз2
.docxМинистерство науки и высшего образования Российской Федерации
К алужский
филиал федерального государственного
бюджетного образовательного учреждения
высшего профессионального образования
алужский
филиал федерального государственного
бюджетного образовательного учреждения
высшего профессионального образования
«Московский государственный технический университет имени Н.Э. Баумана
(Национальный Исследовательский Университет)»
(КФ МГТУ им. Н.Э. Баумана)
ФАКУЛЬТЕТ |
М-КФ «Машиностроительный» |
КАФЕДРА |
М10-КФ «Высшая математика» |
ДОМАШНЯЯ РАБОТА №2
«Функции нескольких перемненных»
ДИСЦИПЛИНА: |
"Линейная алгебра и ФНП" |
|
|
|
|
Выполнил: студент гр.РПД.Б.-21 |
_______________(Прудников А.Ф.) Подпись Ф.И.О.
|
Проверил: |
_______________(Емельянов Л.А.) Подпись Ф.И.О.
|
Дата сдачи (защиты): |
|
|
Результаты сдачи (защиты):
-Балльная оценка
-Оценка |
|
|
|
|
|
Калуга, 2020 г.
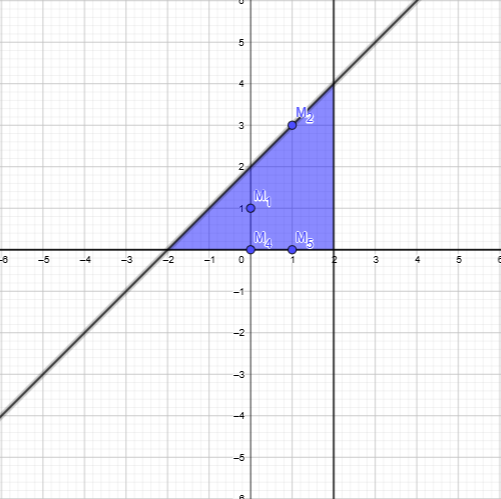
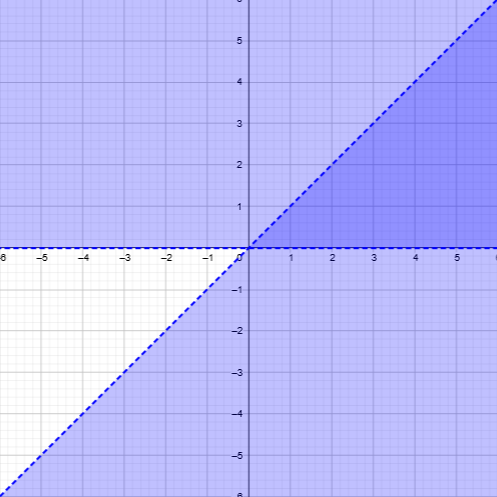
Задание №1
Найти
область определения функции и изобразить
ее на чертеже
 .
.
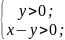
Задание №2
Вычислить
приближенно
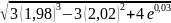 .
.


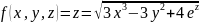

 ;
;
 ;
;
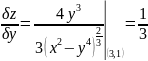 ;
;
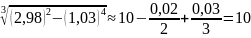 ;
;
 ;
;
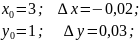
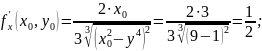


Задание №3
Проверить, удовлетворяет ли указанному уравнению данная функция Z

Найдём производные функции z:
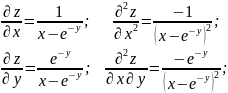
Подставим получившиеся значения в диффуравнение:
 -
верно, значит функция
-
верно, значит функция
 подходит
подходит
Задание №4
Найти уравнение касательной плоскости и нормали к заданной поверхности S в точке М0(x0,y0,z0).
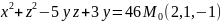
Т.к.
у нас уравнение не выраженное, то
уравнение касательной плоскости и
уравнение нормали в точке
 будут соответственно следующими:
будут соответственно следующими:
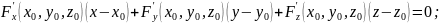

Сначала найдём производные по переменным в этой точке.



Теперь воспользовавшись формулами подставим получившиеся значения в них:
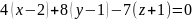 – уравнение
касательной плоскости в точке
– уравнение
касательной плоскости в точке
 .
.
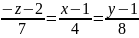 -
уравнение нормали в точке
-
уравнение нормали в точке
 .
.
Задание №5
Найти
производную функции U=f(x,y,z) в точке
 по
направлению вектора
по
направлению вектора

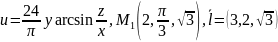
Производная
в точке
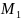 по направлению
по направлению
 находится по следующей формуле:
находится по следующей формуле:
 .
.
Сначала найдём производные по переменным:

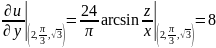
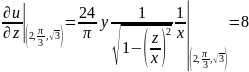
Теперь
найдём направляющие косинусы по формулам
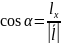 ,
,
 ,
,
 .
Для этого найдём длину вектора
:
.
Для этого найдём длину вектора
:
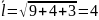 .
.
Теперь подставим в уравнения:

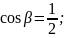

Подставим все имеющиеся значения в начальную формулу и найдём ответ:
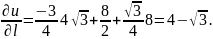
Задание №5
Исследовать
на экстремум функцию
 .
.
Решение:
Находим частные производные первого порядка:

Критические точки находятся из системы:
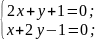
Решением
системы является точка

Находим
частные производные второго порядка
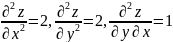 и составим дискриминант
и составим дискриминант
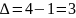 .
.
Находим значение дискриминанта в точке:
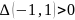 и
и
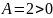 ,
следовательно в точке
функция имеет минимум,
,
следовательно в точке
функция имеет минимум,
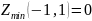 .
.
Задание №7
Найти
экстремум функции
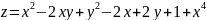
Найдём частные производные функции:
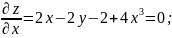
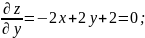
Составим и решим систему уравнений:
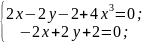
Отсюда
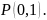
Теперь найдём частные производные второго порядка:

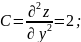

Подставим
в каждое значение точки
 :
:
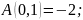
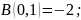

И
найдём дискриминант
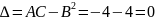 – точка перегиба.
– точка перегиба.
Задание №6
Найти наибольшее и наименьшее значение функции z=z(x,y) в области D, ограниченной заданными линиями
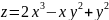 D:
x=0, x=1, y=2, y=6
D:
x=0, x=1, y=2, y=6
Исследуем
функцию на локальный экстремум и найдём
частные производные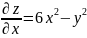 и
и
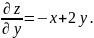
Составим и решим систему уравнений:
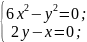
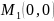 –решение
системы уравнений.
–решение
системы уравнений.
Найдём
частные производные второго порядка: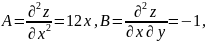
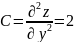 и составим дискриминант
и составим дискриминант
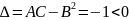 .
Следовательно, в точке
.
Следовательно, в точке
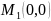 экстремума нет.
экстремума нет.
На
границе области
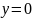 функция примет следующий вид
функция примет следующий вид
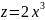 ,
при этом
,
при этом
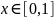 .
Исследуем функцию на экстремум. Найдём
производную
.
Исследуем функцию на экстремум. Найдём
производную
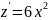 откуда точка
откуда точка
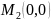 и значение функции в ней
и значение функции в ней
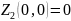 .
.
На
границе области
 функция примет следующий вид
функция примет следующий вид
 ,
при этом
,
при этом
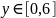 .
Исследуем функцию на экстремум. Найдём
производную
.
Исследуем функцию на экстремум. Найдём
производную
 откуда точка
откуда точка
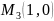 и значение функции в ней
и значение функции в ней
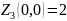 .
.
На
границе области
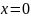 функция примет следующий вид
функция примет следующий вид
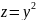 ,
при этом
.
Исследуем функцию на экстремум. Найдём
производную
,
при этом
.
Исследуем функцию на экстремум. Найдём
производную
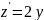 откуда точка
откуда точка
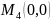 и значения функции в ней
и значения функции в ней
 .
.
На
границе области
 функция примет следующий вид
функция примет следующий вид
 ,
при этом
,
при этом
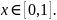 Исследуем функцию на экстремум. Найдём
производную
Исследуем функцию на экстремум. Найдём
производную
 откуда точка
откуда точка
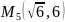 и значение функции в ней
и значение функции в ней
 .
.
Будем
иметь
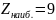 в точке
в точке
 и
и
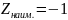 в точке
в точке
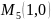 .
.