Алгоритм поиска кратчайшего пути в графе.
Клики. Алгоритм поиска клик.
Клика – некоторый подграф данного графа, являющийся полным графом, построенный на соответствующим количестве вершин.
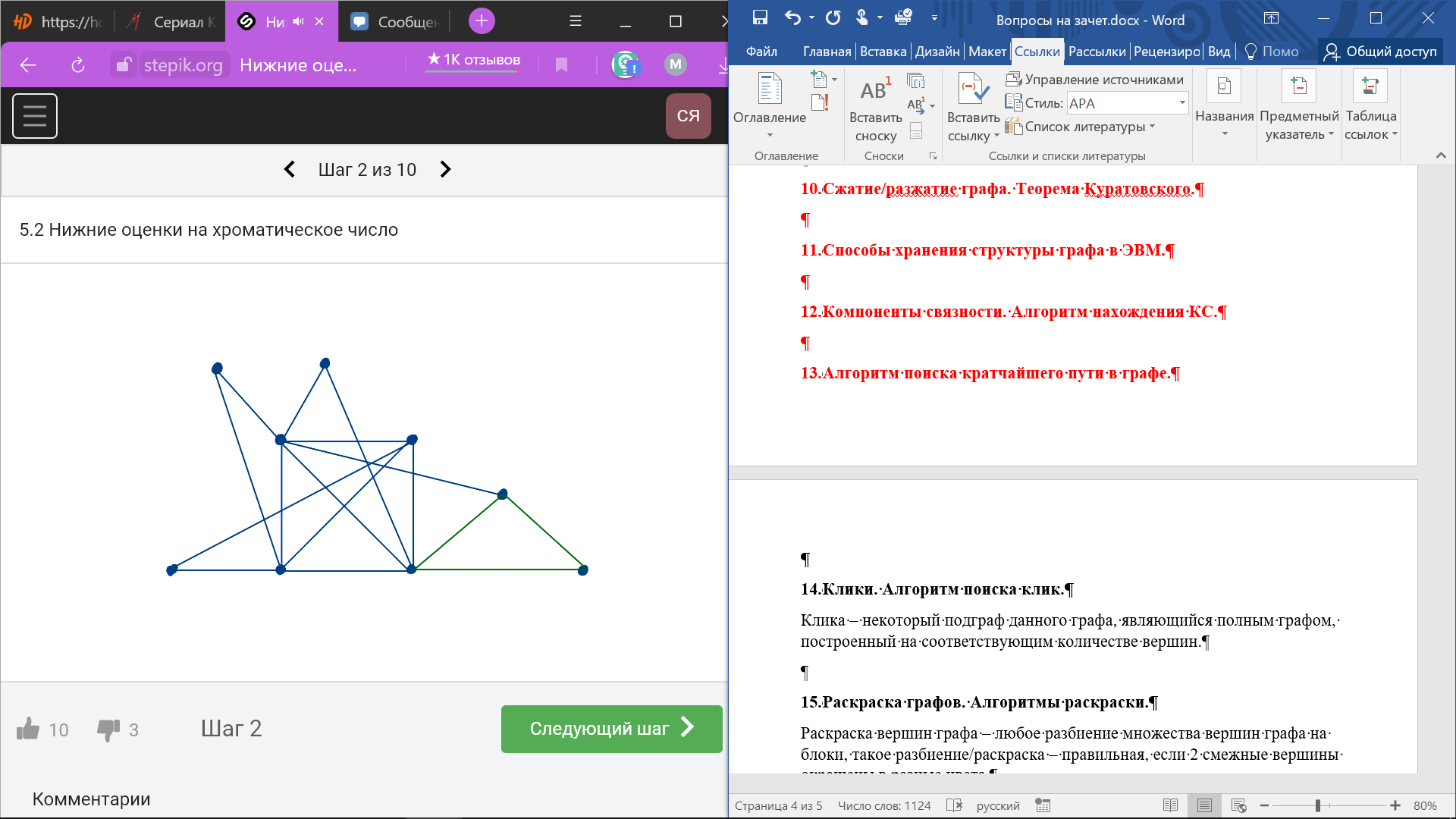клика
Кликовое число – кол-во вершин в наибольшей клике данного графа
кликовое
число = 4
Хроматическое число любого графа больше или равно кликового числа
Раскраска графов. Алгоритмы раскраски.
Раскраска вершин графа – любое разбиение множества вершин графа на блоки, такое разбиение/раскраска – правильная, если 2 смежные вершины окрашены в разные цвета.
k раскрашиваемый граф – любой граф который допускает правильную раскраску
рассматриваются только простые неориентированные графы, потому что петля по определению невозможна, нас интересует вопрос соединение двух вершин, а каким количеством рёбер значение не имеет.
Хроматическое число графа – минимальное число раскраски вершин графа
В
полном графе хроматическое число равно
кол-ву вершин
Минимально возможное число = 1, это пустой граф (1 вершина)
Двудольный
граф = 2
(от 2 точек до бесконечный цикл с чётным
количеством вершин)
Хроматическое число пустого графа = 1 (n^0)
Пример из жизни экзамены в вузе. n – кол-во предметов(вершины), ребро между вершинами – если студент сдаёт этот предмет, количество цветов – количество дней сессии
Не существует алгоритма, который нам для заданного графа гарантированно находил хроматическое число
Жадный алгоритм (самый распространённый)
Берётся произвольная вершина и смотрятся все окрашенный смежные с ней вершины, и окрашивается в цвет которого нет у вершин смежных с ней вершин.
Самый худший случай, дельта – максимальная степень вершины в графе,
Когда все смежные вершины с максимальной степенью вершины уже окрашены в разные цвета
вершина все дельта смежных с ней вершин уже окрашены, тогда эта вершина будет окрашена в дельта +1 цвет
хроматическое
число графа будет ограничено дельтой
+1
В графе любые 2 произвольных цвета можно поменять между собой
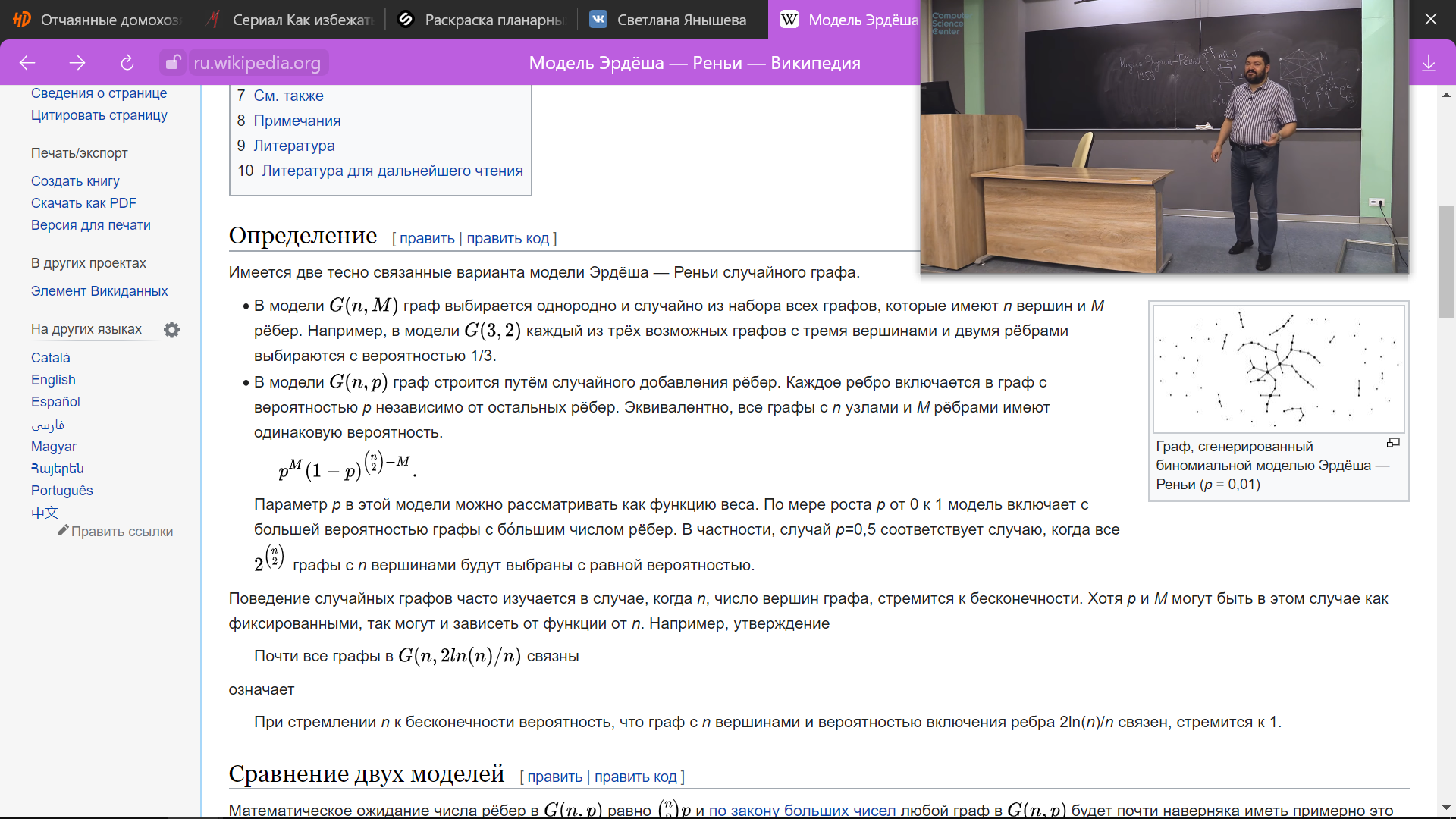
Генерация случайных графов.
