
- •Графы. Основные определения. Соотношения между количеством ребер и количеством вершин.
- •Изоморфизм графов. Примеры.
- •Пути, цепи, циклы.
- •Связность графов.
- •Эйлеров цикл. Определение, условие существования, алгоритм нахождения.
- •Гамильтонов цикл. Определение. Задача о коммивояжере.
- •Деревья.
- •ОстОвное дерево. Алгоритм Крускала.
- •Алгоритм поиска кратчайшего пути в графе.
- •Клики. Алгоритм поиска клик.
- •Раскраска графов. Алгоритмы раскраски.
- •Генерация случайных графов.
Графы. Основные определения. Соотношения между количеством ребер и количеством вершин.
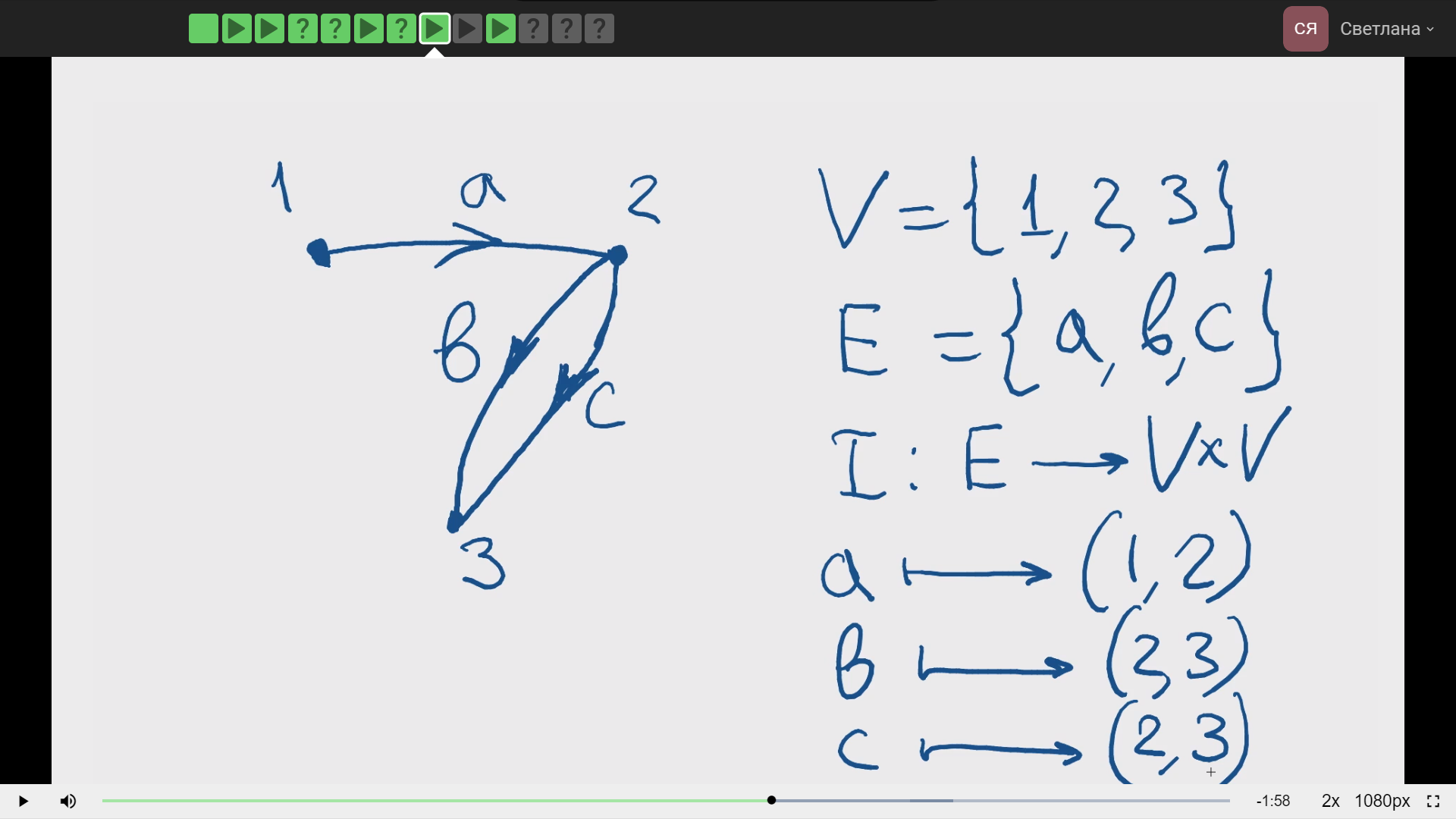
G=(V, E, I),
G – граф,
V – порядок (число вершин);
E – размер графа (число рёбер).
W – вес графа, символ(цифра) на ребре, записывается по порядку вершин
Степень вершины – количество рёбер выходящих их вершины
Простой граф - только одно ребро между вершинами и без петель. Проверяйте кол-во вершин степени вершины (невозможно при 4 вершинах иметь степень вершины больше 3-х)
входящая степень вершины 2 = 1, исходящая степень = 2
Простой граф – не имеет петель, а также если он не имеет рёбер с одинаковой упорядоченной парой вершин.
 простой
граф
простой
граф
Смежность вершин для неориентированного – вершина Y смежна с вершиной X, если в графе существует ребро соединяющее вершину Y с вершиной X.
Смежность вершин для ориентированного – вершина Y смежна с вершиной X, если в ориентированном графе существует ребро исходящее из вершины Х и входящее в вершину Y.
 вершина
Y
смежная, Х несменная
вершина
Y
смежная, Х несменная
 матрица
смежности
матрица
смежности
|
1 |
2 |
1 |
|
|
2 |
|
|
Ориентирований граф матрица смежности, из 1 в 2
 список
смежности
список
смежности
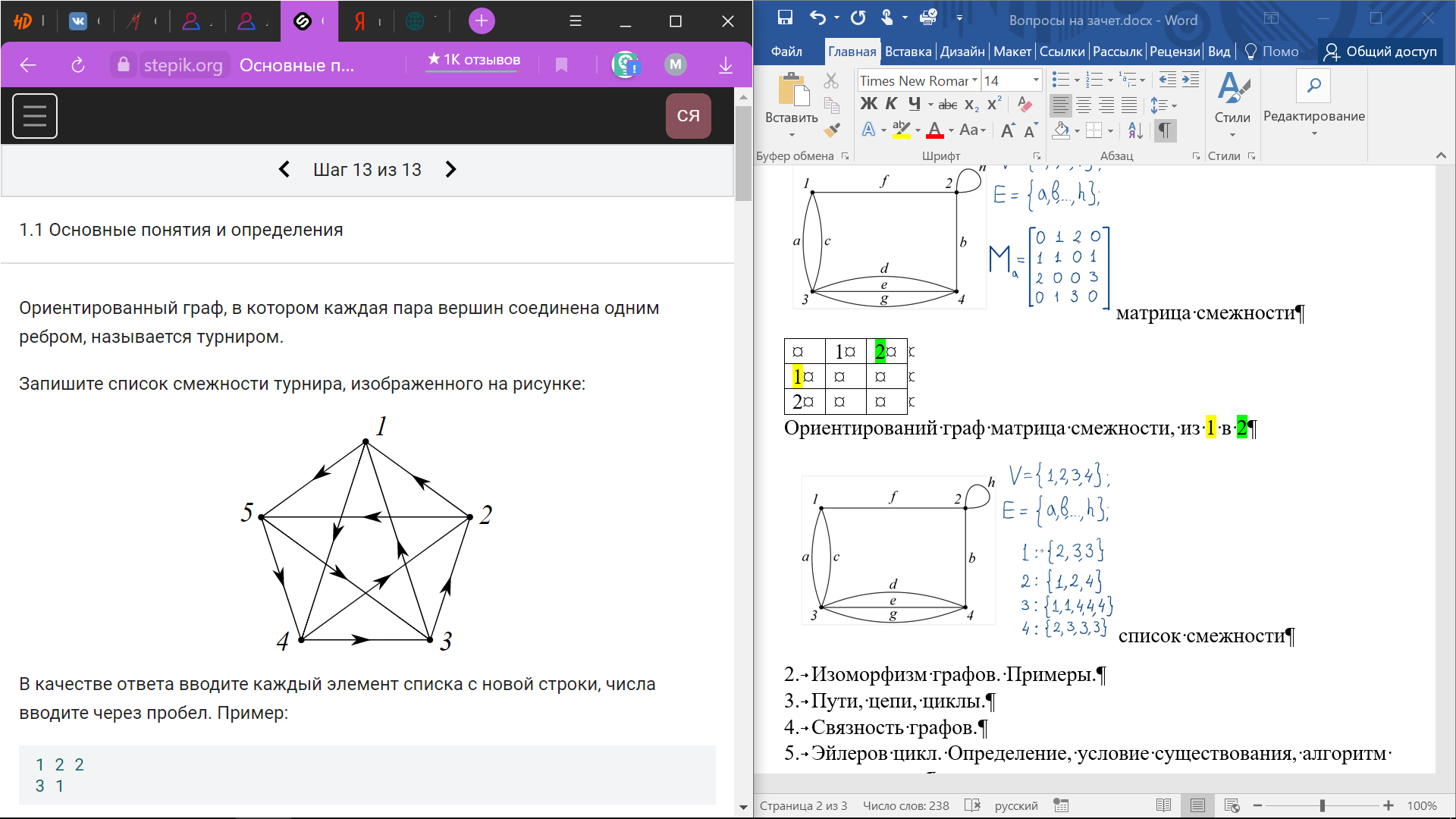 турнир
турнир
Ответ:

Полный граф – каждая вершина соеденена с каждой вершиной
Однородный граф – это граф, степени всех вершин которого
равны.
Изоморфизм графов. Примеры.
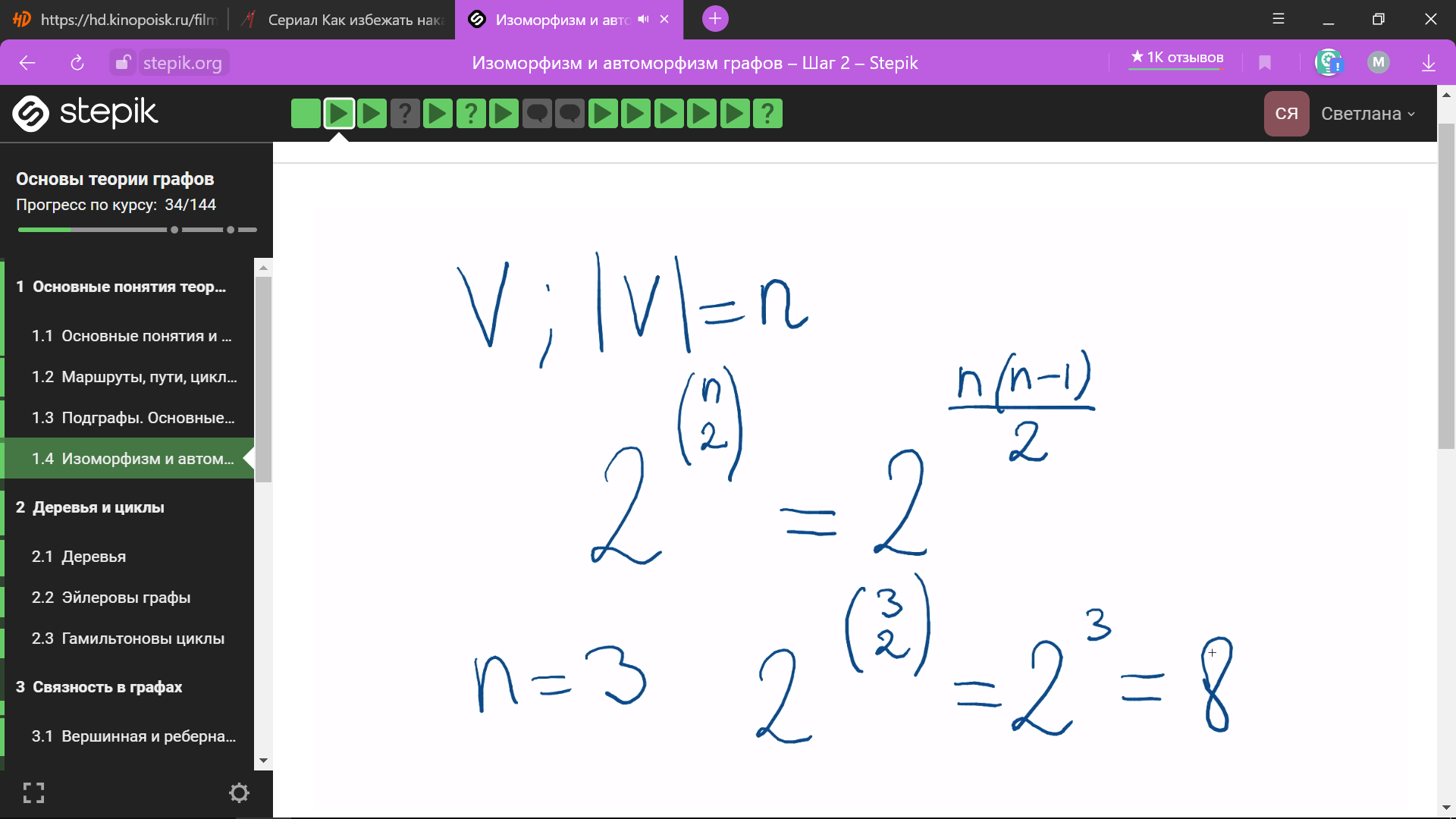
 кол-во
неориентированных простых графов
кол-во
неориентированных простых графов
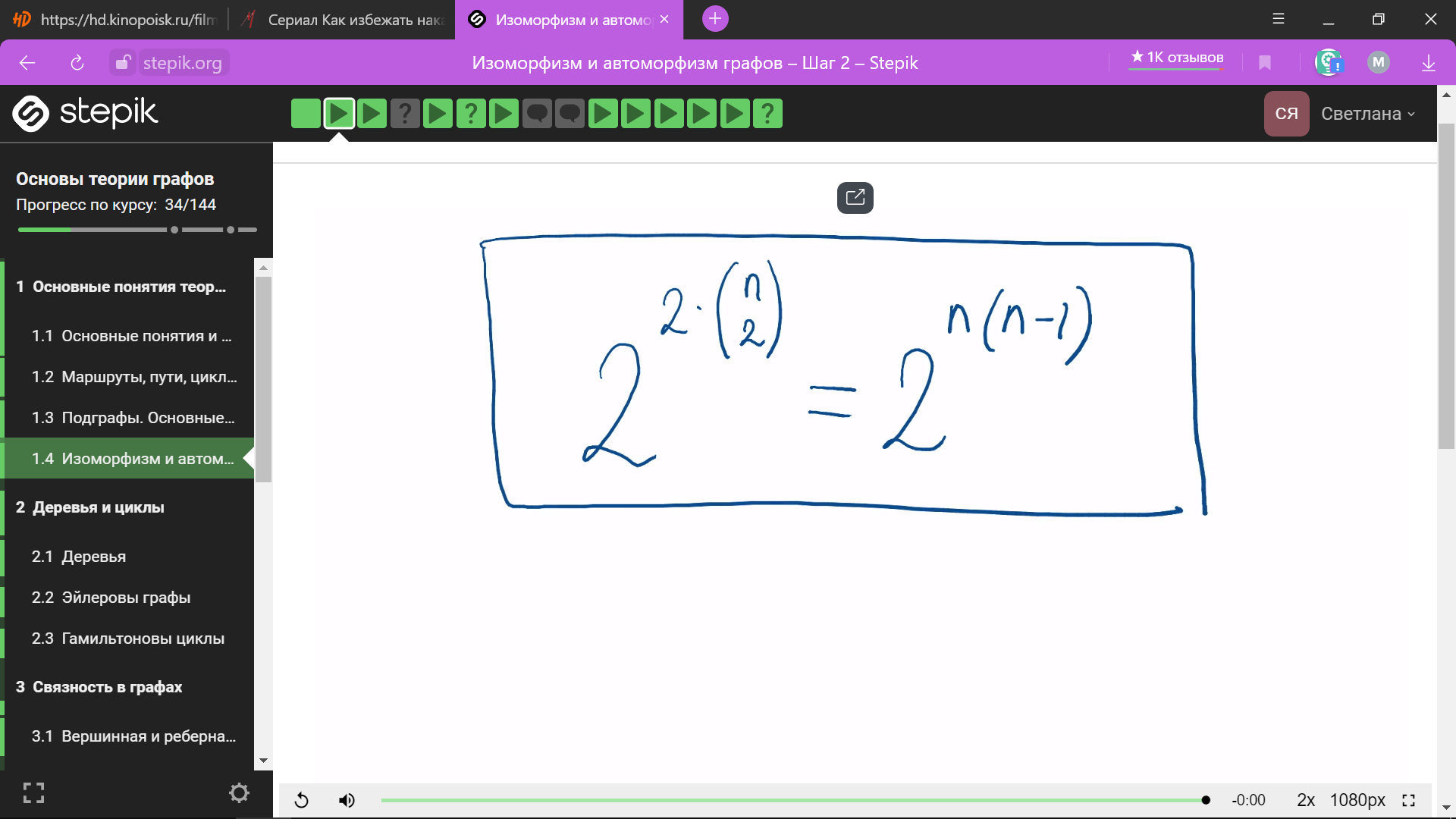 кол-во
ориентированных простых графов
кол-во
ориентированных простых графов
Изоморфизм простых графов – графы G1 и G2 изоморфны если существует отображение ФИ из множества вершин V1 в V2 которые являются взаимно однозначными и сохраняют отношение смежности (в графе G1 имеется ребро х y = Е(число рёбер) принадлежащие множеству рёбер графа G1 тогда в графе G2 обязано быть ребро фи от х и фи от у, они должны принадлежать множеству рёбер графа G2 и наоборот)
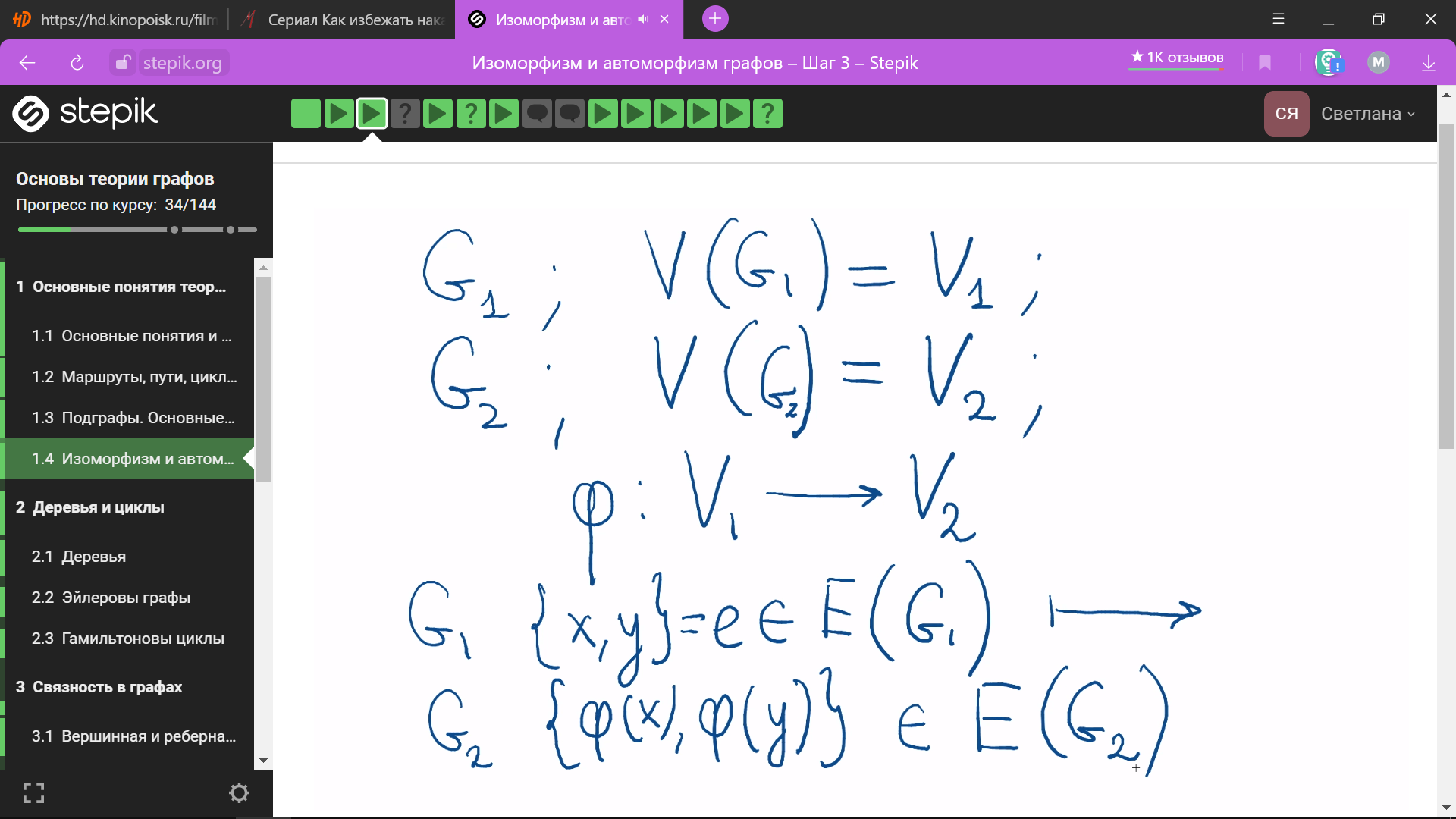
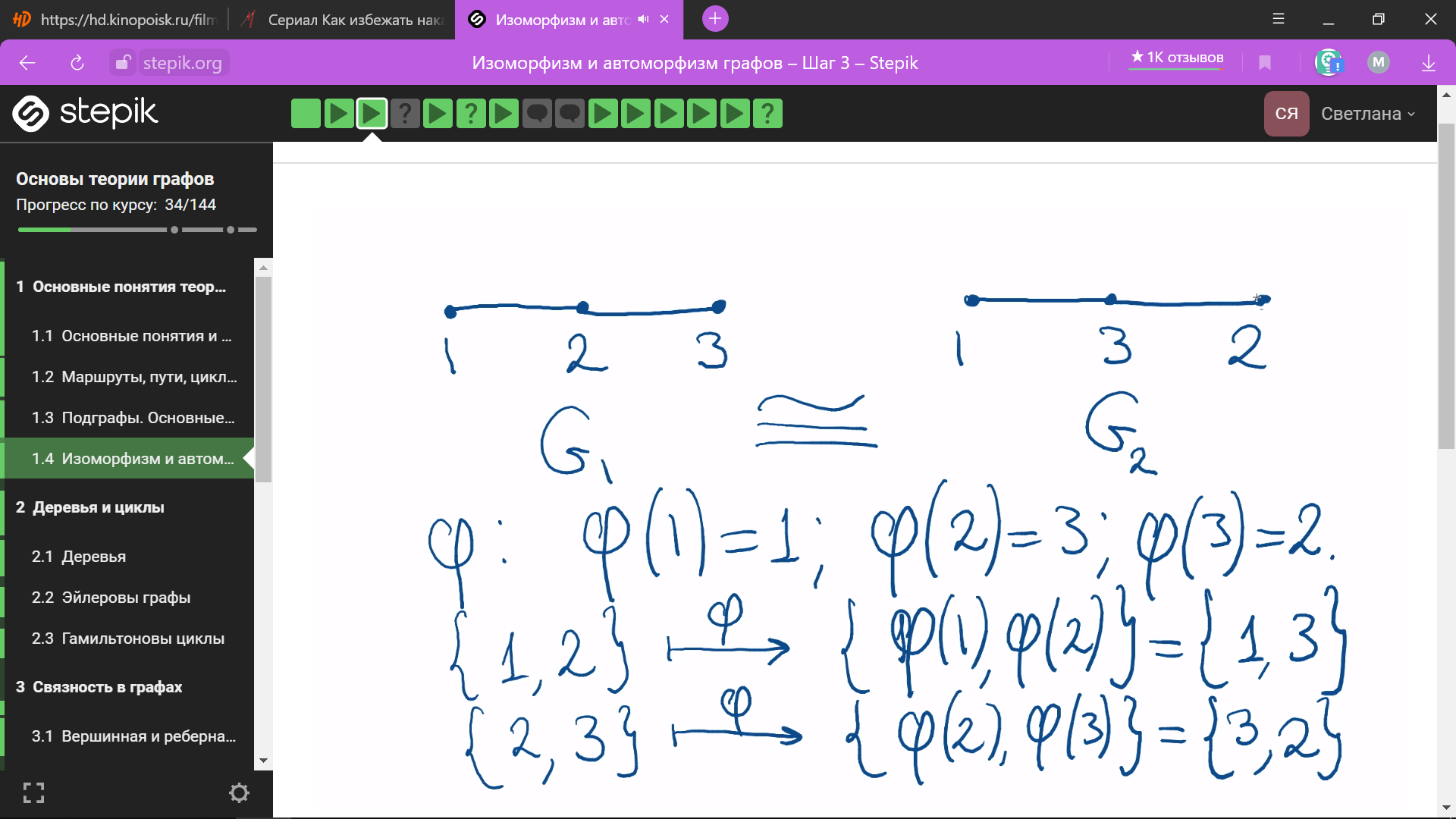 графы
G1
и G2
изоморфны
графы
G1
и G2
изоморфны
Пути, цепи, циклы.
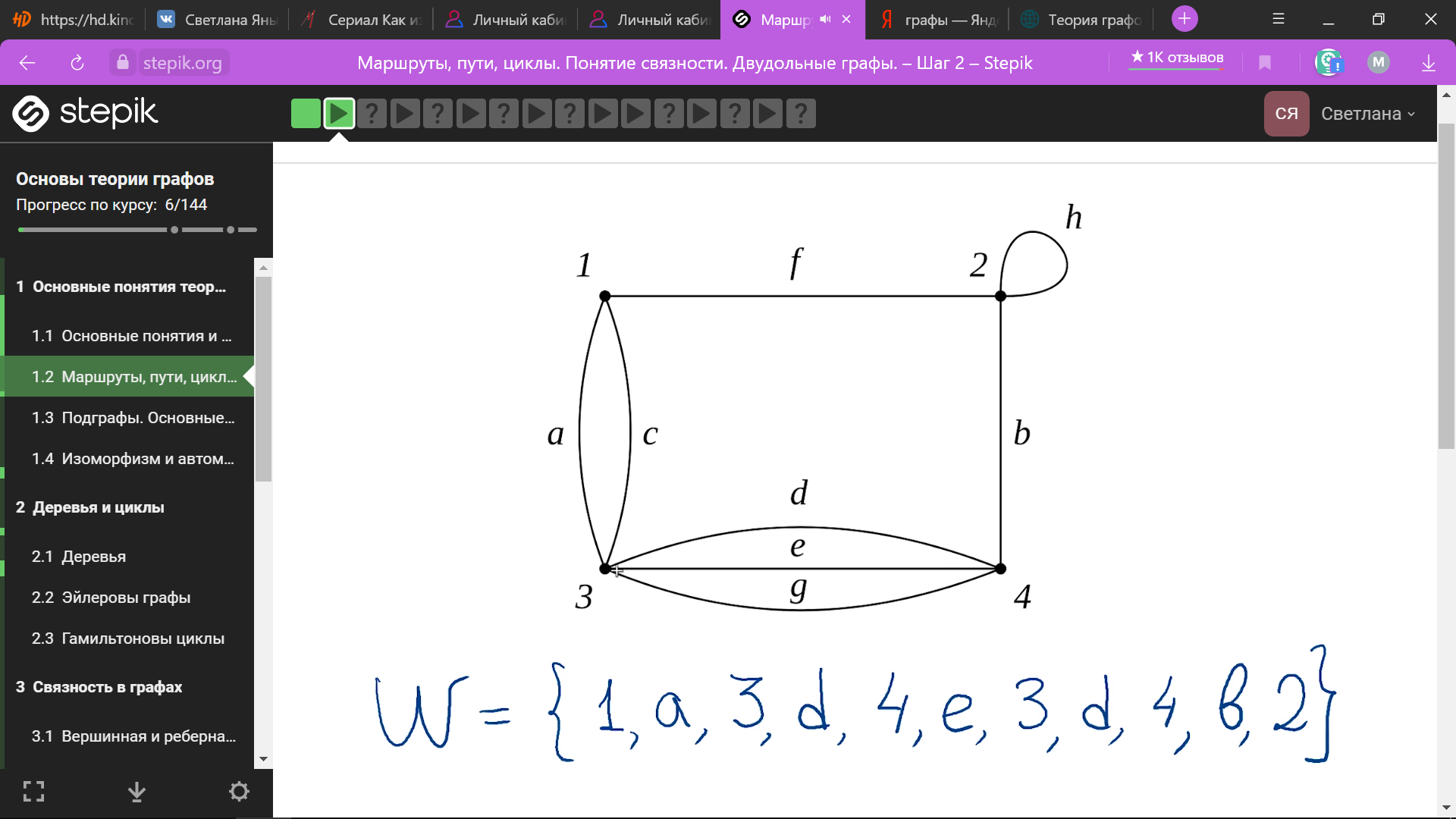 маршрут
маршрут
 путь
(цепь) – рёбра не могут повторяться
путь
(цепь) – рёбра не могут повторяться
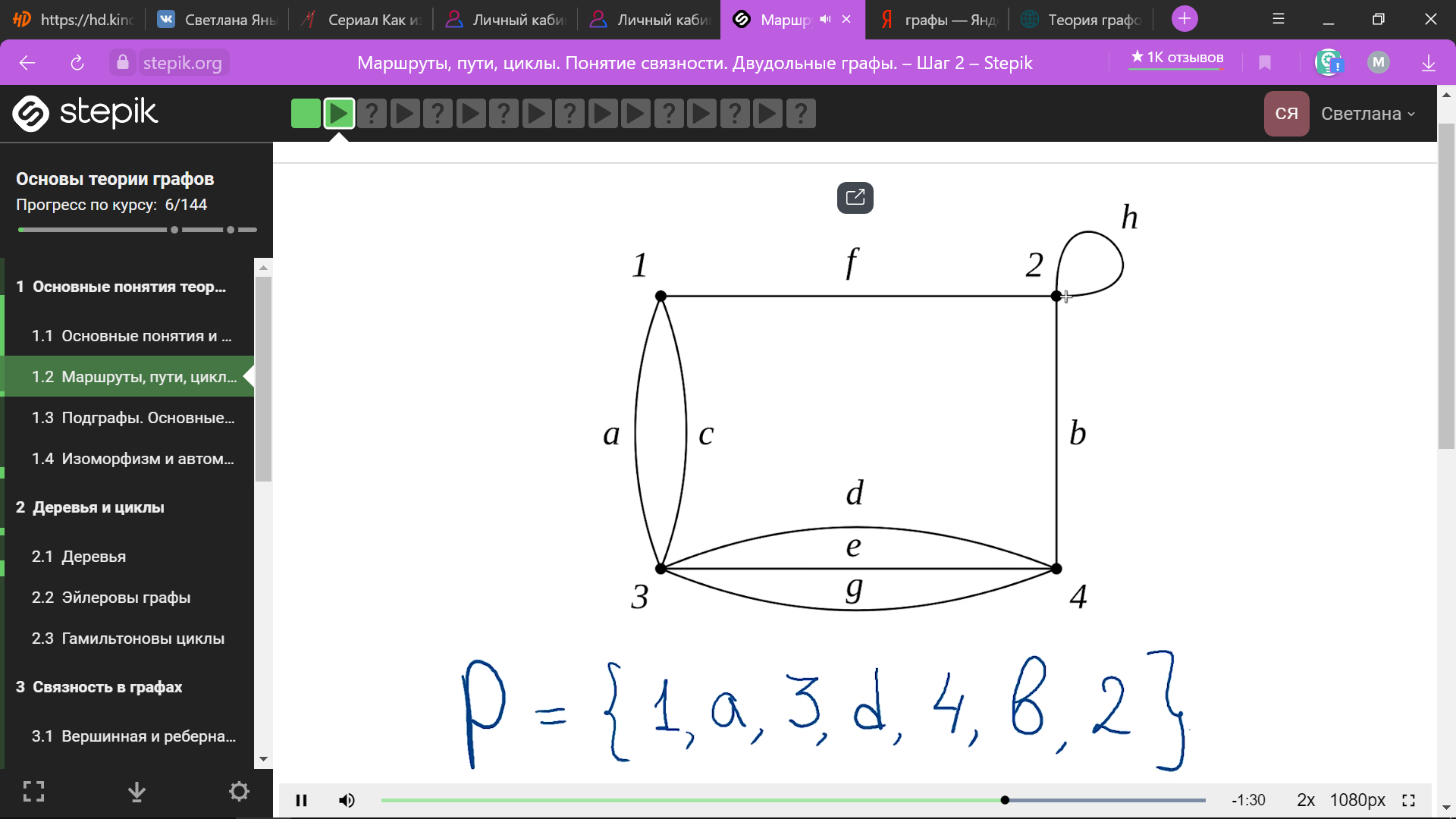 простой
путь – рёбра и вершины не могут повторяться
простой
путь – рёбра и вершины не могут повторяться
Элементарная дуга – это цепь, в которой каждая вершина встречается только один раз
В
простом графе можно описывать путь
только вершинами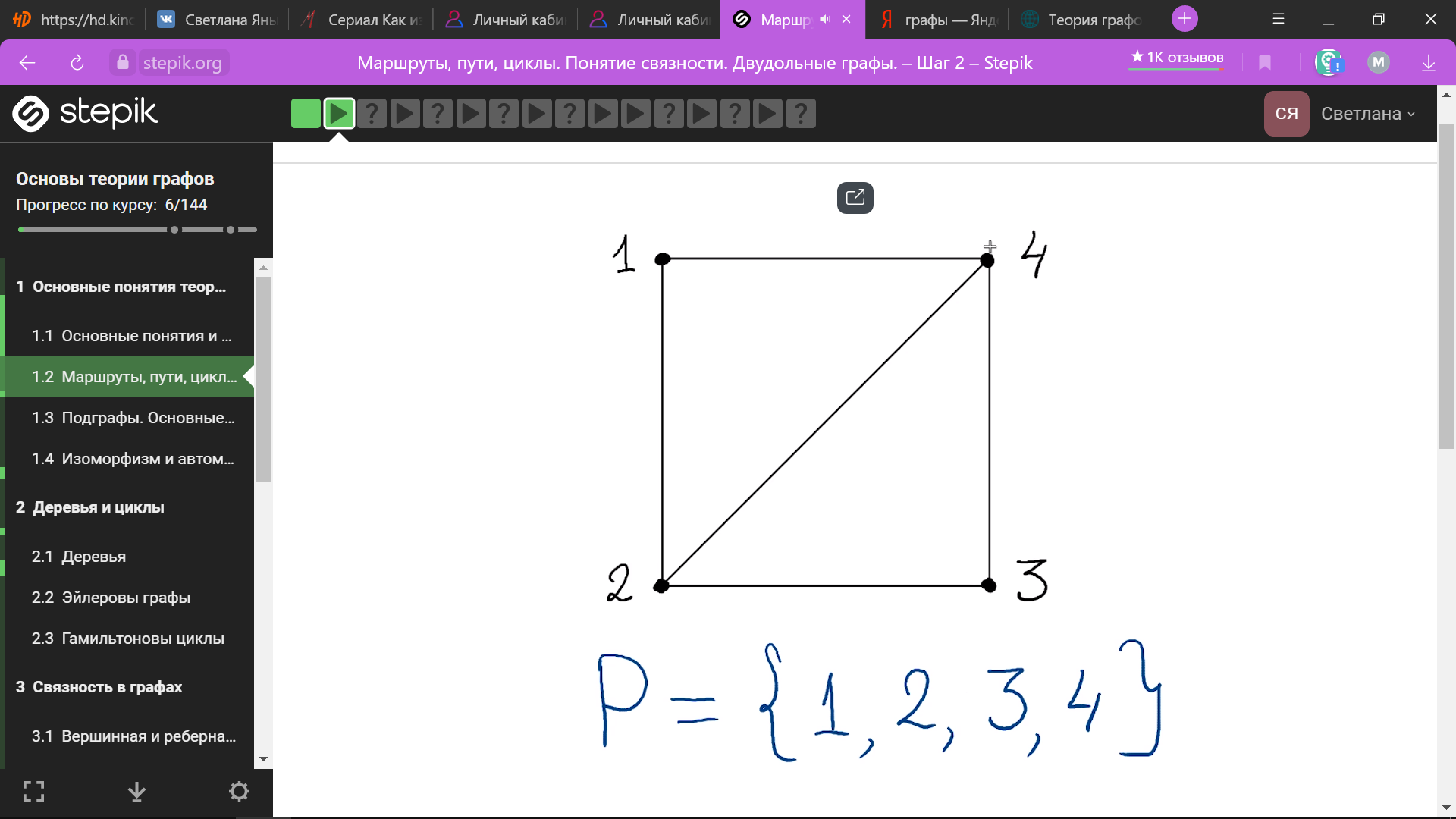
Замкнутый
маршрут – в котором начальные и конечные
вершины совпадают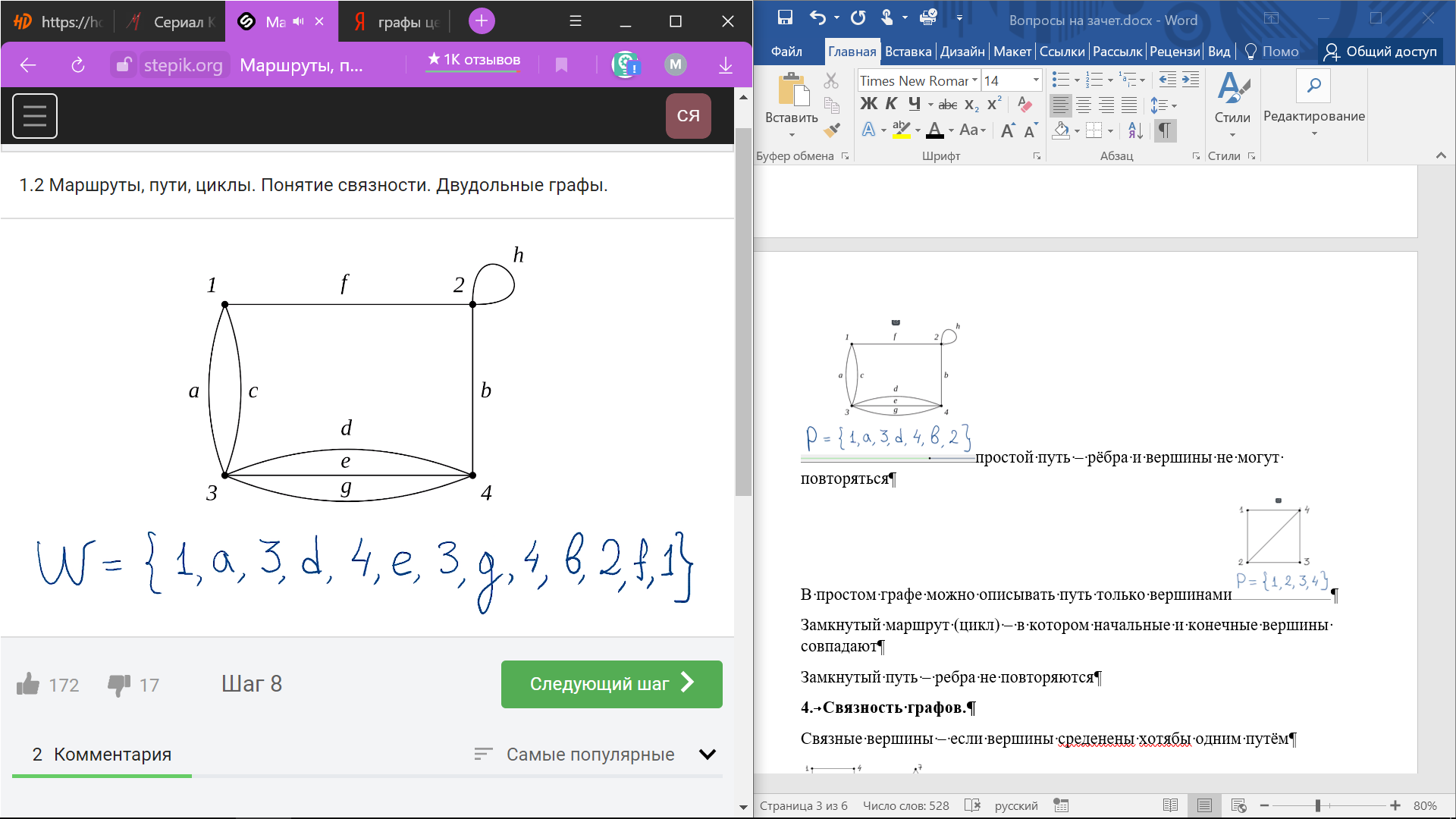
Замкнутый путь – ребра не повторяются
Цикл – маршрут у которого начальные и конечные вершины совпадают и рёбра, и вершины не повторяются.
Обхват – длина минимального цикла, если в графе циклов нет – обхват = бесконечности
Обхват графа больше 3 – граф свободный от треугольников
Изолированная вершина циклом не является
Связность графов.
Связные вершины – если вершины соединены хотя бы одним путём
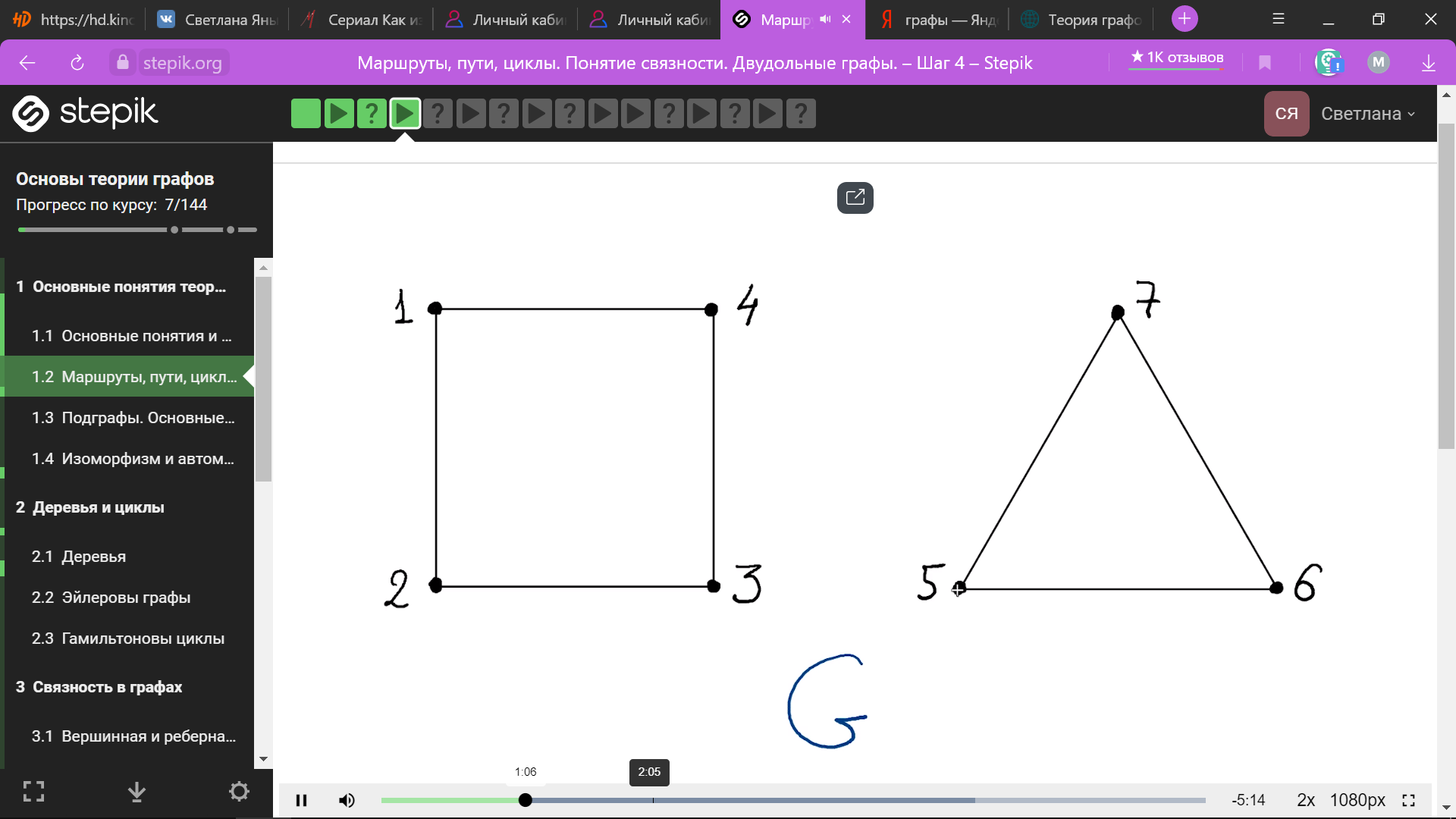 2
и 4 связаны, 1 и 7 не связаны
2
и 4 связаны, 1 и 7 не связаны


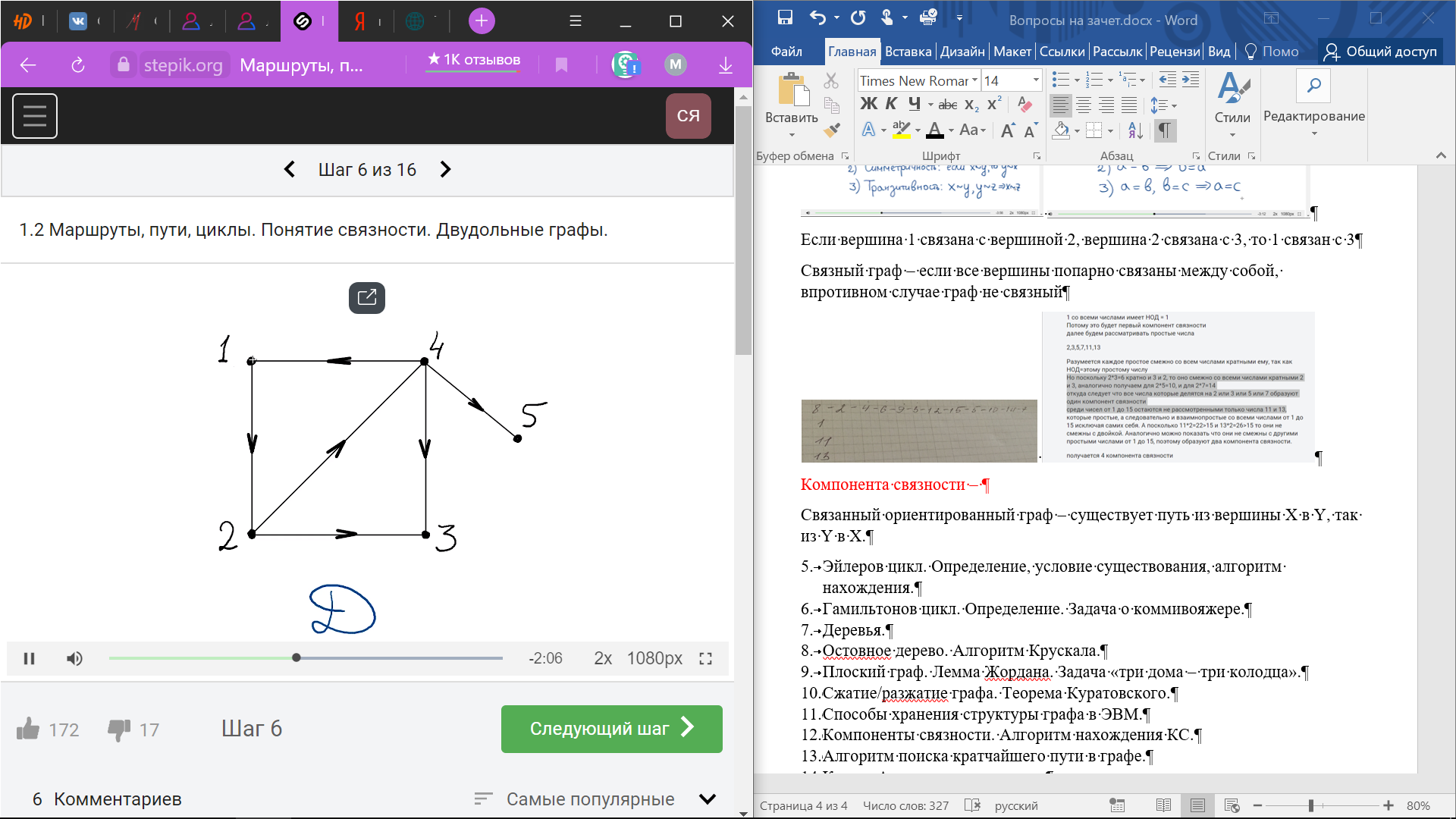
Если вершина 1 связана с вершиной 2, вершина 2 связана с 3, то 1 связан с 3
Связный граф – Это означает, что между любой парой вершин этого графа существует как минимум один путь. если все вершины попарно связаны между собой, впротивном случае граф не связный
Пусть G есть граф, построенный на вершинах 1,2…,15, в котором вершины ii и jj смежны тогда и только тогда, когда их наибольший общий делитель больше единицы. Сколько компонент связности имеет такой граф?

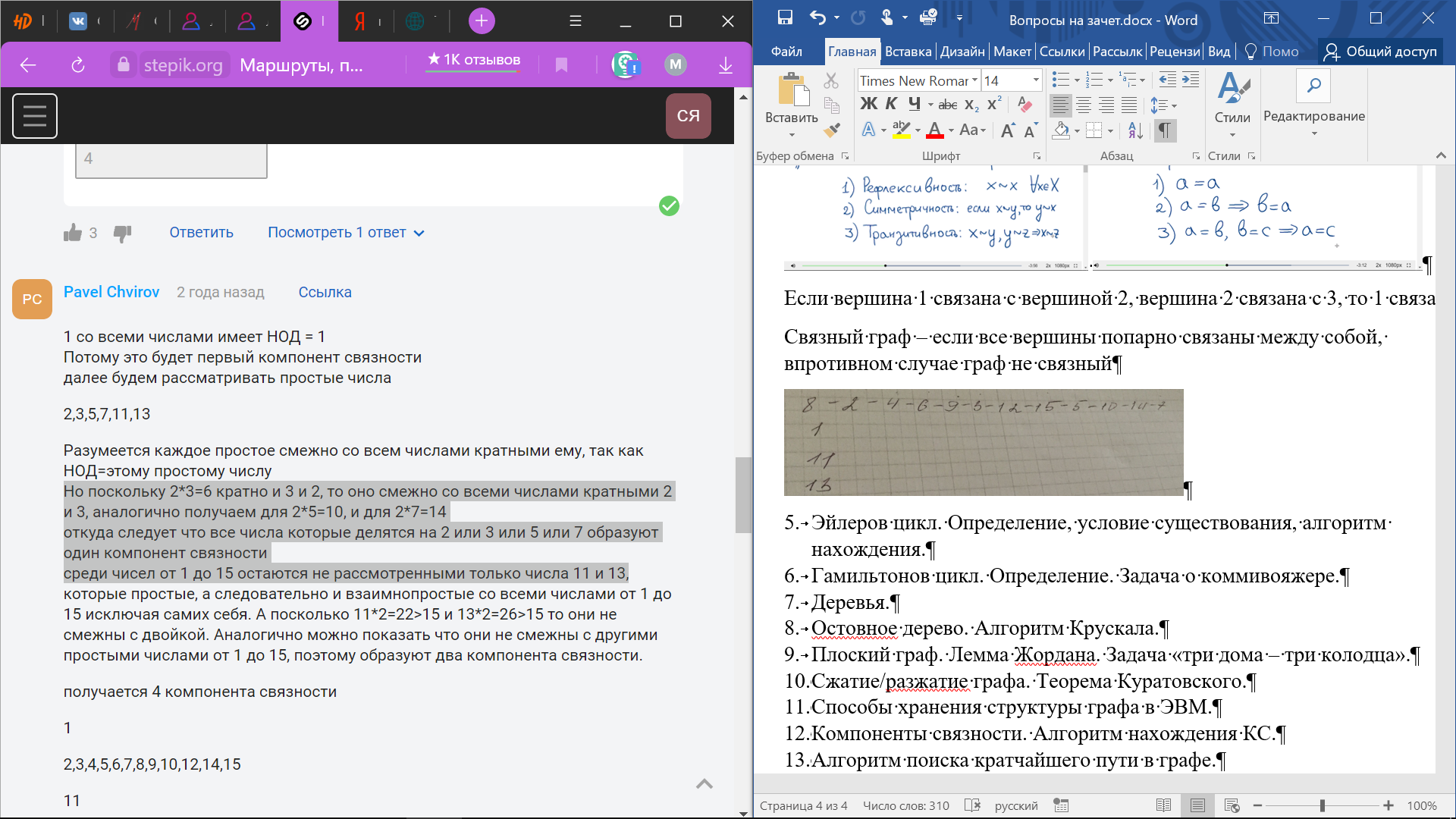
Компонента
связности –
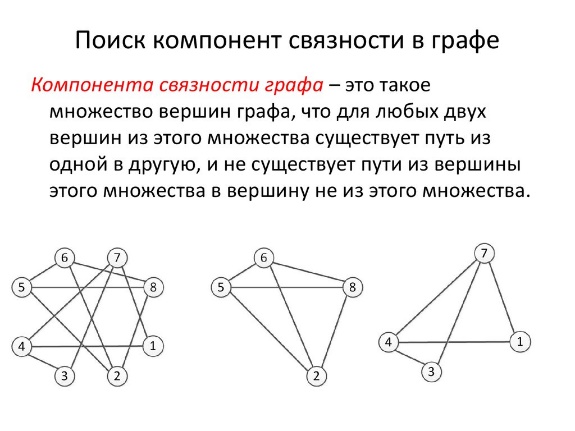
Связанный ориентированный граф – если существует путь из вершины Х в Y, так из Y в Х.
 1
и 4 сазаны между собой путь из 1 в 4 =124
путь из 4 в 1 = 41, вершины 1 и 3 не связаны
1
и 4 сазаны между собой путь из 1 в 4 =124
путь из 4 в 1 = 41, вершины 1 и 3 не связаны
 компоненты
сильной связности
компоненты
сильной связности
Сильно связанный граф – Если граф состоит из единственной такой компоненты
Какое максимальное количество ребер может быть в простом слабо связном ориентированном графе на 10 вершинах, не являющимся сильно связным? Ответ: Каждая вершина из десяти должна соединяться с 9 другими. Но она не может соединяться сама с собой, поэтому мы умножаем 9 не на 10 (по количеству вершин), а так как она соединяется со всеми, кроме себя (простой граф), на девять. 9*9 = 81
Вершинная связность:
Вершинное разделяющие множество (вершинный разрез) – множество вершин после удаление которых граф разваливается на несвязные компоненты.
Вершинная связность – минимальное кол-во вершин которое мы должны удалить в графе для того чтобы граф распался на компоненты связности или чтобы граф стал содержать единственную вершину.

 связность
графов
связность
графов
Вершино
k
связный граф – если граф построен на
![]() вершине и при удалении любых вершин в
количестве меньше k,
граф остаётся связным
вершине и при удалении любых вершин в
количестве меньше k,
граф остаётся связным
Вершинная связность – граф G имеет вершинную связность = k если этот граф является ещё вершино k связным, однако вершино k+1 уже не является
Реберная связность – размер минимального рёберно разделяющего множества для этого графа, тоесть какое минимальное число ребер нужно удалить чтобы граф распался на 2 компоненты связности
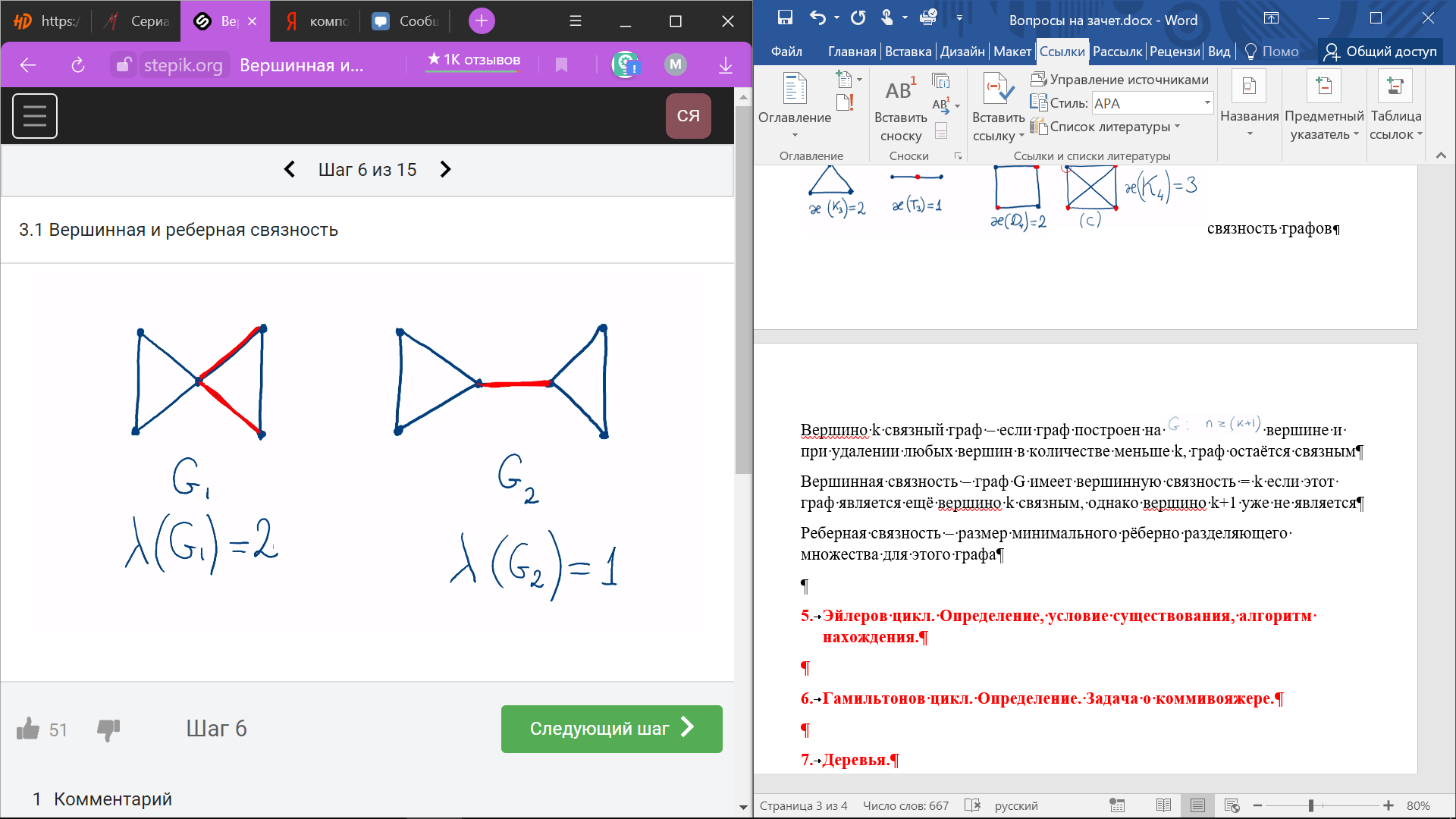 реберная
связность
реберная
связность
Мост – ребро удаление которого приводит к разделению на 2 компоненты связности
Чтобы найти мост нужно поочерёдно удалять одно ребро, до поиска 2ух компонентов связности
Реберно k связный граф – если удаление любых ребер такого графа в количестве меньше чем k не приведёт к потере связности этого графа
Реберная связность графа – максимально возможное значение k, что граф ещё является реберно k связным, но реберно k+1 связным уже не является.
Точкой сочленения называется вершина графа, при удалении которой количество компонент связности возрастает. Для обозначения этого понятия также используются термины «разделяющая вершина» и «шарнир».
Разрез графа – это минимальное количество ребер, которые необходимо удалить, чтобы граф перестал быть связным.
