Исследование операций

Григорьева Наталья Никифоровна

20.02

Целевая функция – линейно зависит от элементов решения, все элементы имеют вид равенств или неравенств

W = W(α,х)

Задача о диете:

	П1	П2	П3
Б	b1	b2	b3	B
Ж	g1	g2	g3	G
У	u1	u2	u3	U
Кл	g1	g2	g3	Q min
	c1	c2	c3	Q max

X = {x₁, x₂, x₃} – элементы решения (количество продукта)

L = c₁x₁+c₂x₂+c₃x₃ → min

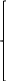
b1x1+b2x2+b3x3≥B

g1x1+g2x2+g3x3≥G

u1x1+u2x2+u3x3≥U

g1x1+g2x2+g3x3≥Qmin

g1x1+g2x2+g3x3≥Qmax

x_i ≥ 0

_______________________________

L = 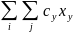→ min

Основная задача линейного программирования (каноническая) ОЗЛП:

Необходимо найти неотрицательные значения Х, которые удовлетворяли бы условиям равенства (фото) и обращали бы в максимум линейную функцию этих переменных.

L_y = c1x1+c2x2+c3x3 → min

L_y = –c1x1–c2x2–c3x3 → max

Фото размазанное переписать

b1x1+b2x2+b3x3–y₁≥B

g1x1+g2x2+g3x3–y₂≥G

u1x1+u2x2+u3x3–y₃≥U

g1x1+g2x2+g3x3–y₄≥Qmin

g1x1+g2x2+g3x3+y₅≥Qmax

{x1,x2,x3,y1,y2,y3,y4,y5}

x_i, y_i ≥ 0

пример у доски =)

Существование решения ОЗЛП и его интерпретация

допустимое, то которое соответствует системе ограничений

оптимальное, то которое обращает функцию в максимум

n – m = 2 = k

m переменных мы можем найти, а остальные 2 являются свободными (k)

свободные {x₁, x₂}

базисные {x₃, x₄, …, x_n}

x₃ = 0

x₂ = -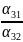 x₁ -

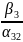
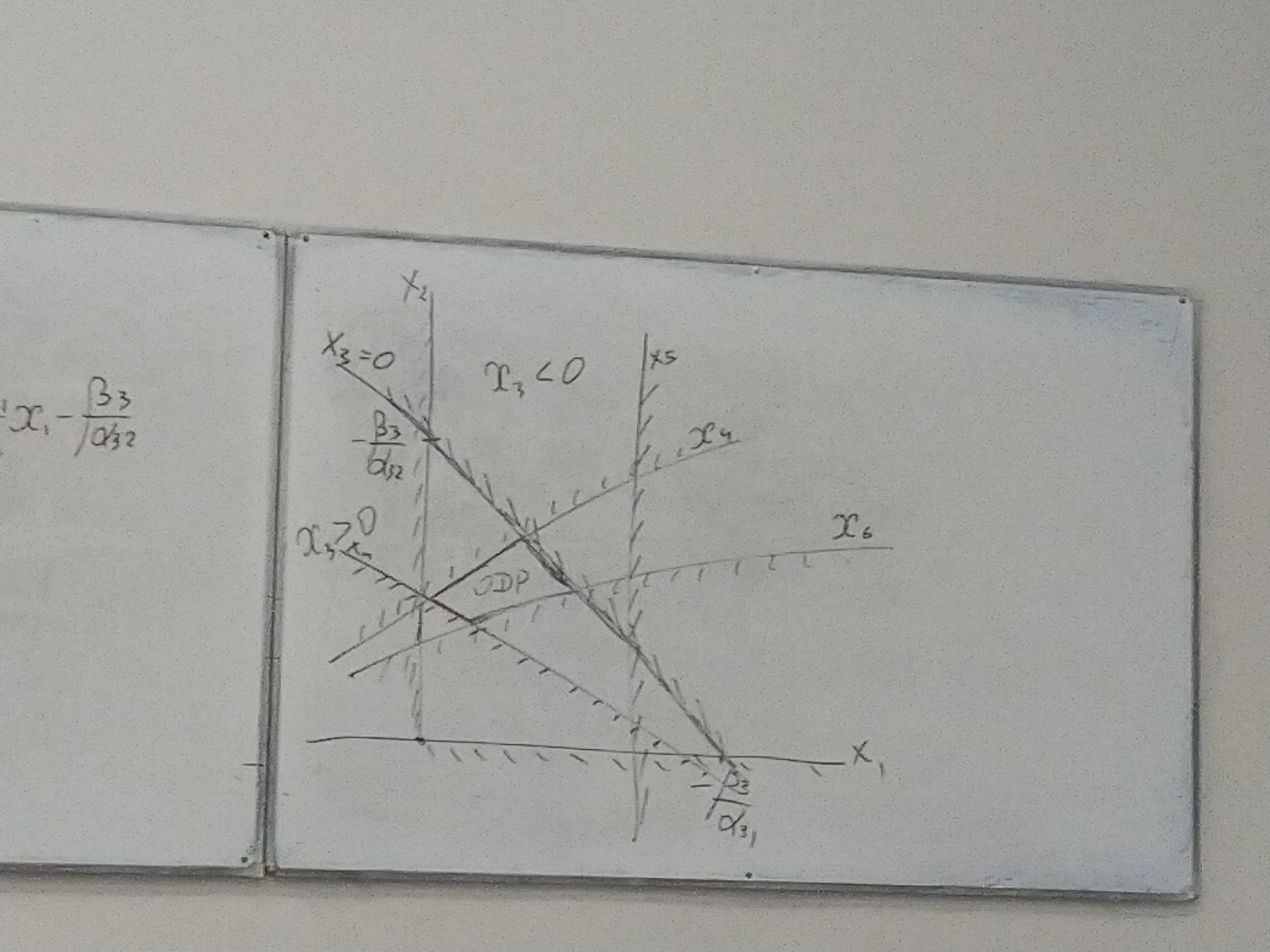
Опорное решение – одна (все) из вершин многогранника.

k элементов решения нулевые!

27.02 Симплекс метод

(в этом случае к min)

k = n – m

X = {x₁,…, x_n} x_i ≥ 0

Алгоритм симплекс метода

1. Выбираются л переменных в качестве свободных и через них выражаются m базисных.

Свободные с {x₁,…x_k}

Базисные {x_k+1,…x_n} m

4. L = γ₁x₁+γ₂x₂+ … +γ_kx_k+γ_n

L₀ = γ₀

пример

5. 

6. I γ < 0 |max|

05.03 Транспортная задача

Имеется М пунктов отправления и N пунктов прибытия. Груз измеряется в штуках.

A₁…A_n, a₁…a_n

B₁…B_n, b₁…b_n

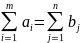
	c11	c12	…	c1n
	c21	c22		c2n
	:
	сm1	cm2	…	cmn

C

1 шт a_i→b_j

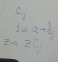
План перевозок

L = 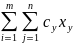→ min

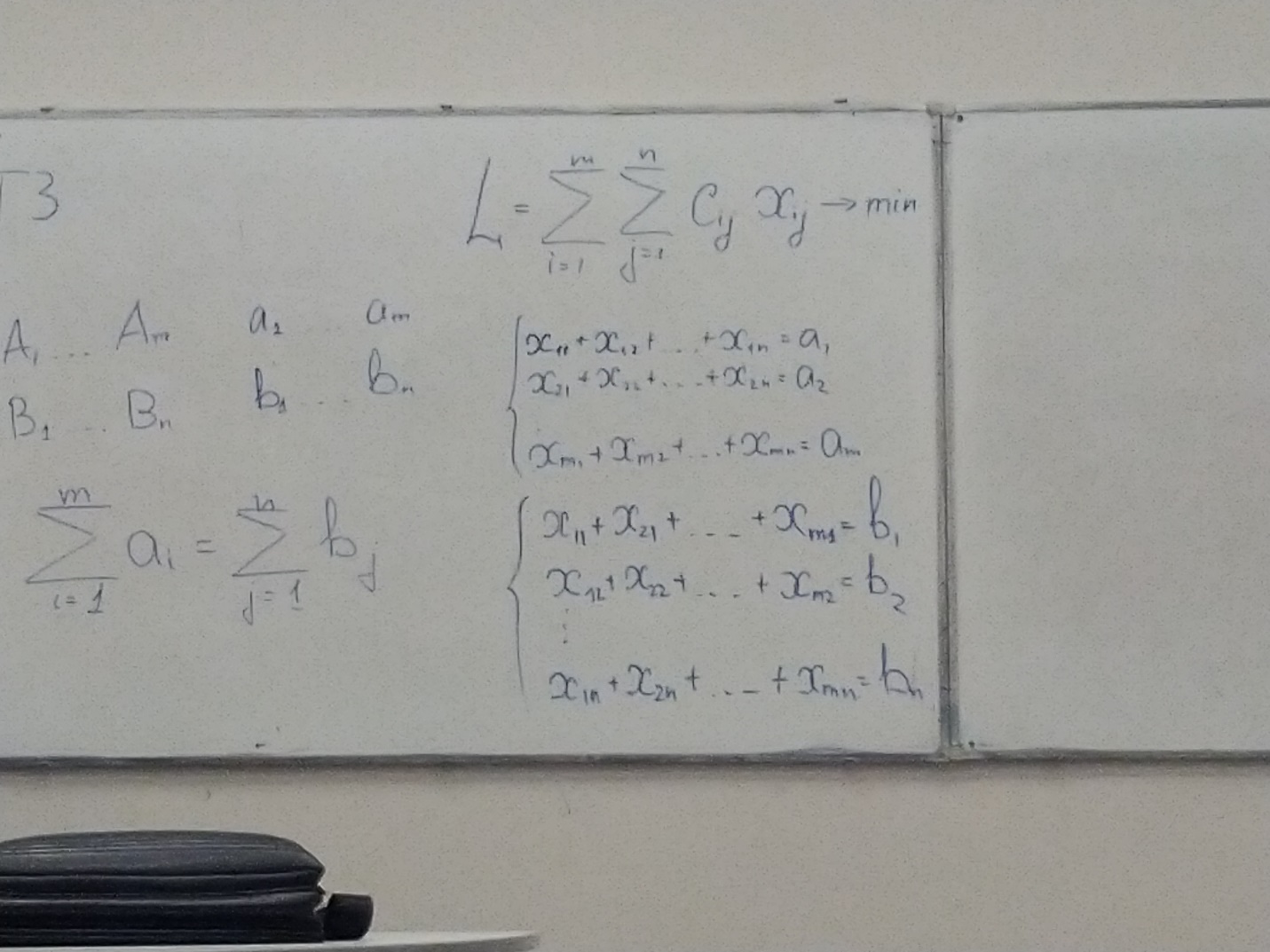
m*n – всего решений

m+n-1

k=mn-m-n+1 = (n-1)(m-1)

Методы составления опорного плана транспортной задачи

	B1	B2	B3	B4	ai запасы
A1	(перевозка единицы товара) 7	6	3	5	30
A2	6	5	4	5	118
A3	3	5	3	4	52
bj заявки	25	44	81	50	200

m= 3 12

n=4

(m-1)(n-1)=6 k=6

Метод северо-западного угла

	B1	B2	B3	B4	ai запасы
A1	7 25	6 5	3	5	30-25=5
A2	6	5 39	4 79	5	118-39=79
A3	3	5	3 2	4 50	52-2=50
bj заявки	25	44	81	50	200

L_{северо-запад} = (25*7)+30+195+316+6+200 = 922

Минимальная стоимость (минимального элемента)

Каждый раз ищем минимальный элемент в столбце

	B1	B2	B3	B4	ai запасы
A1	7	6	(минимальный элемент)3 30	5	30
A2	6	5 44	4 24	5 50	118-24=94
A3	3 25	5	3 27	4	52-25=27
bj заявки	25	44	81-30=51 51-27=24	50	200

L = 90+220+96++250+(25*3)+81 = 812

Метод (алгоритм) двойного предпочтения

Выбираем минимальную стоимость в столбце и в строке, ставим максимум где 2 плюса, далее заполняем где 1 плюс.

	B1	B2	B3	B4	ai запасы
A1	7	6	++ 3 30	5	30
A2	6	+ 5 44	+ 4 51	5 23	118
A3	++ 3 25	5	3	+ 4 27	52
bj заявки	25	44	81	50	200

L = 90+220+204+115+75+108 = 812

Метод Фогеля

Выбираем клетку с минимальной стоимостью у максимальной дельты (25, 30 …). После 1 подсчёта пересчитываем дельту.

	B1	B2	B3	B4	ai запасы	∆ между двумя минимальными стоимостями
A1	7	6	3 30	5	30	(5-3=)2, 2
A2	6	5 44	4 51	5 23	118	1, 1, 0
A3	3 25	5	3	4 27	52	1, 1, 1
bj заявки	25	44	81	50	200
∆ между двумя минимальными стоимостями	3	1, 0	1, 1	1, 1

L = 812

Сделать пример самой 3мя способами

Двойное предпочтение

	B1	B2	B3	ai запасы
A1	++ 3 15	7	+ 4 25	40
A2	8	+ 3 40	6 40	80
A3	5	++ 2 30	8	30
bj заявки	15	70	65

L = 45+100+120+240+60 = 565

П оиск циклов с отрицательной ценой . Цикл, перетаскиваем по кругу единицы товара

-8+6-3+2 = -3

-8+4-3+5 = -2

Метод потенциалов

Считаем альфа и бета, задаём альфа 1 и находим всё остальное, заполняем пустые клетки (сложение найденных альфа и бета). Если больше, это хорошая клетка, там, где больше потенциал ищем для этой клетки цикл. Повторяем до тех пор, пока не найдём минимум.

12.03 Теория двойственность

W = → max

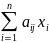≤ b_j

j =

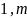
y_j – двойственная модель

W_{двойственная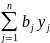} = → min

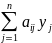≥ c_i

Исходная задача, двойственная задача

двойственные оценки

Правила составления двойственной задачи:

1. формальная – целевая функция максимизируется, то двойственная минимизируется, ограничения стоят со знаком меньше или равно, то в двойственной больше или равно

2. матрица коэффициентов целевой и матрица двойственной задачи связаны транспонированием

3. число переменных в двойственной задаче равно числу ограничений в исходной, число ограничений в двойственной равно числу переменных в исходной

4. Коэффициенты при неизвестных – свободные члены в исходной задаче

каждому ограничению одной из задач соответствует переменная другой задачи

если в исходной задаче ограничение - равенство, то в двойственной задаче переменные могут иметь любое значение

Первая теорема двойственности

Для взаимодвойственных задач линейного программирования имеет место один из взаимоисключающих случаев

1. В исходной и двойственной имеются оптимальные решения, при этом значения целевых функций совпадают

2. В исходной задаче допустимо множество не пусто, но целевая функция с верху не ограничена, у двойственной будет пустая область допустимых значений

3. В двойственной задаче не пустая область допустимых решений целевая функция не ограничена снизу

4. Нулевые одр (пустые)

Вторая теорема двойственности (о дополняющей не жёсткости)

Для того чтобы они были оптимальными решениями необходимо и достаточно чтобы выполнялись соотношения:

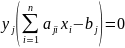
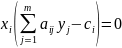
Третья теорема двойственности (об оценках)

Значения y_j в оптимальном решении двойственной задачи представляют собой оценку влияния свободных членов b_j исходной задачи на величину целевой функции исходной задачи.

∆W_{исходное} = ∆b_jy_j

	П1	П2	П3	П4	запасы Mi
M1	4	2	2	3	35
M2	1	1	2	3	30
M3	3	1	2	1	40
	14	10	14	11

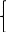X = {x₁, x₂, x₃, x₄}

4x₁+2x₂+2x₃+3x₄ ≤ 35

x₁+x₂+2x₃+3x₄ ≤ 30

3x₁+x₂+2x₃+x₄ ≤ 40

14x₁+10x₂+14x₃+11x₄ → max

Y = {y₁, y₂, y₃}

4y₁+y₂+3y₃ ≤ 14

2y₁+y₂+y₃ ≤ 10

2y₁+2y₂+2y₃ ≤ 14

3y₁+3y₂+y₃ ≤ 11

35y₁+30y₂+40y₃ → min

X = {0; 5; 12,5; 0}

Y = {3; 4; 0}

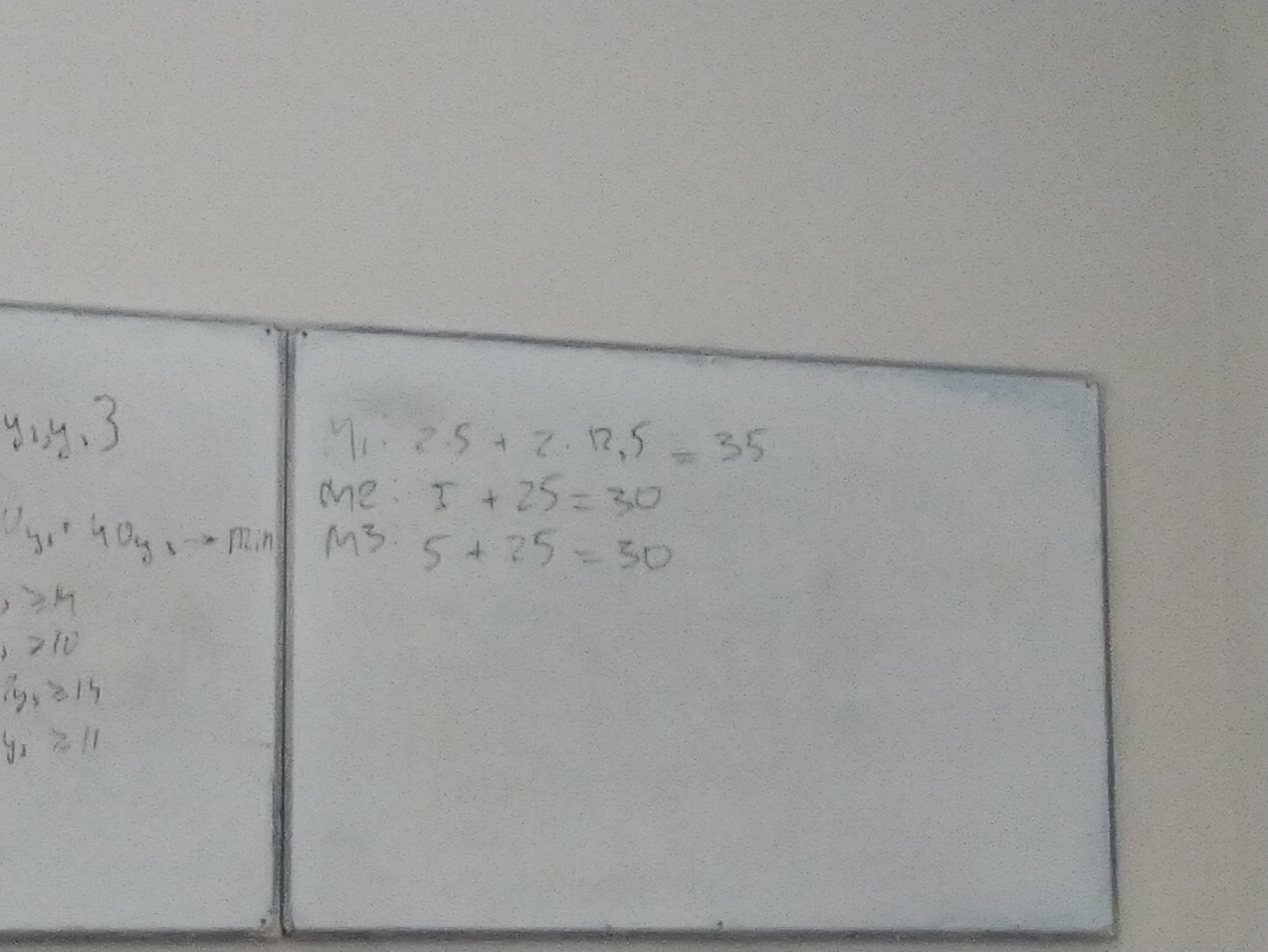
План производства и набор оценок оптимальны тогда и только тогда, когда прибыль от реализации определённая при известных ценах продукции равна затратам на ресурсы по внутренним ценам, для всех других планов прибыль не превышает стоимости затраченных ресурсов, следовательно, ценность выпускаемых ресурсов ниже ценности суммарной продукции

Если оценка ресурса Y больше нуля, то при оптимальной производственной программе этот ресурс используется полностью, иначе Y = 0

Если какой-то вид продукции вошёл в оптимальный план, то он в оптимальных оценках не убыточен

19.03 Задача целочисленного программирования