5. Метод Крамера

А =

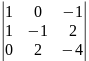
B = (1,1,1)

Определим оптимальную стратегию x = (x₁, x₂, x₃) игрока А и цену игры ν.

∆а = = 1·(-1)·(-4) + 1·2·(-1) – 1·2·2 = -2

Заменим 1-й столбец транспонированной матрицы А на вектор В. Найдем определитель полученной матрицы.

∆а₁ = 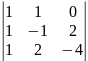= 1·(-1)·(-4) + 1·2·1 – 1·2·2 - 1·1·(-4) = 6

Заменим 2-й столбец транспонированной матрицы А на вектор результата В. Найдем определитель полученной матрицы.

∆а₂ = = 1·1·(-4) + 1·2·(-1) – 1·2·1 = -8

Заменим 3-й столбец транспонированной матрицы А на вектор результата В. Найдем определитель полученной матрицы.

∆a₃ = 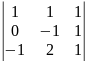= 1·(-1)·1 + 1·1·(-1) – 1·(-1)·(-1) – 1·1·2 = -5

Следовательно:

ν = = =

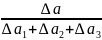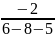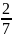
x₁ = = =

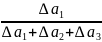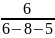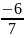
x₂ = = =

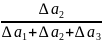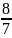
x₃ = = =

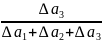Определим оптимальную стратегию y = (y₁, y₂, y₃) игрока B.

Заменим 1-й столбец матрицы А на вектор В. Найдем определитель полученной матрицы.

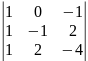∆ã₁ = = 1·(-1)·(-4) + (-1)·1·2 – (-1)·(-1)·1 – 1·2·2 = -3

Заменим 2-й столбец матрицы А на вектор результата В. Найдем определитель полученной матрицы.

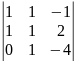∆ã₂ = = 1·1·(-4) + (-1)·1·1 – 1·2·1 – 1·1·(-4) = -3

Заменим 3-й столбец матрицы А на вектор результата В. Найдем определитель полученной матрицы.

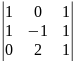∆ã₃ = = 1·(-1)·1 + 1·1·2 – 1·1·2 = -1

Следовательно:

y₁ = = =

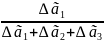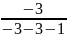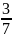
y₂ = = =

y₃ = = =

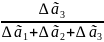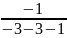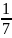
Ответ: Оптимальная стратегия игрока А x = (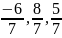 ), оптимальная стратегия игрока В y = (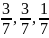 ), цена игры -2.

2. Биматричные игры

C = a₁₁ – a₁₂ – a₂₁ + a₂₂

α = a₂₂ – a₁₂

D = b₁₁ – b₁₂ – b₂₁ + b₂₂

β = b₂₂ – b₂₁

C = 6 – 2 – 2 + 4 = 6

α = 4 – 2 = 2

D = 2 – 6 – 8 + 2 = -10

β = 2 – 8 = -6

(p–1)(6q-2) ≥ 0

p(6q-2) ≥ 0

(q-1)(-10p+6) ≥ 0

q(-10p+6) ≥ 0

получаем:

1) p = 1,q ≥

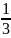
p = 0, q ≤

0 ≤ p ≤ 1, q =

2) q = 1,p ≤

q = 0, p ≥

0 ≤ q ≤ 1, p =

Игра имеет единственную ситуацию равновесия (P*,Q*), где оптимальными стратегиями являются: P* = ( ; 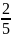); Q* = ( ; ).

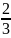Рисунок 8 - График

Игрок 1 должен использовать стратегии 1 и 2 с частотами и , а игрок 2 –стратегии 1 и 2 с частотами и .

Цена игры для первого игрока:

H_a( ; ) =

Цена игры для второго игрока:

H_b( ; ) =

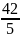
Ответ: P* = ( ; ); Q* = ( ; ). Выигрыш игроков в равновесной ситуации: f(P*,Q*) = ( ; ).

ВЫВОД

Был получен навык решения стратегических задач, различными методами.