22)Определение собственного числа и собственного вектора квадратной матрицы

Собственным вектором квадратной матрицы M называется вектор , который удовлетворяет соотношению , где — собственное значение, соответствующее данному собственному вектору. Одному собственному значению может соответствовать несколько (линейно независимых) собственных векторов, в таком случае говорят о собственном подпространстве для данного собственного значения. Собственными векторами линейного преобразования называются собственные вектора матрицы, определяющей это преобразование.

Свойства собственных векторов и значений  Линейная комбинация собственных векторов матрицы , соответствующих одному и тому же собственному значению , также является собственным вектором с собственным значением .

1Количество различных собственных значений не может превышать размер матрицы.

2Сумма размерностей собственных подпространств, соответствующих всем собственным значениям равна размерности матрицы (в случае рассмотрения комплексных чисел).

3Собственные векторы, самосопряженного оператора А соответствующие различным собственным значениям ортогональны.

Т. е. если , и , то 

Для произвольной матрицы это не верно.

24) подобные матрицы их собственные числа

Квадратные матрицы A и B одинакового порядка называются подобными, если существует невырожденная матрица P того же порядка, такая что:

Подобные матрицы получаются при задании матрицей линейного преобразования в разных координатных системах; при этом матрица Р является матрицей перехода от одной системы к другой. Свойства

Отношение подобности матриц является отношением эквивалентности в пространстве квадратных матриц.

У подобных матриц совпадают многие характеристики, а именно:

• ранг

• определитель

• след

• собственные значения (но собственные векторы могут не совпадать)

• характеристический многочлен

• Жорданова форма с точностью до перестановки клеток

Можно доказать, что любая матрица A подобна A^T.

 Собственными числами матрицы являются корни уравнения

и только они.

        Доказательство.     Пусть столбец -- собственный вектор матрицы с собственным числом . Тогда, по определению, . Это равенство можно переписать в виде . Так как для единичной матрицы выполнено , то . По свойству матричного умножения и предыдущее равенство принимает вид

(19.4)

Допустим, что определитель матрицы отличен от нуля, . Тогда у этой матрицы существует обратная 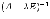. Из равенства (19.4) получим, что , что противоречит определению собственного вектора. Значит, предположение, что , неверно, то есть все собственные числа должны являться корнями уравнения .

Пусть -- корень уравнения . Тогда базисный минор матрицы не может совпадать с определителем матрицы и поэтому , -- порядок матрицы . Уравнение (19.4) является матричной записью однородной системы линейных уравнений с неизвестными , являющимися элементами матрицы-столбца . По  теореме 15.3 число решений в фундаментальной системе решений равно , что больше нуля. Таким образом, система (19.4) имеет хотя бы одно ненулевое решение, то есть числу соответствует хотя бы один собственный вектор матрицы .      

Определитель является многочленом степени от переменного , так как при вычислении определителя никаких арифметических действий кроме сложения, вычитания и умножения выполнять не приходится.

26) Квадратичной формой называется функция B(x) = A(x,x) из линейного пространства L над произвольным полем F характеристики не 2 в поле F, которая получается избилинейной формы A(x,y) при x = y.

При фиксированном базисе в L квадратичная форма имеет вид

где , а a_ij = a_ji.

Матрицу (a_ij) называют матрицей квадратичной формы в данном базисе.