Обратная матрица

Определим операцию деления матриц как операцию, обратную умножению.

 

            Определение. Если существуют квадратные матрицы Х и А одного порядка, удовлетворяющие условию:

XA = AX = E,

где Е - единичная матрица того же самого порядка, что и матрица А, то матрица Х называется обратной к матрице А и обозначается А^-1.

 Каждая квадратная матрица с определителем, не равным нулю имеет обратную матрицу и притом только Рассмотрим общий подход к нахождению обратной матрицы.

Исходя из определения произведения матриц, можно записать:

AX = E  , i=(1,n), j=(1,n),

e_ij = 0,                      i  j,

e_ij = 1,                       i = j .

Таким образом, получаем систему уравнений:

,

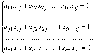Решив эту систему, находим элементы матрицы Х.

Однако, такой способ не удобен при нахождении обратных матриц больших порядков, поэтому обычно применяют следующую формулу:

где М_ji- дополнительный минор элемента а_ji матрицы А.

Cвойства обратных матриц

кажем следующие свойства обратных матриц:

1. (A^-1)^-1 = A;

2. (AB)^-1 = B^-1A^-1

3. (A^T)^-1 = (A^-1)^T.

10) Линейная зависимость

Линейная зависимость (матем.), соотношение вида

C₁₁u₁ + C₂u₂ + ... + C_nu_n = 0, (*)

где С₁, C₂, ..., C_n — числа, из которых хотя бы одно отлично от нуля, а u₁, u₂, ..., u_n — те или иные матем. объекты, для которых определены операции сложения и умножения на число. В соотношение (*) объекты u₁, u₂, ..., u_n входят в 1-й степени, т. е. линейно; поэтому описываемая этим соотношением зависимость между ними называется линейной. Знак равенства в формуле (*) может иметь различный смысл и в каждом конкретном случае должен быть разъяснён. Понятие Л. з. употребляется во многих разделах математики. Так, можно говорить о Л. з. между векторами, между функциями от одного или нескольких переменных, между элементами линейного пространства и т. д. Если между объектами u₁, u₂, ..., u_n имеется Л. з., то говорят, что эти объекты линейно зависимы; в противном случае их называется линейно независимыми. Если объекты u₁, u₂, ..., u_n линейно зависимы, то хотя бы один из них является линейной комбинацией остальных, т. е.

u₁ = a ₁u₁ + ... + a _i-1u_i-1 + a _i+1u_i+1 + ... + a _nu_n.

Непрерывные функции от одного переменного

u₁ = j ₁(х), u₂ = j ₂(х), ..., u_n = j _n(x) называются линейно зависимыми, если между ними имеется соотношение вида (*), в котором знак равенства понимается как тождество относительно х. Для того чтобы функции j ₁(x), j₂(x), ..., j _n(x), заданные на некотором отрезке а £ х £ b, были линейно зависимы, необходимо и достаточно, чтобы обращался в нуль их определитель Грама

где

i, k = 1,2, ..., n.

Если же функции j₁ (x), j₂(x), ..., j_n(x) являются решениями линейного дифференциального уравнения, то для существования Л. з. между ними необходимо и достаточно, чтобы вронскиан обращался в нуль хотя бы в одной точке.

Линейные формы от m переменных

u₁ = a_i1x₁ + a_i2x₂ + ... + a_imx_m

(i = 1, 2, ..., n)

называются линейно зависимыми, если существует соотношение вида (*), в котором знак равенства понимается как тождество относительно всех переменных x₁, x₂, ..., x_m. Для того чтобы n линейных форм от n переменных были линейно зависимы, необходимо и достаточно, чтобы обращался в нуль определитель

D=   

Свойство 1. Если среди векторов есть нулевой вектор, то эти векторы линейно зависимы.

            Свойство 2. Если к системе линейно зависимых векторов добавить один или несколько векторов, то полученная система тоже будет линейно зависима.

            Свойство 3. Система векторов линейно зависима тогда и только тогда, когда один из векторов раскладывается в линейную комбинацию остальных векторов.

            Свойство 4. Любые 2 коллинеарных вектора линейно зависимы и, наоборот, любые 2 линейно зависимые векторы коллинеарны.

            Свойство 5. Любые 3 компланарных вектора линейно зависимы и, наоборот, любые 3 линейно зависимые векторы компланарны.

            Свойство 6. Любые 4 вектора линейно зависимы.

Пусть V будет линейное пространство над полем K и . M называется линейно независимым множеством, если любое его конечное подмножество является линейно независимым.

Конечное множество M' = {v₁,v₂,...,v_n} называется линейно независимым, если единственная линейная комбинация, равная нулю, тривиальна, то есть состоит из факторов, равных нулю:

Если существует такая линейная комбинация с минимум одним , M' называется линейно зависимым. Обратите внимание, что в первом равенстве подразумевается , а во втором .