5.2 задача

Задача 4.2. Построение и анализ уравнения множественной линейной регрессии.

Условие. В предшествующей работе выявлен оптимальный состав переменных для построения корректной модели множественной регрессии. Исходные данные представлены в приложении 1.

Требуется, используя средства MS EXCEL:

1. построить множественную модель с использованием встроенного инструмента «Регрессия»;

2. оценить показатели тесноты связи;

3. дать оценку значимости (достоверности) уравнения в целом и параметрам, провести интерпретацию коэффициентов чистой регрессии;

4. рассчитать и проанализировать стандартизованные коэффициенты регрессии и коэффициенты раздельной детерминации;

5. рассчитать и оценить прогнозное значение стоимости квартиры при заданных значениях факторов.

Решение.

1. Построим модель с использованием инструмента «Регрессия», в итоге получим выходные данные (табл. 4.2.1).

Табл. 4.2.1 – а ВЫВОД ИТОГОВ
Регрессионная статистика
R множественный		0,946
R-квадрат		0,896
Нормир. R-квадрат		0,888
Стандарт. ошибка.		297,214
Наблюдения		30
Дисперсионный анализ
	df			SS		MS		F		Значимость F
Регрессия	2			20452522,54		10226261,27		115,76		5,68217E-14
Остаток	27			2385082,74		88336,40
Итого	29			22837605,28
	Коэфф.			Станд. Ош.		t-стат.		P-Значение		Нижние 95%		Верхние 95%
Y-пересечение	-1025,883			175,421		-5,85		0,0000		-1385,82		-665,9475268
X1	56,228			15,862		3,54		0,0015		23,68		88,7748150
X3	20,484			2,058		9,96		0,0000		16,26		24,7061147

Все коэффициенты чистой регрессии имеют Р-значения меньше принятого уровня значимости (0,05), следовательно, признаются достоверными. Выборочная модель множественной линейной регрессии может быть записана в виде:

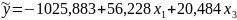
2. Оценим показатели тесноты связи.

EXCEL автоматически рассчитал коэффициенты множественной корреляции (множественный R) и детерминации (R-квадрат), а также скорректированный коэффициент детерминации (нормированный R-квадрат) (табл. 4.2.1).

Напомним, что коэффициент множественной детерминации определяется по формуле: , где W – общий, – воспроизведенный уравнением, а W_е – остаточный объем вариации.

Множественный коэффициент корреляции (R) и скорректированный коэффициент детерминации: ( )_{: ,}

где n – число наблюдений (n=30), p – число регрессоров (факторов) в уравнении, в нашем случае p=2).

чувствителен к увеличению числа регрессоров и уменьшению числа наблюдений, чем больше факторов включено в модель и чем меньше число наблюдений, тем больше различия между множественным коэффициентом детерминации и скорректированной его величиной.

Мы получили следующие показатели тесноты связи: R²=0,896, , R=0,946. Между коэффициентом детерминации и скорректированным коэффициентом существуют различия (0,9%). Так как число наблюдений достаточно велико, то различия не столь существенны, и поэтому можно использовать R² и R для оценки тесноты связи. Множественный коэффициент корреляции (R = 0,946) свидетельствует об очень тесной связи между факторами и результатом, множественный коэффициент детерминации показывает, что 89,6 % вариации выручки связано с включенными в модель факторами. Полученные выводы следует оценить на достоверность: насколько они существенны для генеральной совокупности, поскольку мы получили лишь выборочные показатели связи и выборочное уравнение регрессии.

3. Дадим оценку значимости уравнения в целом, условного начала и коэффициентов чистой регрессии.

Оценка значимости уравнения в целом проводится на основе дисперсионного анализа. Предположим, что уравнение не значимо для генеральной совокупности (Н₀: 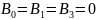). В качестве альтернативной гипотезы выдвинем предположение о значимости уравнения (Н_А: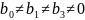 ). Проверим эти гипотезы на 5% уровне значимости. В качестве критерия выберем критерий F-Фишера, его фактическое значение определяется по формуле.

=

Фактическое значение критерия равно 115,76 (табл. 4.2.1). Сравним его с критическим значением 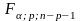, которое можно найти, используя встроенную функцию FРАСПОБР( ) или по таблице (приложение 4). В нашем случае: =FРАСПОБР(0,05;2;27)= 3,35.

Поскольку фактическое значение превышает критическое, принимаем гипотезу о значимости уравнения регрессии в целом для генеральной совокупности. Можно также оценить значимость критерия (фактического значения): из табл. 4.2.1 видно, что критерий значим уже при 5,682 ∙10^-14 %-ой области, что гораздо меньше принятой нами 5%-ой.

Следовательно, уравнение в целом значимо. Это означает тот факт, что в уравнении есть хотя бы один статистически достоверный параметр взаимосвязи, но возможно не значим какой-либо из его параметров для генеральной совокупности.

Выдвинем рабочую гипотезу о равенстве нулю всех параметров уравнения в генеральной совокупности и альтернативную ей:

H₀: H_A:

B₀ = 0; B₀  0;

B₁ = 0; B₁  0;

B₃ = 0. B₃  0.

Гипотезы проверим на 5% уровне значимости. Если выборка является малой, то для проверки гипотезы следует использовать критерий Стьюдента. Напомним, что найти его критическое значение можно, используя функцию СТЬЮДРАСПОБР(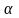 ;n-p-1) или данные таблицы в приложении 3 - 2,0518.

Фактические значения критерия t определяется по формуле: .

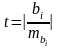EXCEL автоматически производит расчет фактических значений критерия t и его значимости, средних ошибок, доверительных интервалов (на 95%-ом уровне вероятности суждения) для каждого из параметров уравнения регрессии (табл. 4.2.1, последняя ее часть).

Все коэффициенты регрессии оказались достоверными: Р-значение ниже принятого уровня значимости. Следовательно, можно дать точечную и интервальную оценку параметрам в генеральной совокупности.

Точечная оценка позволяет предположить, что генеральное уравнение будет иметь параметры 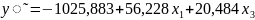при соответствующих размерах средних ошибок (табл. 4.2.2).

Табл. 4.2.2. Точечная оценка коэффициентов чистой регрессии.

Фактор	Выборочный коэффициент чистой регрессии (вi)	Стандартная ошибка (тв)
X1 - трудообеспеченность, чел./100 га.;	56,228	15,862
X3 - балл почвы;	20,484	2,058

Проведем интервальную оценку параметров:

.

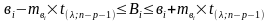Для нашей модели с уровнем вероятности суждения 95% можно утверждать, что параметры генерального уравнения множественной регрессии попадут в следующие интервалы (табл. 4.2.3).

Таблица 4.2.3. Интервальная оценка параметров регрессии

	Коэффициенты	Нижние 95%	Верхние 95%
Y-пересечение	-1025,883	-1385,82	-665,9475268
X1	56,228	23,68	88,7748150
X3	20,484	16,26	24,7061147

;

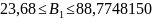Поскольку все коэффициенты чистой регрессии оказались значимыми, возможна их интерпретация. Учитывая, что выручка в расчете на 100 га с./х. угодий в базе данных дана в тыс. руб., коэффициенты чистой регрессии показывают, что:

- при увеличении трудообеспеченности на 1 человека/100 га, выручка в расчете на 100 га с./х. угодий увеличится в среднем на 56 228 руб., при условии, что все остальные факторы стоимости останутся неизменными и будут зафиксированы на среднем уровне (с уровнем доверия 95% можно утверждать, что в генеральной совокупности она может возрастать от 23 680 до 88 775 руб.);

- при увеличении значения балла почвы на 1, выручка в расчете на 100 га с./х. угодий в среднем будет возрастать на 20 484 руб. (с уровнем доверия 95% можно утверждать, что в генеральной совокупности она может возрастать от 16 260 до 24 706 руб.), при условии, что все остальные факторы останутся на среднем уровне;

Условное начало (у-пересечение) интерпретации не подлежит, поскольку нет случаев с нулевым значением всех перечисленных факторов.

4. Чтобы продолжить корреляционный анализ и сравнить факторы по силе влияния, определить чистый вклад каждого фактора рассчитаем стандартизованные коэффициенты (коэффициенты эластичности (Э) и бета-коэффициенты (β)) и коэффициенты раздельной детерминации (d²) по каждому фактору: 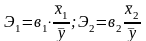и т.д.; и т.д.;

; и т.д., где 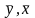- средние значения, 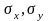- среднеквадратические отклонения факторного и результативного признака соответственно. Сумма коэффициентов раздельной детерминации дает множественный коэффициент детерминации: .

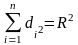Средние значения и среднеквадратические отклонения переменных определим с использованием встроенных статистических функций «СРЗНАЧ(…)», «СТАНДОТКЛОНП(…)».

Для определения коэффициентов раздельной детерминации нам понадобятся коэффициенты парной корреляции каждого из факторов с результативной переменной. Для этого воспользуемся матрицей парных коэффициентов корреляции с использованием инструмента «Корреляция» пакета анализа данных EXCEL (табл. 4.1.5).

Результаты расчетов стандартизованных коэффициентов регрессии и коэффициентов раздельной детерминации оформим (табл.4.2.4).

Табл. 4.2.4. Стандартизованные коэффициенты регрессии и коэффициенты раздельной детерминации

Переменная	Коэффициент чистой регрессии, b	Среднее значение	Среднеквадратическое отклонение, σ	Коэффициент парной корреляции с зависимой переменной, ryx	Коэффици-ент эластич-ности, Э	Бета-коэф-фициент, β	Коэффи-циент раздельной детерминации, d2
X1 - трудообеспеченность, чел./100 га.;	56,228	5,43	4,21	0,72	0,237	0,271	0,1951
X3 - балл почвы;	20,484	98,00	32,46	0,92	1,560	0,762	0,7010
У - выручка в расчете на 100 га с./х. угодий, тыс. руб.	х	1286,85	872,50	1	х	х	х
Итого	х	х	х	х	х	х	0,896

Коэффициент эластичности (Э₄) показывает, что при увеличении трудообеспеченности, чел./100 га. на 1% (от среднего уровня) размер выручки в расчете на 100 га с./х. угодий возрастет на 0,237%, при условии, что прочие факторы будут зафиксирована на среднем уровне.

Э₅ показывает, что при увеличении балла почвы на 1% размер выручки в расчете на 100 га с./х. угодий возрастет на 1,56% от ее среднего уровня (при неизменности прочих факторов).

-коэффициенты показывают, что если каждый из факторов изменится на свое среднеквадратическое отклонение, то размер выручки в расчете на 100 га с./х. угодий под воздействием трудообеспеченности, чел./100 га. возрастет на 0,27 своего среднеквадратического отклонения, за счет балла почвы – на 0,76.

Коэффициенты раздельной детерминации показывают вклад каждого фактора в формирование коэффициента множественной детерминации, вклад первого фактора – 19,51%, второго – 70,10%. Сумма частных коэффициентов равна коэффициенту детерминации: .

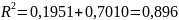Итак, при анализе стандартизованных коэффициентов регрессии и коэффициентов раздельной детерминации было выявлено, что на величину выручки в расчете на 100 га с./х. угодий влияние различий в баллах почвы сильнее, чем различия в трудообеспеченности, чел./100 га.

5. Следует отметить, что модель можно использовать в целях прогнозирования, поскольку при высоком коэффициенте детерминации параметры уравнения регрессии оказались значимы.

Определим прогнозное значение выручки в расчете на 100 га с./х. угодий. Предположим, что мы хотели бы получить выручку со следующими параметрами: трудообеспеченность, чел./100 га – 6,8 чел./100 га, балл почвы – 2756.

Подставим прогнозные значения факторов в уравнение регрессии, тогда прогнозная стоимость составит: =-1025,883+56,228∙6,8+20,484·2756=55810,37 (тыс.руб.)

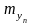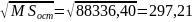Средняя ошибка прогноза ( ) зависит от среднеквадратического отклонения индивидуальных значений от выравненных по уравнению регрессии: S_ост.= (см. табл. 4.2.1) и ошибки положения плоскости регрессии при экстраполяции факторных признаков (расчет этой ошибки производится с применением линейной алгебры, что не входит в программу дисциплины). Доверительный интервал прогноза имеет вид:

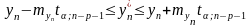
Если в качестве приблизительной оценки взять S_ост, то 95% доверительный интервал прогноза составит (без учета ошибки положения плоскости регрессии):

55810,37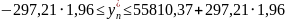 582,5316

Прогнозное значение стоимости квартиры заданных параметров в генеральной совокупности при уровне вероятности суждения 95% будет находиться в пределах от 55227,84 до 56392,90 тыс. руб.