4.2 задача

Вариант 27

Задача 2. Определение индекса цен

Пример 1. Определение агрегатного индекса цен.

Известны данные об уровне цен на продукцию растениеводства за отчётный и базисный годы, а также объём реализации продукции за отчётный год (табл. 1).

Табл. 1. Объём и цены реализации продукции

Продукция	Исходные данные			Расчётные данные
	Объём реализации в отчётном году, т	Цена реализации, тыс. руб. за 1 т.		Стоимость реализованной продукции, тыс. руб.
		базисная	отчётная		отчётная	условная
	q1	р0	р1		q1 р1	q1 р0
Зерно	20	0,23	0,34		6,8	4,6
Картофель	3	0,82	0,91		2,73	2,46
Капуста	11	0,91	1,12		12,32	10,01
Итого	Х	Х	Х		21,85	17,07

Требуется: определить среднее изменение цен по всей совокупности рассматриваемых продуктов.

Методические указания. Изменение цен в отчетном году по сравнению с базисным по отдельным видам продукции оценивается путем расчета индивидуальных индексов (в динамике – коэффициентов роста) . Для оценки среднего изменения цен по всей совокупности необходимо рассчитать сводный индекс цен. В силу несопоставимости индивидуальных индексов, рассчитанных к разной базисной величине, простое их осреднение, как и в задаче 1, неприемлемо. Необоснованно экономически также простое суммирование цен р₀ и р₁ , хотя они имеют одну и ту же единицу измерения, но относятся к различным, несопоставимым объемам реализованной продукции. Значение одного и того же изменения цен в совокупности не одинаково, оно тем выше, чем больше реализуется данного вида продукции. Для приведения данного уровня цен в сопоставимый вид учитывают степень их распространения в совокупности через объем реализации q_1. При этом объем реализации берется один и тот же, в итоге получают агрегаты с разными ценами и . Тогда индекс цен составит .

Это агрегатный индекс постоянного (фиксированного) состава, то есть с одним и тем же набором и объемом продукции. Он может быть общим или групповым в зависимости от задачи анализа. Индексируемой величиной здесь является цена р_i, а количество продукции q_i выступает в качестве веса для цен. Следует обратить внимание на то, что для признаков продукции – цен с одинаковыми единицами измерения - употребляется понятие веса в отличие от коэффициентов соизмерения для физического объема несопоставимых и с разными единицами измерения продуктов (см. задачу 1).

Индексы цен, как и индексы других качественных показателей (урожайности, себестоимости, доходности, зарплаты, трудоемкости и т.д.) рассчитываются при весах отчетного периода q₁, не базисного q₀. Это обусловлено в первую очередь экономическим значением индекса. При весах q₁ разность между числителем и знаменателем 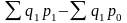тыс. руб. показывает, с одной стороны, увеличение выручки продавцов продукции за фактически реализованный ее объем q₁, а, с другой – увеличение расходов покупателей на реально приобретенный объем продукции q₁. При весах q₀ разность показывала бы изменение выручки продавцов и расходов покупателей от изменения цен для продукции прошлого года. Такой расчет возможен теоретически, но он мало актуален практически, поэтому применяется веса отчетного периода q₁:

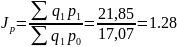
Вывод. Цены реализации продукции для данной сельскохозяйственной организации возросли за анализируемый период в 1,28 раза, или на 28%. Выручка от реализации продукции увеличилась за счет роста цен на 4,78 тыс. руб. ( ).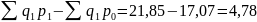

Пример 2. Расчет индекса цен по формуле средней гармонической.

Имеются данные о стоимости реализованной продукции в отчетном периоде и индивидуальных индексах цен по разнородной продукции (табл. 2).

Требуется определить общий индекс цен по сравнению с базисным годом.

Табл. 2. Стоимость реализованной продукции и изменение цен

на продукты

Продукция	Исходные данные			Расчётные данные
	Стоимость реализованной продукции в отчётном году тыс.руб.	Индивидуальный индекс цены		Условная стоимость продукции отчётного года в ценах базисного года, тыс. руб.
	q1p1
зерно	6,8		1,48	4,6
картофель	2,73		1,11	2,46
капуста	12,32		1,23	10,01
Итого	21,85	Х		17,07

Для расчёта индекса цен необходимо вычислить, как показано в примере 1 данной задачи, два агрегата - и . В данном примере величины q₁p₁ являются исходными данными, а для расчета величины q₁p₀ значения q₁ и p₀ неизвестны. Но при известных индивидуальных индексах цен величину p₀ можно определить как , тогда стоимость продукции q₁p₀ можно рассчитать как . В итоге формула расчета индекса цен преобразуется I_p = .

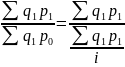Это средний гармонический индекс, идентичный по величине агрегатному индексу цен фиксированного состава. В задаче он равен I_p 21,85/17,07 = 1,28.

Вывод. Мы убедились в том, что формула средней гармонической приводит к тому же результату, что и формула агрегатного индекса цен: цены на рассматриваемую продукцию возросли за анализируемый период в 1,28 раза, или на 28%. Выбор способа расчёта определяется характером имеющейся информации.

Следует иметь в виду, что в случае, когда известна не стоимость продукции q₁p₁, а её структура в виде долей , то расчёт общего индекса при наличии данных об индивидуальных индексах цен проводится по формуле I_p = .
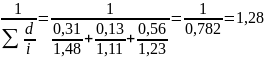