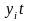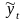3.2 задача

Задача 2. Выравнивание динамического ряда по способу наименьших квадратов.

Имеется динамический ряд поступлений доходов в муниципальный бюджет Ростовской области по земельному налогу за 7 лет (табл.1). Информация найдена на официальном сайте Федеральной налоговой службы https://www.nalog.ru/rn61/related_activities/statistics_and_analytics/forms/ .

Табл. 1. Динамика поступлений земельного налога в муниципальный бюджет Ростовской области, млрд. руб.

Год	№ года	Земель- ный налог, млрд. руб.	Расчётные данные
			произведе- ние уровня земельного налога на номер года	квадрат номера года	выровнен- ный уровень земельного налога, млрд.руб.	отклонение фактичес- кого уров- ня от выравнен- ного, млрд. руб.
	t	yi		t2
2013	1	16,52	16,52	1	17,3	-0,78
2014	2	16,76	33,52	4	17,86	-1,10
2015	3	20,11	60,27	9	18,42	1,69
2016	4	19,72	78,88	16	18,98	0,74
2017	5	19,94	99,7	25	19,54	0,40
2018	6	20,45	122,7	36	20,1	0,35
2019	7	19,36	135,52	49	20,66	-1,3
Итого:	28	132,86	547,11	140	132,86	0

Требуется: определить тенденцию поступлений от земельного налога, используя метод наименьших квадратов, оценить пригодность тренда для прогнозирования, выполнить прогноз поступлений в бюджет на 2020 год.

Важнейшей задачей анализа динамических рядов является выявление основной тенденции, то есть направления и характера изменения признака во времени. В ряде случаев тенденция четко выражена и не требует выявления. Задача сводится к описанию тенденции в виде математической функции, но чаще всего исследователь имеет дело с рядами, в которых тенденцию выявить достаточно сложно в силу колебания уровней ряда.

Чтобы ответить на вопрос, почему в одних случаях тенденция проявляется чётко, а в других – нет, следует уяснить, под влиянием каких факторов формируется каждый уровень ряда.

На каждый уровень ряда (у) влияет много различных факторов, которые можно объединить в 3 группы:

- факторы, постоянно воздействующие на уровни ряда. Эти факторы определяют тенденцию развития. Например, инфляционные процессы в экономике ведут к систематическому повышению цен;

- факторы, периодически воздействующие на уровни ряда. Эти факторы определяют устойчивые колебания уровней во времени. Колебания могут возникать в течение года (так называемое явление сезонности) или в течение более длительного периода, свыше года (так называемое явление цикличности). Факторы, которые вызывают явления сезонности и цикличности, называются факторами сезонности и факторами цикличности.

- случайные факторы, воздействующие на уровни ряда без какой-либо закономерности, в случайном порядке. Они действуют хаотично, вызывая вариацию (изменчивость) уровней ряда.

Действуя одновременно, факторы определяют величину признака в каждый конкретный промежуток времени. Если влияние факторов сезонности, цикличности и случайных факторов велико, то тенденция развития не проявляется четко. На рисунке 1 видно, что в рассматриваемой задаче уровни динамического ряда не имеют однозначной тенденции. Так, в 2016 и 2019 годах наблюдается спад поступлений от налога по сравнению с предшествующими годами, в другие же периоды – рост. Тенденция к росту уровней ряда по прямой линии «затушевана» влиянием других факторов. Для выявления чёткой тенденции необходимо устранить влияние прочих факторов, кроме факторов тенденции. С этой целью в статистике разработаны методы выравнивания динамических рядов.

В основе методов положено свойство средних величин отражать типические черты признака при обобщении индивидуальных значений. Осреднение может быть как непосредственно по уровням ряда, так и по показателям динамики – абсолютному приросту, коэффициенту роста и т.п. В зависимости от характера осреднения методы выравнивания объединены в две группы – методы механического выравнивания (метод укрупнения периодов, метод скользящей средней) и методы аналитического выравнивания на основе математических функций (по среднему абсолютному приросту, по среднему коэффициенту роста, метод н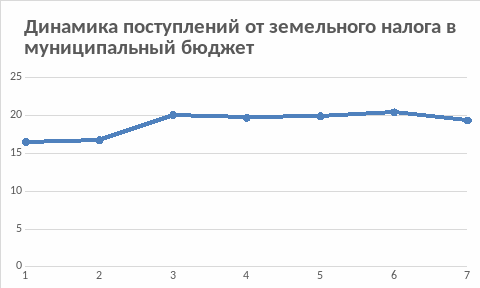 аименьших квадратов).

Рис.1.

Выравнивание ряда динамики способом наименьших квадратов состоит в отыскании уравнения кривой, которая наиболее точно отражала бы основную тенденцию изменения уровней ряда в зависимости от времени t. Параметры уравнения при этом находят, исходя из требования, чтобы рассчитанные значения были максимально приближены ко всем эмпирическим данным, а сумма квадратов отклонений фактических уровней от их значений, исчисленных по найденному математическому уравнению, была минимальной, то есть 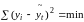, где у_i – фактические уровни динамического ряда, 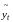– уровни, вычисленные по уравнению.

Этот способ выравнивания, как и другие приёмы, следует применять в сочетании со способом укрупнения периодов. Выявление тенденции развития методом наименьших квадратов следует проводить, как правило, внутри качественно однородных периодов.

Выравнивание производится с помощью различных математических функций – линейной, показательной, логарифмической, параболы разных порядков и др. Выбор функции проводится на основе теоретического анализа изучаемого явления, применения графического метода, использования скользящих средних и других приемов.

Для оценки общей направленности изменения и формы кривой целесообразно использовать графический метод. Анализ графика (рис. 1.) свидетельствует о том, что наблюдается общая направленность изменений к росту уровней, и по форме она близка к линейной.

В этом случае эту тенденцию можно выразить уравнением прямой линии , где t – № года, 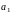– среднегодовой абсолютный прирост, рассчитанный с учётом его величины за все годы рассматриваемого периода, 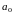– выровненный, свободный от случайных колебаний исходный уровень ряда при t = 0.

Для определения двух параметров уравнения а₀ и а₁ в соответствии с требованием метода наименьших квадратов строится система из двух нормальных уравнений. Первое уравнение получают умножением исходного уравнения 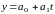на коэффициент при а₀, равный 1, и суммированием произведений по всем наблюдениям. В итоге получаем . Второе уравнение находится аналогично: все члены исходного уравнения умножаются на коэффициент при втором неизвестном а₁, то есть на величину t, и произведения суммируются: . Следовательно, система нормальных уравнений для прямой будет иметь вид:

Если число неизвестных параметров больше 2, например, при решении уравнения параболы 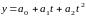, то подобным образом составляется система из трёх или больше нормальных уравнений.

Для определения параметров а_о и а₁ в систему приведённых выше уравнений подставляют суммы признаков 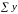и , сумму их произведений 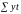и сумму квадратов номеров лет :

132,84 = 7a₀+28a₁

547,11 = 28a₀+140a₁

Выровняем коэффициенты при а₀, разделив первое уравнение на число лет n=7, а второе на :

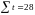18,98 = а₀ + 4а₁

19,54 = а₀ +5а₁

Вычтем из второго уравнения первое и определим значение а₁:

0,56 = а₁

Подставим а₁ = 0,56 в одно из уравнений и рассчитаем значение а₀:

18,98 = а₀ + 4×0,56; а₀ = 16,74.

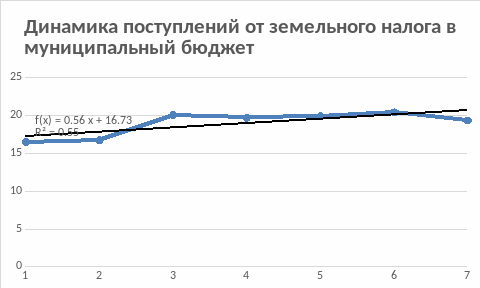Таким образом, уравнение для выравнивания динамического ряда имеет вид: y_t = 16,74 + 0,56t. Такое уравнение называют трендом. Оно показывает, что в среднем каждый год поступления от земельного налога в муниципальный бюджет увеличивались на 0,56 млрд. руб., начиная с выровненного исходного уровня 16,74 млрд. руб.

Рис. 2

Выровненные (сглаженные) уровни получают, подставляя в уравнение номера лет t. Для 2013 г. при t = 1 выровненный уровень составит 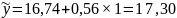млрд. руб., для 2015 г. при t=3 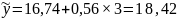млрд. руб. и т.д.

Достоинством метода наименьших квадратов по сравнению с другими приемами выравнивания рядов динамики является учёт значений всего ряда, а не только крайних уровней или взятых для расчёта скользящих средних. При этом абстрагируются от всех случайных колебаний и получают выровненные значения для всего ряда, показанные в табл.1. и на рис.2.

Для оценки степени приближения выровненных уровней к фактическим необходимо найти их разность , а также остаточную дисперсию:

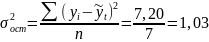
Среднее квадратическое отклонение 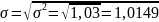млрд. руб., а коэффициент случайной вариации по отношению к среднему уровню составляет .

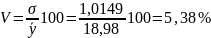Коэффициент детерминации (аппроксимации) R²=0,55 говорит о том, что 55% общей вариации исходных уровней ряда сформированы общей тенденцией, и 45% - случайными и цикличными (если они есть) факторами.

Средний уровень случайной вариации позволяет использовать уравнение тренда в целях прогнозирования. Следует, однако, учесть, что прогнозирование по тренду целесообразно при условии сохранении действующих факторов тенденции в ближайшем будущем (в нашем случае, например, при сохранении действующих законов по налогообложению). Для расчёта прогнозного уровня временного ряда нужно подставить в уравнение тренда порядковый номер прогнозного года. Рассчитаем прогнозное значение поступлений налогов в бюджет для 2021 года (t=9):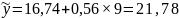 млрд. руб.

Средняя ошибка прогноза по линейному тренду составит:

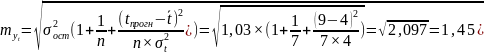млрд. руб.

При 5%-ом уровне значимости критическое значение критерия Стьюдента составит 2,57. Следовательно, предельная ошибка прогноза составит 1,45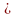 2,57=3,73 млрд. руб. Таким образом, с 95%-ым уровнем вероятности мы можем гарантировать, что поступления в муниципальный бюджет от земельного налога в 2021 году будут не ниже 18,05 млрд. руб. (21,78-3,73) и не выше 25,51 млрд. руб. (21,78+3,73).